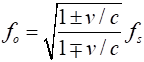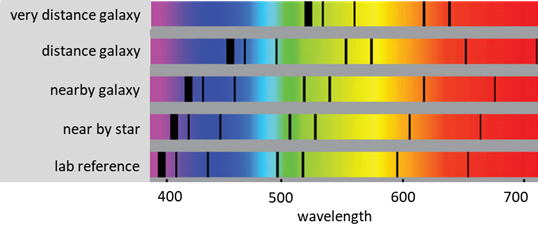|
SPECIAL RELATIVITY DOPPLER EFFECT FOR LIGHT DETECTING MOTION IN THE UNIVERSE HUBBLE’S LAW
|
|
SUMMARY The
relativistic
Doppler effect is the change in
frequency (and wavelength) of light, caused by the relative motion of the
source and the observer considering the effects described by the special
theory of relativity. The
relativistic Doppler effect is different from the non-relativistic Doppler
effect as the equation includes the time dilation effect of special
relativity and does not involve the medium of propagation as a reference
point. The
velocity of a star w.r.t. the Earth can be estimated by the redshift
or blueshift
in its observed spectrum. |
|
MOTION IN THE UNIVERSE Stars and interstellar gas are bound by gravity to form
galaxies, and groups of galaxies can be bound by gravity in galaxy
clusters. Except for stars in the
Milky Way and the galaxies in the Local Group, almost all galaxies are moving
away from us due to the expansion of the universe. This motion of stellar
objects can be determined by looking at their spectrum. Because of the
Doppler effect, objects moving towards us are blueshifted, and objects moving away are redshifted. The wavelength of redshifted light is longer, appearing redder than
the source and the wavelength of blueshifted
light is shorter, appearing bluer than the source light.
A redshifted absorption or emission line will appear
more towards the red end of the spectrum than a stationary line. Conversely,
a blueshifted
absorption or emission line will appear more towards the blue end of the
spectrum. DOPPLER EFFECT FOR LIGHT We have studied the Doppler Effect for sound in Module 3.1. A
change in frequency of the sound detected occurs when there is relative
motion between the source and the observer. For sound, the speed of
propagation for the wave is relative to the medium through which the sound is
propagating. But for light, there is no medium. It is possible for the source of sound
to travel fast than the speed of the sound wave. But, this is not possible
for light. So, the Doppler Effect for sound is different to the Doppler
effect for light. The equation describing the Doppler Effect for light is (1) where v is the magnitude of the relative velocity
of source (s) and observer (o). The magnitude v is a positive number. If the source and receiver are
approaching, then the frequency increases The spacing of the energy levels is unique
to the atom, so an atom absorbs and emits light of characteristic frequencies
due to the quantized energy levels. Scientists have observed these
characteristic frequencies in the light from stars and this makes it possible
to identify atoms and molecules in distance stars and galaxies. The spectrum
from stars are often shifted due to there relative
motion w.r.t the Earth.
Fig. 1. Absorption lines in the visible
spectrum showing the shift in frequency due to motion of the source.
Molecules absorb energy at discrete frequencies which are unique to the atoms
that constitute the molecules. One reason for the shift in frequencies is
the relativistic Doppler Effect and the shift in frequencies are used to
estimate the speed of the emitting objects with respect to us. This is the
source of the well-known redshifts in the light from stars caused by them
moving away from us. The redshifts provide us with evidence of an expanding
universe. The farther away a star, the greater the redshift. This led to H.
Shapley and E. Hubble to conclude the origin of the universe started with a Big
Bang.
Also, the relativistic Doppler Effect is used to find the astronomic
distances of objects such as quasars (objects that have enormous masses and
emit incredibly amounts of radiation).
Fig. 2. The redshift of the light from
distance astronomical objects. The redshift is used to estimate their
distances from us. Edwin Hubble would later use this
information, as well as his own observations, to define Hubble's law: The further a galaxy is from
the Earth, the faster it is moving away from us. Hubble's law can be
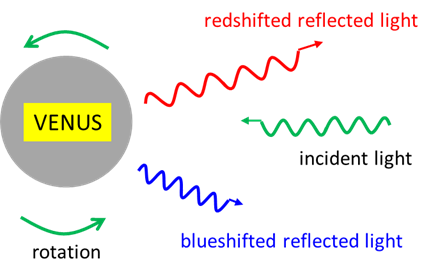
generalised to where v is the velocity, Venus rotates in the opposite direction to
the spin of the Earth. This was found by observing sunlight reflected from
the surface of Venus – one side the light is redshift and on the other it is blueshifted. The same technique is used to study the
rotation of stars.
Fig. 3. The relativistic Doppler Effect
is used to study the rotations of planets and stars. Australian Telescope National
Facility Translational Motion:
If the spectral lines in a star's spectrum are uniformly redshifted this would
indicate relative recessional motion between the observer and the star. The
amount of redshift would depend on the recession velocity. A complicating
factor is the fact that the motion may not be directly away from us. In this
case the Doppler shift of lines would depend on the component of velocity
away from us, that is the star's radial velocity. A star moving towards us
would, of course, exhibit a blueshift in its spectral lines. Rotational Motion:
Even though we can still only resolve most stars as point sources they are in
fact large, roughly spherical balls of hot gas and plasma. Stars rotate, that
is they spin on their axis. The Sun's sidereal rotational period is about 26
days on the solar equator and possibly up to 36 days at the poles. The
different rates are since it is not a solid sphere and the gas and plasma can
rotate at different speeds. If we obtain a spectrum from a distant star that
is rotating in the same plane as us, then the light gathered is a combination
of light from across the disc of the star. As part of the star appears to
rotate towards us its light will be blueshifted.
The light from the part of the star rotating away from us will be redshifted.
The section in the middle of the disc that is moving tangentially to us will
not exhibit Doppler-shift. What
effect will this have on the star's spectrum? The
net effect is that the star's spectral lines will appear smeared out. This
broadening of lines can be distinguished from the effects of pressure
broadening due to stellar pressure. The beauty of rotational broadening is
that it can be used to measure the rotation rate of stars. As with translational
velocity the alignment of the plane of rotation of the star with Earth is a
factor and must be calculated from the spectrum. |
|
|