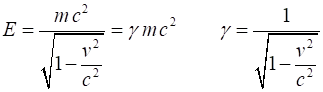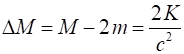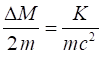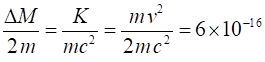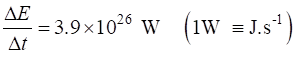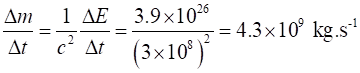|
LIGHT and SPECIAL
RELATIVITY EQUIVALENCE OF MASS AND ENERGY |
|
SUMMARY Conservation of mass-energy The
total mass-energy of an isolated system is a conserved quantity
Relativistic energies: rest energy Rest energy When an object is at rest Total energy
total energy = rest mass energy + kinetic energy + potential energy
Total energy E of a single object of mass m moving with speed v
Kinetic
energy
The
binding
energy EB is the work
(energy) required to pull the particles out of a bound system into separate
free particles at rest. The
mass
defect |
|
EQUIVALENCE OF MASS AND ENERGY The equation (1) is
one of the most famous equations in physics. Even when an object has zero
velocity (zero kinetic energy), the object still has energy through its mass.
Nuclear reactions are proof that mass and energy are equivalent. In
classical physics, we had the laws of conservation of mass and conservation
of energy. We must modify these laws as mass and energy are connected. These
two laws are combined into a single law, the law of conservation of mass-energy. Even
though we often say “energy is turned into mass” or “mass
is converted to energy” or “mass and energy are
interchangeable”, you must understand we mean that mass and energy
are actually equivalent. Mass is
simply another form of energy, and we can use the terms mass-energy and
energy interchangeably. |
|
Example 1 When
you compress a spring between your fingers, does the mass of the spring (a)
increase, (b) stay the same, or (c) decrease. Justify your answer. Solution
When
the spring is compressed by an amount s, the potential energy is increased by This is a very strange result.
The mass of the particles that constitute the spring (electrons, protons,
neutrons) do not increase. The increase in mass of the spring is simply due
to the increase in the energy due to the increase in energy associated with
the interaction of the particles that make the spring. This reasoning is
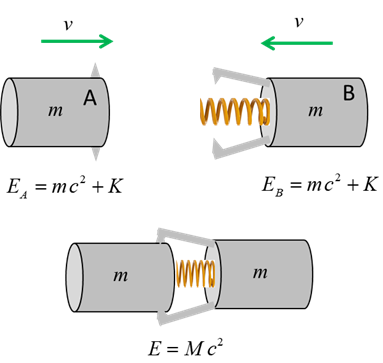
explained in the following example. Consider
two blocks, each of mass m (m is an invariant quantity) and kinetic energy K moving towards each other. A
spring placed between them is compressed and locked into place after they
collide. We can investigate the elastic collision by applying the law of
conservation of mass-energy.
The
energy before the collision is
The energy after the elastic collision
where
M is the mass
of the system of two block and spring joined together. Applying
the law of conservation of mass-energy
The new mass M is
greater than the sum of the individual masses of the two blocks
So, kinetic energy has been converted into mass. The
result being that the potential energy of the spring has caused the system to
have more mass. The increase in mass is
The
fractional increase in mass in this example is very small If we take m =
0.1 kg and v = 10
m.s-1, and putting in the numbers It is OK to use the classical equation for the kinetic
energy since This example shows that the increase in mass for
macroscopic systems is so small that the mass increase can be neglected.
However, this is not true for nuclear systems. |
|
Mass Defect and
Binding Energy The
equivalence of mass and energy becomes apparent when we study the binding
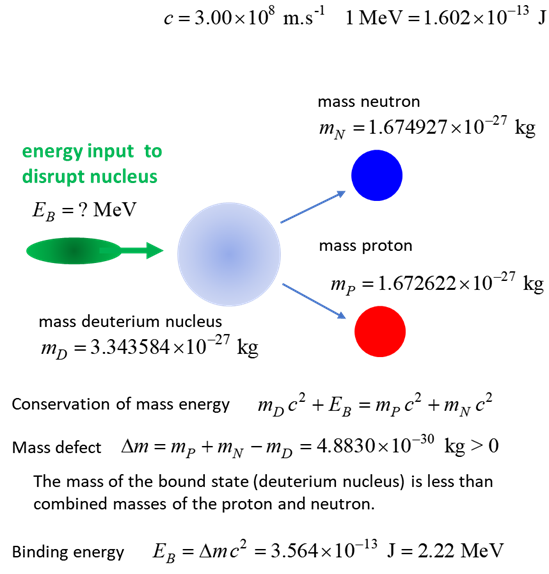
energies of systems like nuclei and atoms. For example, a deuteron is a
proton and a neutron bound by the strong nuclear force. The binding energy EB is the work (energy) required to pull the particles out of the
bound system into separate free particles at rest. Let
a deuteron nucleus at rest be the initial state Total
energy Ei of the initial bound state of
the deuteron (mass mD )
The
total energy Ef of the final state
is equal to the sum of the rest energies of the free proton and free neutron
(masses mP and mN )
The
mass defect is The
binding energy is
Think
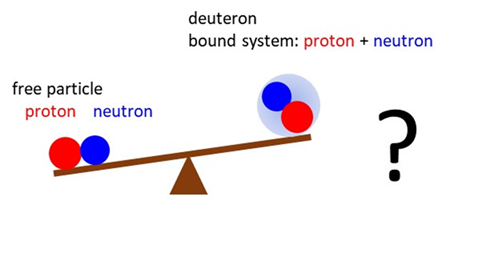
of what we have just considered. The mass of the proton and neutron are
invariant. The deuteron is simply the proton and neutron bound together. But
the mass of the deuteron is less than the sum of the masses of the proton and
neutron.
From
a common-sense point of view or from the principles of classical physics this
cannot be true!!! The natural
world as explained by the concepts of modern physics are bizarre. So, you
need to apply the principles of modern physics and not use our everyday
experience in forming metal models. To explain why the bound state has less
mass than the sum of the constituent particles, we need to consider the
concepts of relativistic energies more carefully.
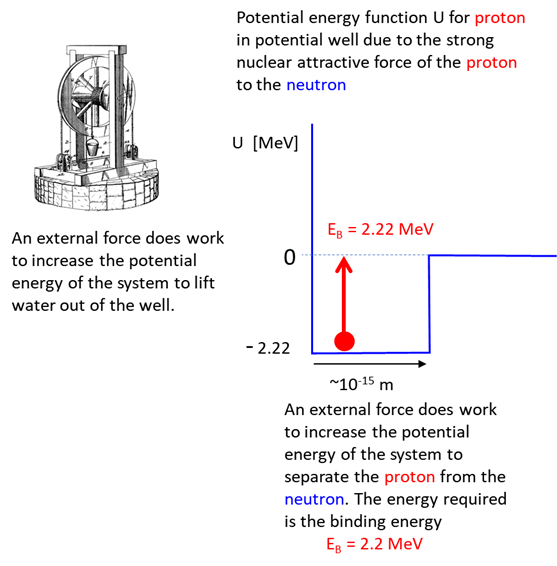
Rest mass
energy Kinetic
energy Potential
energy of system
Total
energy Bound
state: deuteron where Free
particle state: proton and neutron Conservation
of mass-energy Hence, the mass of
the deuteron is less than the mass of its constituent particles (proton +
neutron) because of the negative contribution from the potential energy Review Nuclear binding energy is the minimum energy that would be required to disassemble the
nucleus of an atom into its component parts. These component parts are
neutrons and protons, which are collectively called nucleons. The binding is
always a positive number, as we need to spend energy in moving these
nucleons, attracted to each other by the strong nuclear force, away from each
other. The mass of an atomic nucleus is less than the sum of the individual
masses of the free constituent protons and neutrons, according to Einstein's equation The
term nuclear binding
energy may also refer to the energy balance in processes in
which the nucleus splits into fragments composed of more than one nucleon.
The process when light nuclei combine is called nuclear fusion and the splitting of heavy nuclei into lighter
ones is called nuclear fission. Either process can result in release
of this binding energy. These nuclear binding energies and forces are on the
order of a million times greater than the electron binding energies for
chemical reactions. |
|
Exercise
2
Combustion of petrol A
car burns petrol to make a car move. In a journey, a car used 100 L of
petrol. What is the decrease in mass of the petrol consumed? Every
1 kg of petrol used releases an energy of 43.6 kJ Density
of petrol is 750 kg.m-3 Solution 1st
step is to find the mass
of petrol used: 1000 L = 1 m3 100 L =
0.1 m3 1 m3 2nd
step is to find the energy
released 1 kg 3rd
step is to find the decrease in mass of
the petrol
You would need a good balance to measure the change in mass of
the petrol resulting from the combustion of petrol with oxygen. So, it is not
possible to measure any change in mass that occur in chemical reactions.
However, this is not the case for nuclear reactions. |
|
Exercise
3 Production of
energy by the Sun The
rate at which energy reaches the Earth's surface from the Sun, is called the solar constant. Its value is approximately equal to
1388 W.m-2. Use the values of the solar constant and the distance
between the Earth and Sun to estimate the rate at which energy is emitted by
the Sun and the corresponding decrease in the Sun’s mass.
Solution Assume that the Sun radiates uniformly
in all direction. The energy emitted from the Sun passes through a spherical
surface area A of radius The
rate P at
which the energy passes this spherical surface is Therefore, the rate at which energy is radiated from the
Sun is The
corresponding rate of decrease in mass of the Sun is The
loss in mass of the Sun is equivalent to three times the mass of the Queen
Mary every second.
The
Sun loses a rather a large amount of energy each second. Since the mass of
the Sun is 1.99x1030 kg, the loss in mass each year is small. Even
after 1.5x109 years (1.5 billion years), radiating at its present
rate, the Sun would lose a mere 0.01% of its mass. The Sun will not evaporate
away in our lifetime. |
|
Example 4
A chemical reaction Two
oxygen atoms attract each other and can unite to form the O2 molecule
with the release of energy (A) What
is the difference in mass between the two oxygen atoms and the oxygen
molecule? (B) If
1.00 g of O2 was formed by this chemical reaction, what would be
the total loss in rest mass and what is the total energy released? mass of O2 molecule
is about 5.3x10-26 kg Solution (A)
The
decrease in mass is extremely small in a chemical reaction. (B) Number
of O2 molecules in 1.00 g (1.00x10-3 kg) of oxygen Mass
loss in the formation of 1.00 g (1.00x10-3 kg) oxygen Energy
released in the formation of 1.00 g (1.00x10-3 kg) oxygen While
the mass loss is exceedingly small, the total energy released however, is
large. This is because of the conversion factor |
