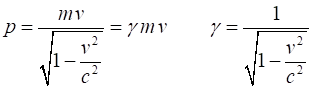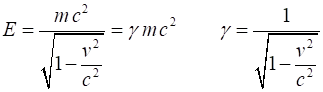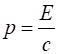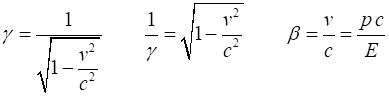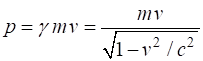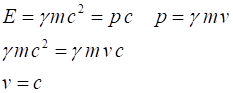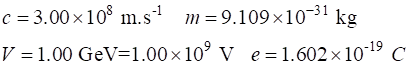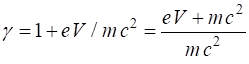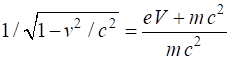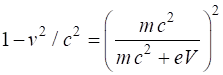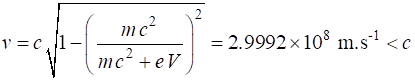|
LIGHT and SPECIAL
RELATIVITY RELATIVISTIC ENERGIES |
|
SUMMARY Einstein’s
1st postulate states that the laws of physics are the same for all
observers in all inertial frames of reference. So, the laws of conservation
of momentum and energy applied to isolated systems must be valid in all
inertial frames of reference. The mass m of
a single object is taken as an intrinsic property of the object and is now
considered an absolute
quantity. The velocity Relativistic momentum
Relativistic energies: rest energy Rest energy When an object is at rest Total energy energy of a single object of mass m moving with speed v
Kinetic
energy
Photon
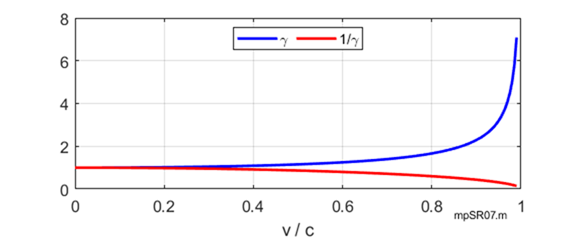
Relativity factors gamma
|
|
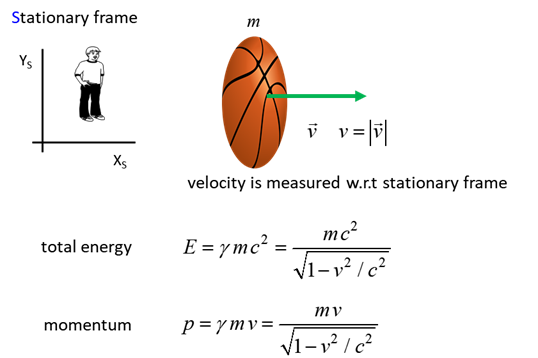
RELATIVISTIC ENERGIES Einstein’s 1st postulate states that the laws of physics are the same for all observers in all inertial frames of reference. So, the laws of conservation of momentum and energy applied to isolated systems must be valid in all inertial frames of reference. What is the energy of a single moving object?
The mass m of a single object is taken as an intrinsic property of
the object and is now considered an absolute quantity. The velocity The momentum
p of a
single object of mass m and
speed v is
(1) The total energy E of a single object of mass m and
speed is
(2) Equation 2 applies to any single object, for example,
electron, proton, atom, molecule, basketball, star. Equation 2 implies that even at rest the object
(3) This rest energy can be converted into other forms such as
kinetic energy or electromagnetic energy. When an object is not at rest, we
can think of its total energy (4) Thus, the kinetic energy K of
the object is always a positive quantity and is given by equation 5 (5) When At
slow speed v << c, the kinetic energy is approximately equal to that given by the
classical equation for the kinetic energy (6) We
can show that equation 6 is valid using the binomial
approximation to express the factor
There
are four parameters m, v, p and E that characterize the motion of an object. We can derive a
useful expression for E in terms of p and m (7) (8) Equation
7 is an important equation since linear momentum p is a more fundamental concept than kinetic energy. There is no
conservation law of kinetic energy, whereas the law of conservation of linear
momentum is inviolate as far as we know.
Rest energy of an electron Rest energy of a proton PHOTON The photon is a type of elementary particle, the quantum
of the electromagnetic field including electromagnetic radiation such as
light, and the force carrier for the electromagnetic force. The mass of the
photon is zero total energy of a
photon
Linear momentum
photon
The energy of a photon is completely due to its motion, and not
at all to its rest energy Any
particle with zero mass |
|
Example 1 Show that a particle of zero mass propagates at the speed of
light. Solution |
|
Example 2 An electron is accelerated from rest by an electrical potential
difference of 1.00 GV. What is the final velocity of the electron? Solution The accelerating voltage increases the kinetic energy of the
electron
We cannot use the classical expression for kinetic energy. The electron is accelerated to almost the speed of light. You will
notice that relativistic calculations are more involved than their classical
equivalent calculations. |