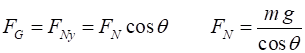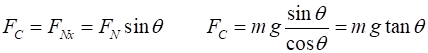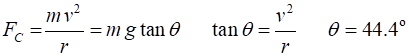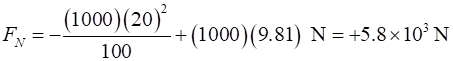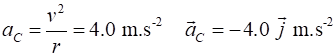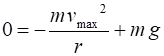MODULE 5
ADVANCED MECHANICS
CARS: CURVES AND BUMPS
|
An example of
centripetal force occurs when a car rounds a curve. If the wheels of the car
are rolling normally without slipping or sliding, the bottom of the tyre is
at rest with respect to the road at each instant. So, a frictional force
between the tyre and road corresponds to the centripetal force necessary for
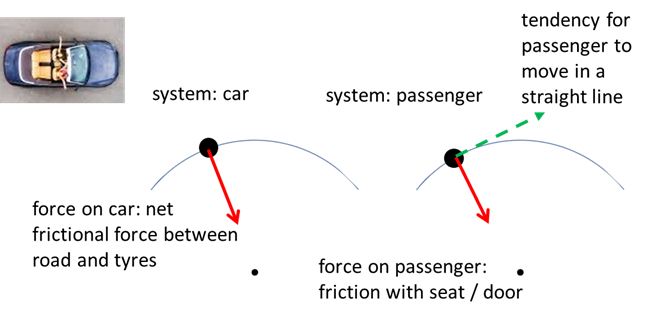
the car to travel in the curved path. When you are in
a car that travels quickly around a bend, you fell that you are thrust
outward. The car rounds the curve because of the frictional force between the
car tyres and the road. This is the centripetal force. But Newtons first law
applies to you in the car. You tend to move in a straight line. A frictional
force between you and the seat or the car door must be exerted on you so that
you also follow the curved path.
|
|
Example Consider a 1200 kg car rounding a
banked curve which has a radius of 65.0 m. Determine the banking angle of the
curve if the car travels around the curve at 25.0 m.s-1
without the aid of friction. Solution
For
the car to move in a circular path, there must be a force acting on it in the
+X direction towards the centre of the circle. Forces
in Y direction Forces
in X direction Centripetal
force Note:
Banking angle is independent on the mass
of the vehicle. Banking angle increases with increasing
speed. Banking angle decreases with increasing radius of the turn. |
|
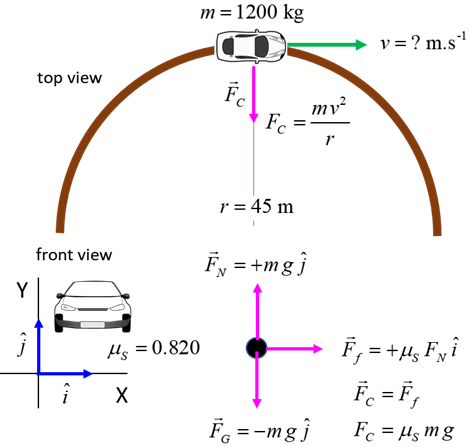
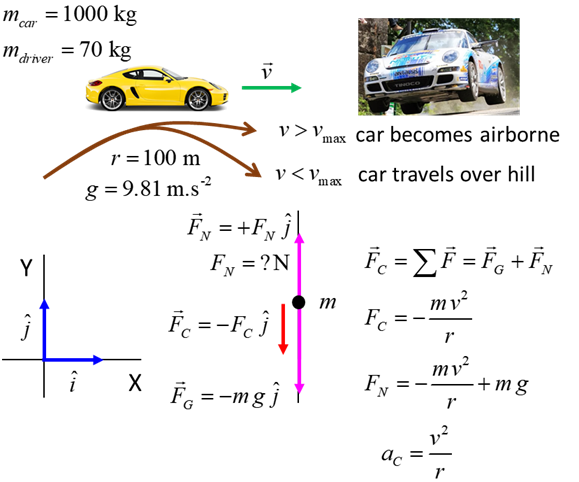
Example A person with a mass of 70 kg is
driving a car with a mass of 1000 kg at 20 m.s-1 over the
crest of a round shaped hill of radius 100 m. Determine the normal force
acting on the car and the normal force acting on the driver. What is the
centripetal acceleration of the driver and the car? If the car is driven too fast, the
it can become airborne at the top of the hill. What is the maximum speed at
which the car travel over the hill without becoming airborne? Solution Visualize the
problem
Assume
the same radius for the motion of the car and driver are the same speed. Car
Driver
The
driver and car will have the same centripetal acceleration towards the centre
of curvature of the hill Travelling
too fast and becoming airborne
The
normal force becomes zero as the car leaves the ground.
Note:
Using unit vector notation makes it easier to keep track of the directions
and magnitudes of vector quantities. Note:
If you travel over a bump too fast, the car will become airborne. It does not
matter how good a driver you are, when the car leaves the ground you have no
control of the cars movement this has resulted in many fatal accidents.
|
|
Ian Cooper School of Physics University of Sydney If you have any feedback, comments,
suggestions or corrections please email Ian Cooper ian.cooper@sydney.edu.au |