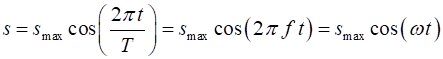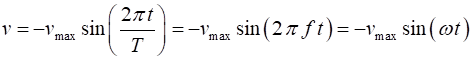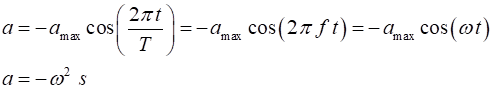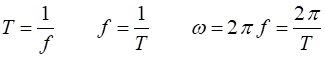VISUAL PHYSICS ONLINE

WAVES

SIMPLE HARMONIC MOTION

VIBRATIONS (OSCILLATIONS)

Anything that moves back and forth, to or fro, side to side, in-out-in, or up or down is said to be vibrating or oscillating.

Time variations that repeat themselves at regular intervals: periodic or cyclic behavior.

Fig. 1. Identify all the vibrations in the pictures.

A vibration is a periodic wiggle in time.

A wave is a periodic wiggle in both space and time.

The source of all waves is something that is vibrating.

Light and sound are both vibrations that propagate through space as a wave, but are two very different types of waves.

Sound is a mechanical wave that propagates through space as the vibrations of a material medium - solid, liquid or gas. Sound cant travel though a vacuum - a medium must be present for the vibrations to exist.

Light (electromagnetic radiation) is the vibrations of electric and magnetic fields. It is self-propagating and no medium is required, hence, it can travel through a vacuum.

A wave is a mechanism for the transfer of energy from one place to another without any material being transferred. Vibrations act a source of waves that travel outward from the source. It is the disturbance that propagates and not the medium.

VIBRATIONS (OSCILLATIONS)

When an object is disturbed from its equilibrium position, a restoring force acts on it to restore it back to the equilibrium position. If the object over shoots the equilibrium position and oscillates to and fro, the object is said to be vibrating. For example, if you suspend a stone from a piece of string (simple pendulum), the stone will vibrate back and forth when disturbed. When the stone is attached to the end of a spring and held vertically, the stone will bounce up and down when disturbed. Pendulums swing to and fro with such regularity, they were used for a long time to control the motion of most clocks.

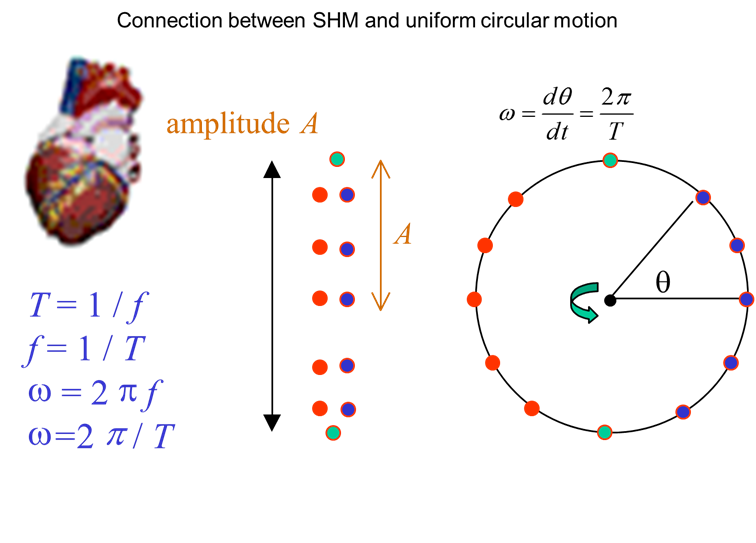
SIMPLE HARMONIC MOTION (SHM)

To model vibrations, we need to setup a simple model using approximations and simplifications. The simplest model to describe vibrations is called simple harmonic motion. 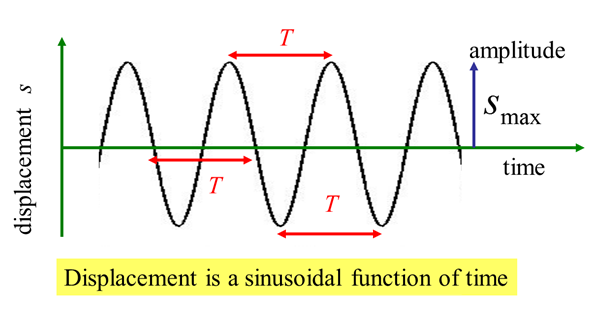In this model, the object will move backward and forward in a straight line about an equilibrium position with a period which is independent of the magnitude of the disturbance and the displacement of the object from its equilibrium position can be described by a sinusoidal function. For the vertical oscillations of an object, the frame of reference has the +Y axis pointing upwards and the equilibrium position corresponds to the Origin. The position of the object at any time t is given by the displacement .

Displacement

Velocity

Acceleration

Displacement amplitude is the maximum extent of a vibration or oscillation, measured from the position of equilibrium.

Velocity amplitude is the maximum speed of the oscillating object.

Acceleration amplitude is the maximum acceleration of the oscillating object.

The amplitude is always a positive number. The symbol is often used for the amplitude.

For SHM the acceleration is proportional to the displacement and it direction is opposite to the displacement.

Period is the time for one cycle of motion [s].

Frequency is the number of cycles in one second [hertz Hz 1 Hz = 1 s^-1]

1 kHz = 10³ Hz (kilo) 1 MHz = 10⁶ Hz (mega) 1GHz = 10⁹ Hz (giga)

Angular frequency [ rad.s^-1]

Phase angle [ rad ] angle must be measured in radians and time in seconds

The displacement , velocity and acceleration are all sinusoidal functions of time.

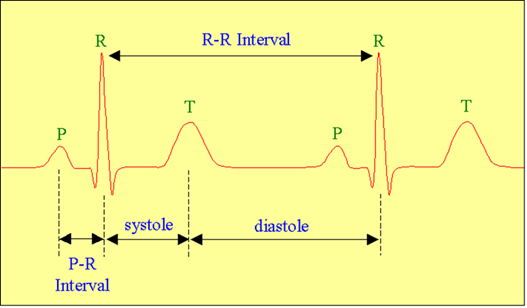
A periodic signal is the recording of an ECG.

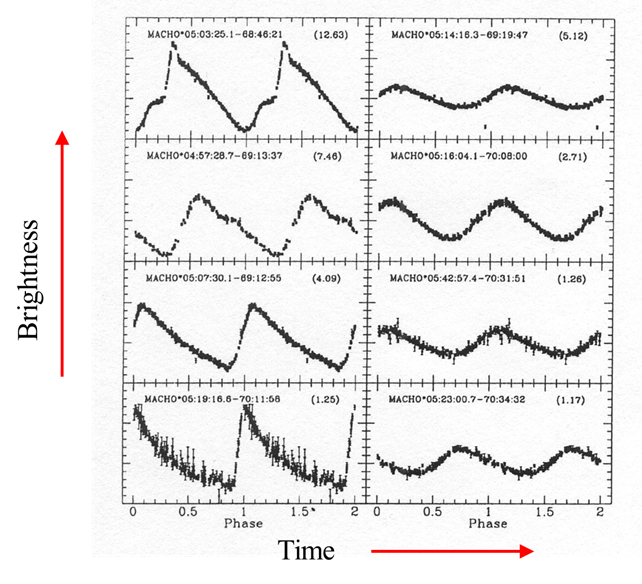
The brightness of stars varies periodically.

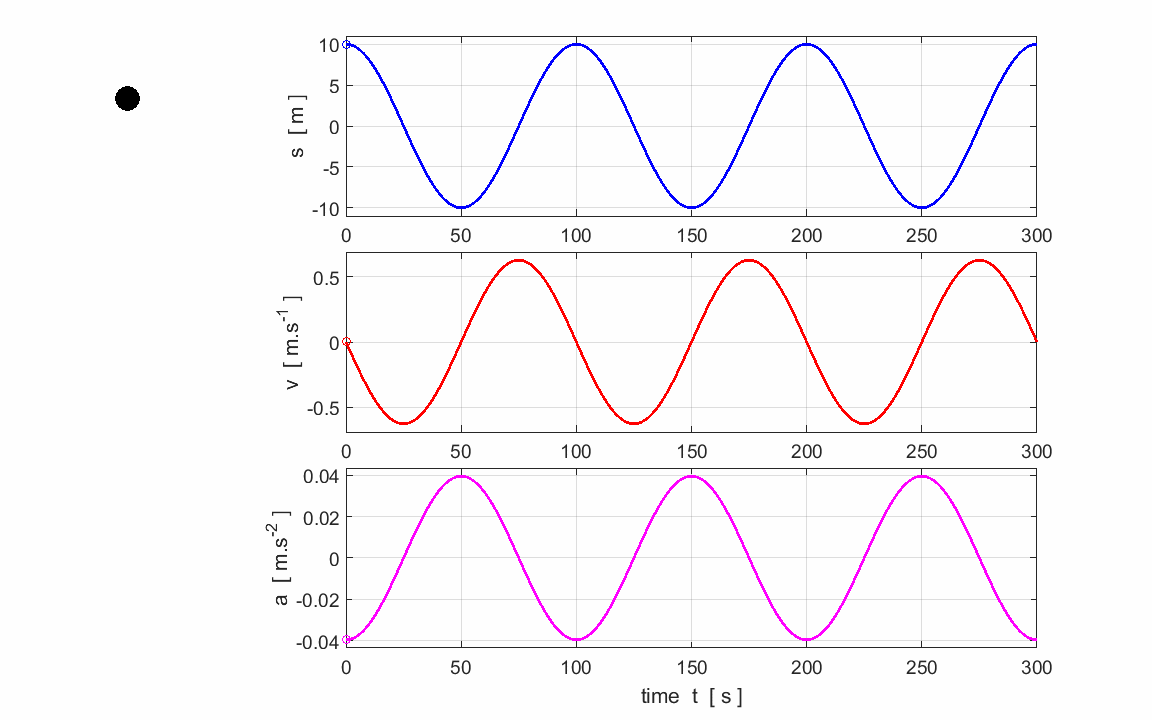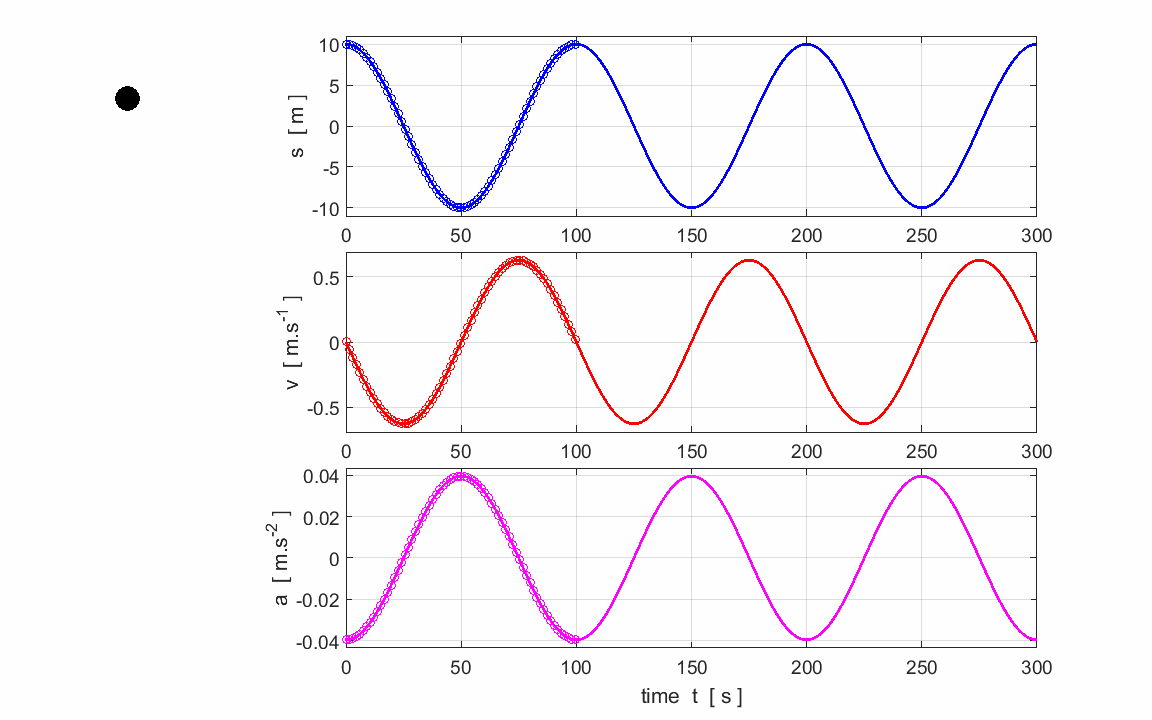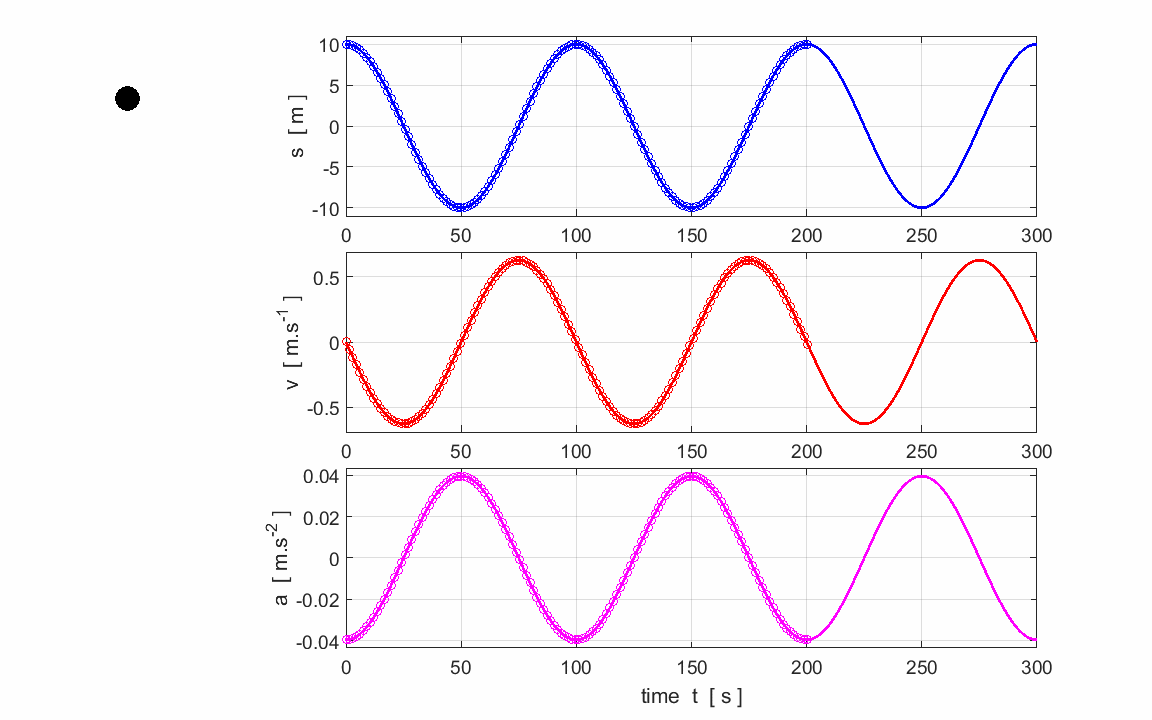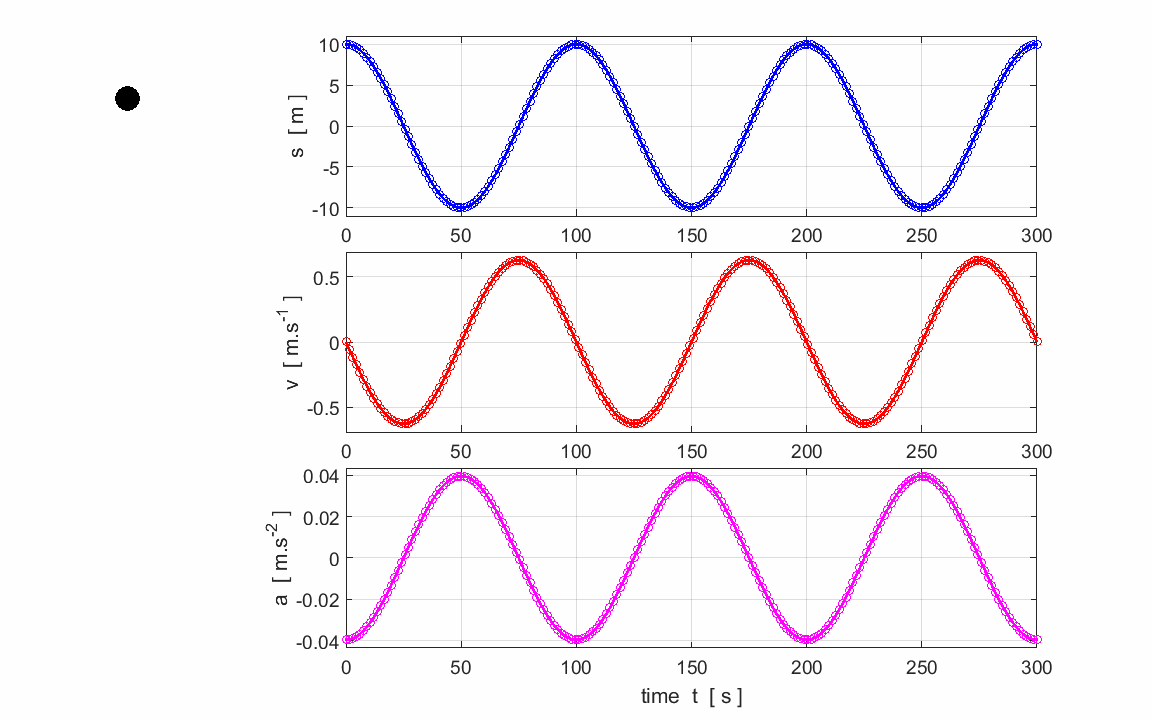
Fig. 2. An animation for an object executing SHM in the vertical direction.

Exercise 1

Watch the animation and check that the graphs do successfully describe the motion of the object.

Use the graphs to calculate and check your answers for the estimation of the following parameters:

Period, frequency and angular frequency

Amplitudes: displacement, velocity and acceleration

The slope of the tangent to a displacement vs time graph gives the velocity. Verify from the graphs.

The slope of the tangent to a velocity vs time graph gives the acceleration. Verify.

Predict the changes in the three graphs if

(1) The amplitude was decreased.

(2) The period was decreased.

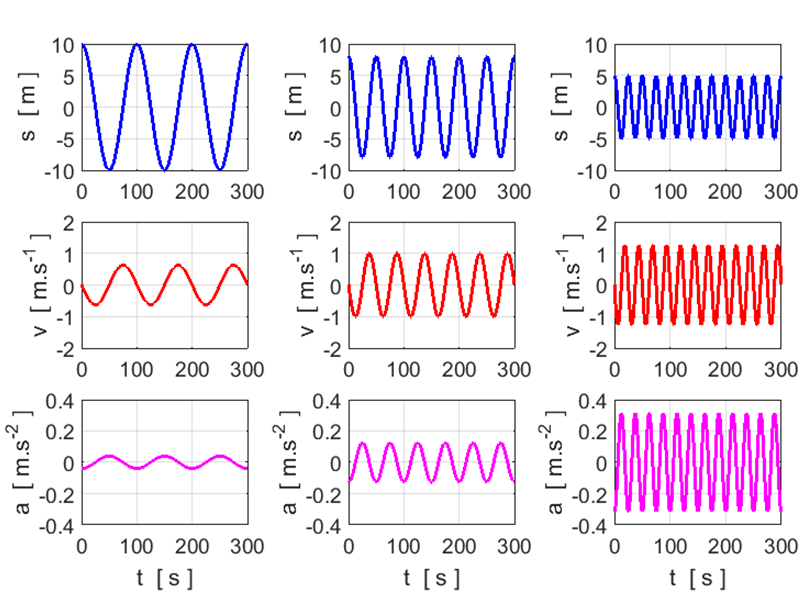
Exercise 2

Use the graphs to calculate and check your answers for the estimation of the following parameters:

Period, frequency and angular frequency

Amplitudes: displacement, velocity and acceleration

Doing Physics with Matlab

Download mscripts

Animation produced with osc_shm_01A.m

SHM graphs produced with osc_shm_01.m

VISUAL PHYSICS ONLINE

If you have any feedback, comments, suggestions or corrections please email:

Ian Cooper School of Physics University of Sydney

ian.cooper@sydney.edu.au