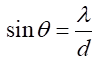VISUAL PHYSICS ONLINE WAVES SINGLE SLIT DIFFRACTION

Diffraction from single apertures

We know that when a wave passes through an opening, the waves spread in all directions diffraction. However, if we think about Huygens Principle, each point in the opening acts like a source of secondary waves which emit waves that spread out beyond the aperture. So, at certain points, these secondary waves may be in phase and interfere constructively, while at other points the waves maybe out of phase and interfere destructively. Therefore, when a wave passes through an opening a diffraction pattern maybe produced with distinctive regions of reinforcement (constructive interference) and regions of cancellation (destructive interference).

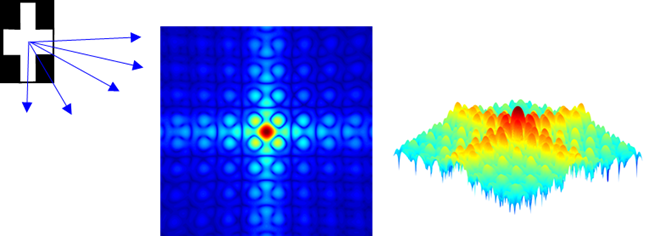
Fig. 1. Light passing through a cross-shaped aperture spreads and interferes to produce a diffraction pattern on a distance screen. The diffraction patterns shown correspond to the intensity of the light on the viewing screen using false colours. Regions of bright and dark are clearly seen in the plots.

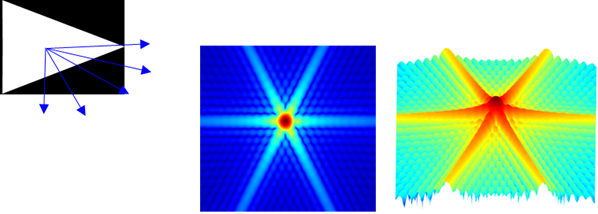
Fig. 2. Light passing through a triangular-shaped aperture spreads and interferes to produce a diffraction pattern on a distance screen. The diffraction patterns shown correspond to the intensity of the light on the viewing screen using false colours. Regions of bright and dark are clearly seen in the plots.

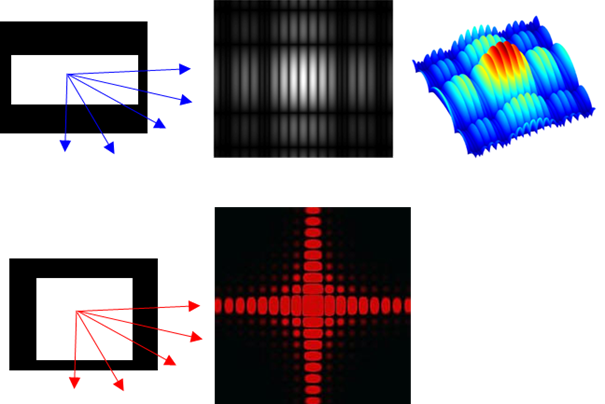
Fig. 3. Light passing through a rectangular-shaped aperture spreads and interferes to produce a diffraction pattern on a distance screen. The diffraction patterns shown correspond to the intensity of the light on the viewing screen using false colours. Regions of bright and dark are clearly seen in the plots.

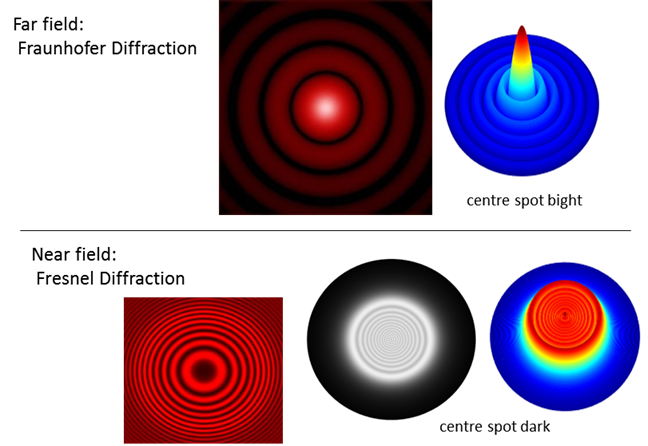
Fig. 4. Light passing through a circular aperture. If the viewing screen is a large distance from the aperture, we get a Fraunhofer diffraction pattern. If the viewing screen is near the aperture, the energy distribution becomes very irregular and unexpectantly, you can observe a dark spot at the centre of the image. This type of diffraction is called Fresnel diffraction.

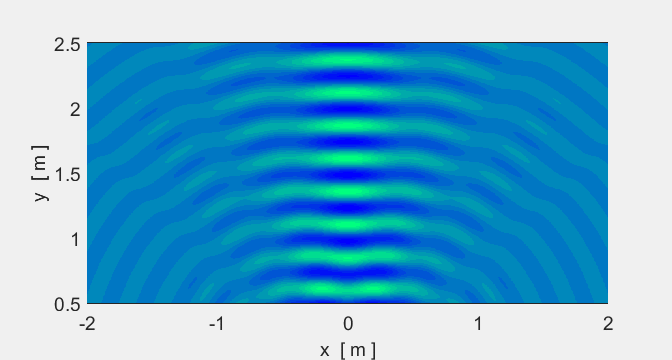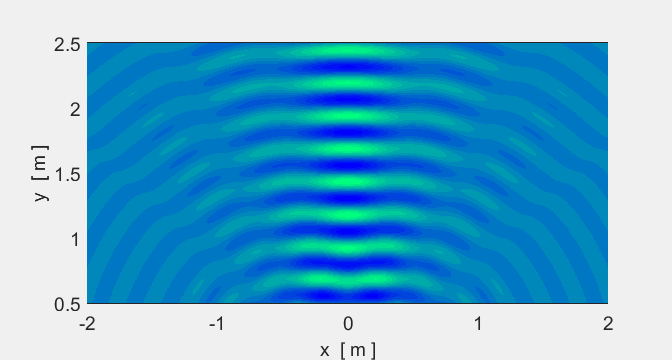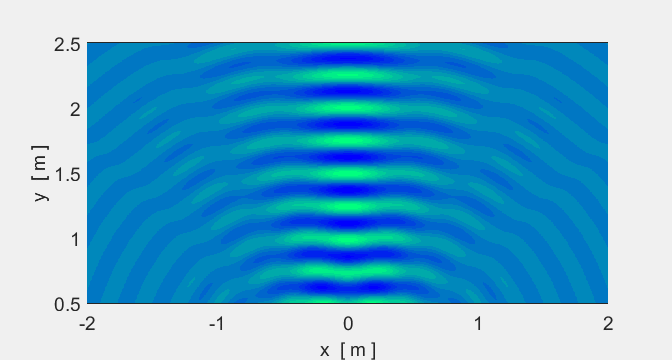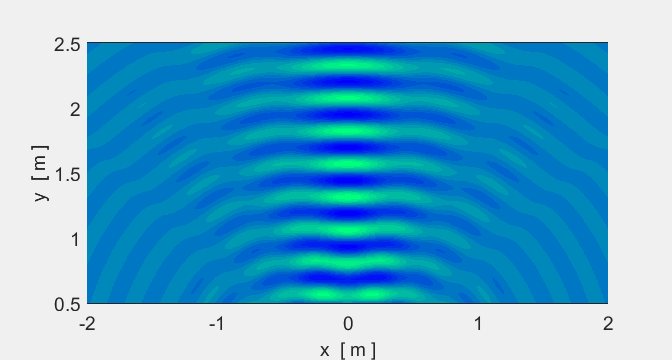
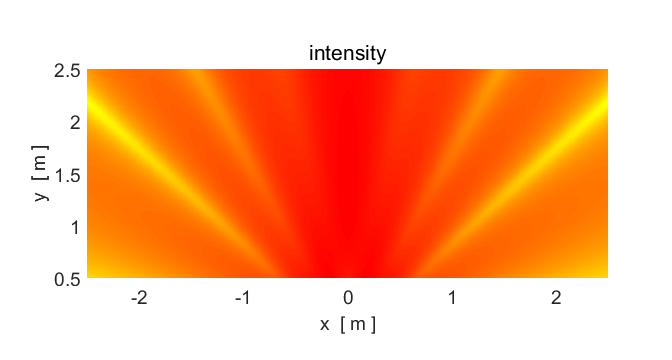
Diffraction from a single slit

Animation 1. Diffraction of water waves through an aperture of width (). As water waves pass through the aperture, they diffract (change direction). The waves from the opening also interfere with each other and give regions where there is destructive interference and the water would be calm. These regions are shown as the yellow nodal lines in the intensity graph (log scaling for the colour to better show regions of constructive interference (reinforcement red) and destructive interference (cancellation yellow).

Single slit diffraction with visible light

Consider monochromatic light of wavelength passing through a narrow slit of width d as shown in figure 9.

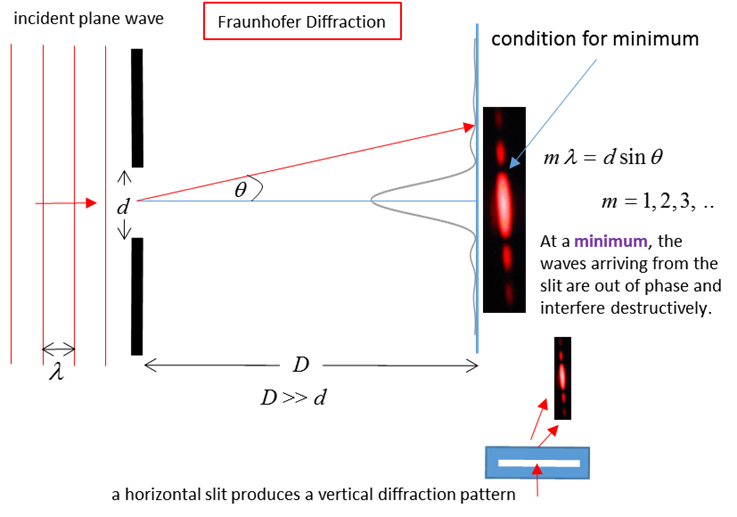
Fig. 6. Single-slit diffraction. When light of wavelength passes through the slit of width d, you observe a diffraction pattern of bright and dark fringes provided .

After passing the slit, the light is observed on a distant screen as shown in figures 6 and 7. When light passes through a slit, geometric optics predicts that this setup will produce a single band the same size as the slit. But, this is not what is observed, as shown in figures 6 and 7. According to Huygens Principle, each point within the slit can be considered as a source of new waves that radiate towards the screen. A Fraunhofer diffraction pattern is produced by the interference of these waves when . The Fraunhofer diffraction pattern is characterised by a very bright central maximum and a set of small bright secondary maxima (constructive interference). Each maxima is surrounding by dark fringes where the waves interfere destructively. The angular positions of the dark fringes is given by

xxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxx

The position of the first order dark fringe is

xxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxx

We know that the sine of angle cant be greater than 1 . Therefore, a diffraction pattern is only formed when . If the waves only spread after passing through the slit and there are no bright and dark fringes. If , the angular width of the diffraction pattern increases with larger wavelength and with decreasing slit width as shown in figures 10 and 11.

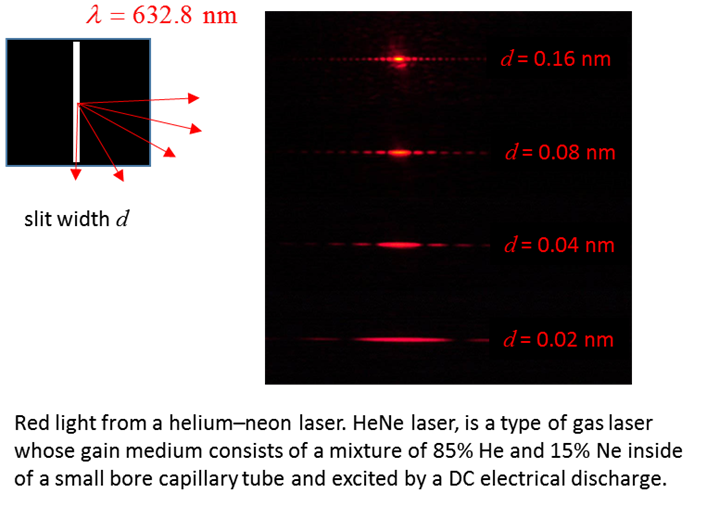
Fig. 7. Red light passing through a narrow slit. N.B. the smaller the width d of the slit the broader the diffraction pattern.

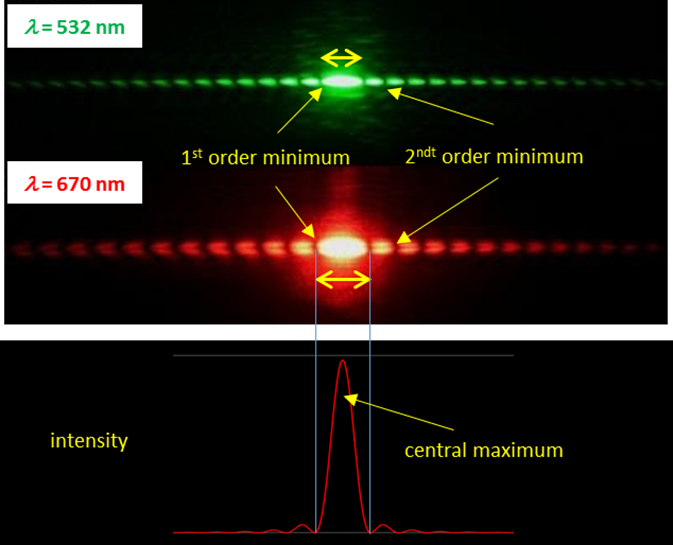
Fig. 8. Photographs of the diffraction for a single slit using green and red lasers. The diffraction pattern shows a strong central maximum (bright spot) surrounded by secondary maxima of much lower intensity. The dark fringes are identified by specify their order, m = 1, 2, 3,

N.B. the larger the wavelength, the wider the pattern.

VISUAL PHYSICS ONLINE

If you have any feedback, comments, suggestions or corrections please email:

Ian Cooper School of Physics University of Sydney

ian.cooper@sydney.edu.au