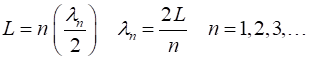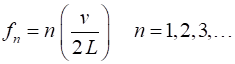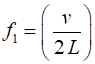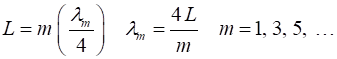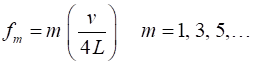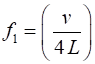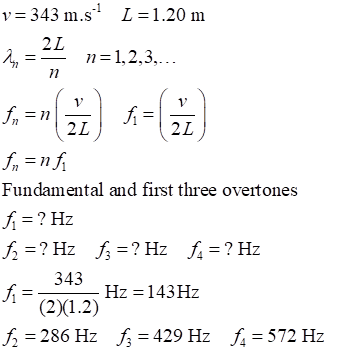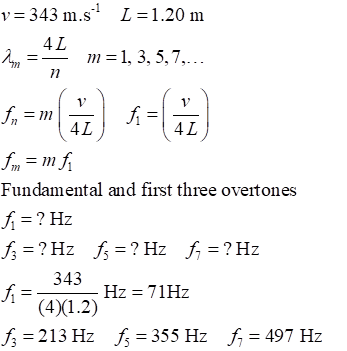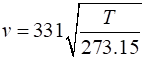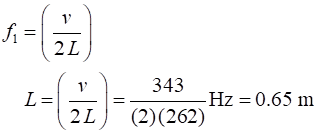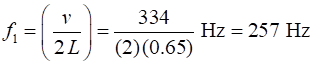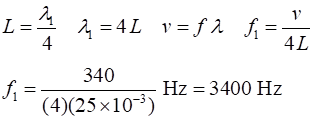|
|
WAVES MUSICAL INSTRUMENTS WIND
INSTRUMENTS |
Sound
Waves in Air
|
A sound
waves in air is an example of a longitudinal (compressional) wave the direction of the air particles vibrational
motion is in the same direction that the wave is propagating. The wave is characterised by a series of alternate compressions (condensations) and rarefactions (expansions)
as shown in figure 1 for a pure tone (single frequency) sound. The compressions
correspond to the crests and the rarefactions are the troughs of a wave. The propagation speed of sound in air
depends on the air temperature. At 20 oC,
the speed is v = 343 m.s-1.
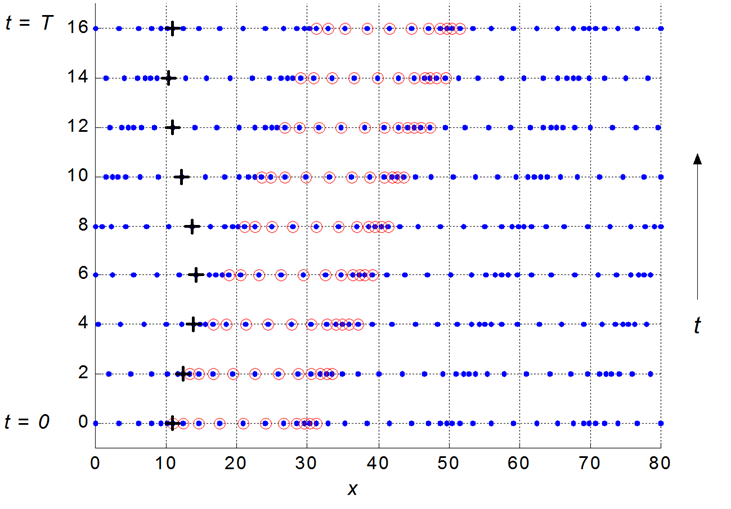
Fig.
1. Longitudinal wave for a pure tone:
Each particles displacement is a sinusoidal function of time as it is
executing simple harmonic motion as shown by the particle marked by the + sign. The wave advances 1
wavelength in a time interval of 1 period. The particles oscillate over very
small distances, whereas the wave itself propagates over much larger
distances. The wavelength is the distance between adjacent compressions or
between adjacent rarefactions. The compressions are represented by crests of
a wave and correspond to regions of an increase in pressure above atmospheric
pressure. A rarefaction corresponds to a trough and is an area of reduced
pressure below the atmospheric pressure. So, the pressure fluctuations above
and below atmospheric pressure also vary sinusoidal at the same frequency as
the displacement of the air particles.
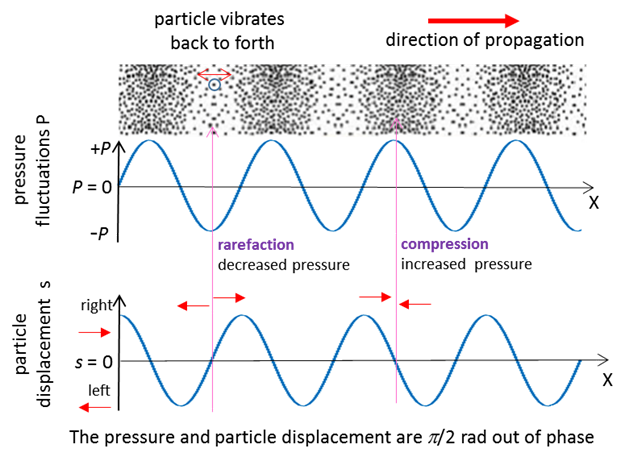
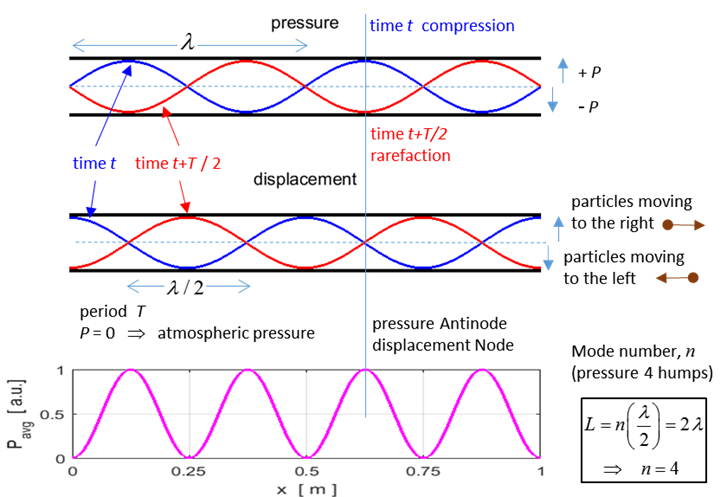
Fig.
2. Three ways to describe a sound
wave for a pure tone (single frequency) at one instant of time. (1) A plot
showing the individual displacements of the air molecules. (2) A graph of
pressure fluctuations versus position. Compression: particles pile up, so the
pressure is most positive. Rarefaction: particles pulled apart, so pressure
is most negative. When P = 0, the
actual pressure of the air is atmospheric pressure. (3) A graph of particle displacement as a
function of position. Where s >
0, particles are displaced to the right and where s < 0, particles are
displaced to the left. The pressure
and the particle displacement are cycle out of phase ( |
Standing waves and normal modes for vibrating air columns
|
The source of any sound is a
vibrating object. Almost any object can vibrate and hence become a source of
sound. Instruments such as woodwinds, the brasses and the organ pipes produce
sound from the vibrations of standing waves in a column of air with in a pipe
or tube. Standing waves can occur in any air cavity, but the relationships
between the natural frequencies of vibration are complicated except for long,
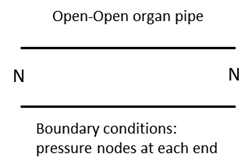
narrow tubes found in organ pipes. Most wind instruments are either
of the Open-Open
tube type or Open-Closed
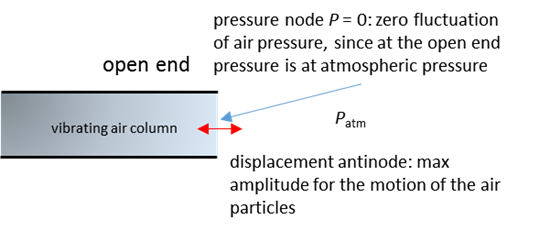
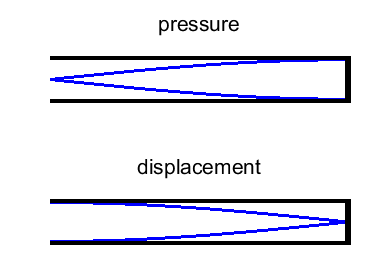
tube type. At an open end, the air in the tube comes into contact with the atmospheric air at atmospheric
pressure. Therefore, at an open end, there must be a pressure node, P = 0. The air particles at the open
end can vibrate freely and have maximum particle displacement. So, for the
particle displacement, the open end must correspond to a displacement
antinode.
Fig. 3. Boundary conditions at the open end of a
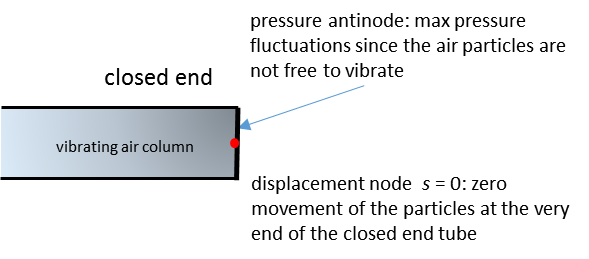
column of air in a tube. At a closed-end, the air in the
tube comes into contact the solid termination (instrument or mouth). The air
particles at the closed end cant vibrate freely and have zero particle
displacement, s = 0. Therefore, at
a closed end, there must be a displacement node. The air particles must accumulate at the
closed end because of zero displacement at the very end of the tube,
therefore, the pressure fluctuation at the closed end must correspond to a
pressure antinode.
Fig. 4. Boundary conditions at the closed end of a
column of air in a tube. When the air is
disturbed at one end of the wind instrument, the air vibrates with a variety
of frequencies, but only frequencies that correspond to the natural
frequencies of the standing waves will persist.
Note, the standing waves in the air column are due to reflections of
the waves at the ends of the air column. The waves propagating backward and
forward along the tube add as described by the superposition principle to
produce the standing waves at a discrete set of frequencies the natural
frequencies of vibration of the
air column.
Fig.
5. A dramatic example of standing
waves set up in a column of gas. Explain the pattern of the flames. Open-Open
tubes A stream of air is directed
against one edge of the opening or mouthpiece producing turbulent motion of
the air that sets up the vibrations of the air column. A flute is an example
of an Open-Open
tube. When the flautist plays a note, they do not entirely cover
the hole in the mouthpiece, but blow across the mouthpiece. The boundary
conditions are:
Pressure node at each end of the instrument
Displacement antinode at each end of the instrument
Fig. 5. A flute is an Open-Open tube. We can describe the vibrations
of the air inside a tube in terms of the displacement of the air particles or
the fluctuations in pressure above and below atmospheric pressure. Most
elementary physics texts discuss standing waves in terms of the particle
displacement. But, a much better approach is always to consider the pressure
fluctuations rather than displacements. When doing an experiment on standing
waves in air cavities a microphone is used which measures pressure, so, it is
better to explain the standing waves in cavities in terms of pressure. The air within a tube vibrates
in the form of a longitudinal wave standing wave. A normal mode of vibration
of a standing wave is often represented graphically as shown in figure 6 for
one of the natural frequencies. The representation of normal mode of standing
wave for a long, narrow pipe shown in figure 6, is a complex picture from
which you can extract much information you need to make sure you can
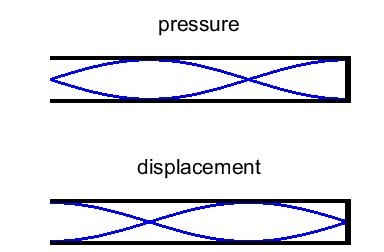
interpret such diagrams. The standing wave pattern for a tube open at both
ends can be shown in terms of the pressure variation or particle displacement
along the length of the tube. The diagram shows the fixed positions of the
nodes and antinodes. Note, a pressure node corresponds to a particle
displacement antinode, and vice versa. Adjacent nodes are separated by
Fig. 6. A normal mode of vibration for a long,
narrow tube with both ends open. For a long, narrow tube, there
must be pressure nodes at each end. To match these boundary conditions, only an integral multiples of half-wavelengths can fit into the
length L of the
tube for standing waves to form (1) Therefore, the natural
frequencies of vibration are (2) The integer n = 1 fundamental or
1st harmonic
n = 2 2nd
harmonic or 1st overtone n = 3 3rd
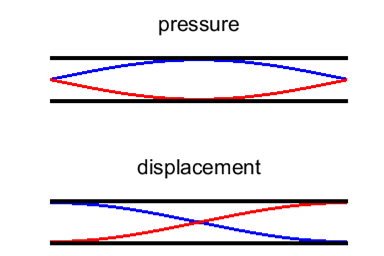
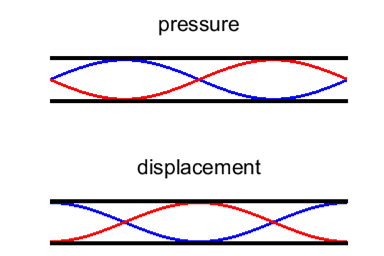
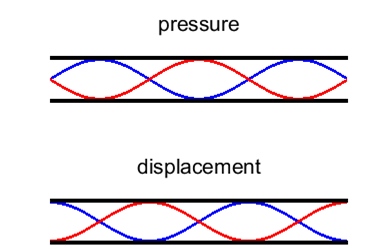
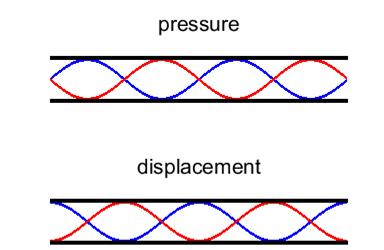
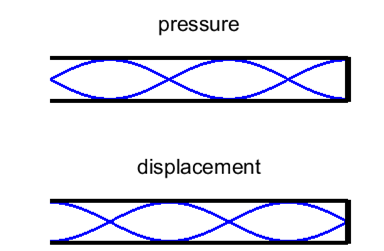
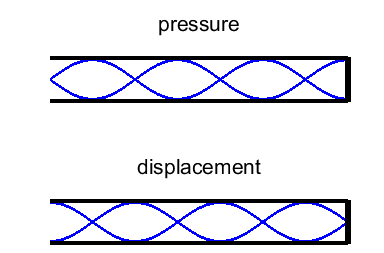
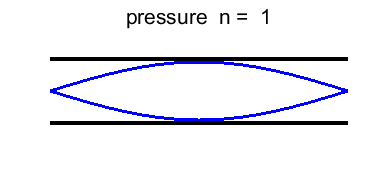
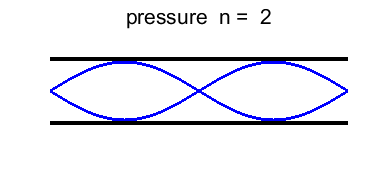
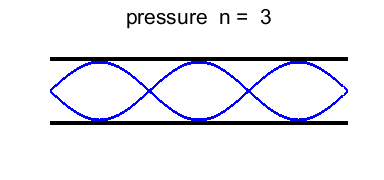
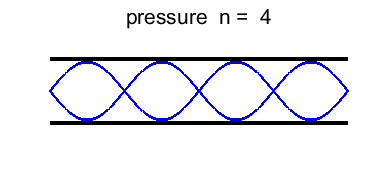
harmonic or 2nd overtone Figure 7 shows the standing wave pattern for the first six
harmonics. In the pressure distribution plots, the number of bumps
(antinodes) is equal to the normal mode number n. |
|
n
= 1 |
n
= 2 |
|
n
= 3 |
n
= 4 |
|
n
= 5 |
n
= 6 |
Fig. 7. Standing wave patterns for a long, narrow
tube open at both ends.
|
Open-Closed
tubes A clarinet is an example of a
wind musical instrument that is open at one end by the bell-shaped
termination and the other end is closed by the mouth.
Fig. 8. A clarinet is an Open-Closed tube type
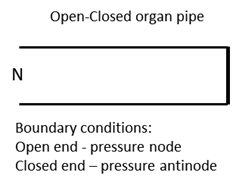
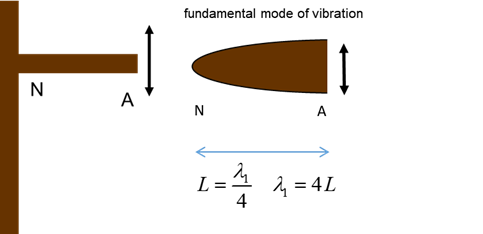
instrument. For a long, narrow tube, there
must be pressure node at the open end and a pressure antinode at the closed
end (particle displacement: antinode at open end and a node at the closed
end). To match these boundary conditions, only odd multiples of
quarter-wavelengths can fit into the length L of the tube for standing waves to form (3) Therefore, the natural
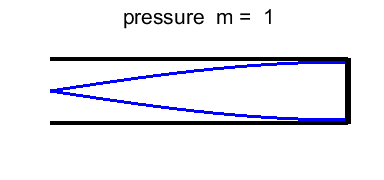
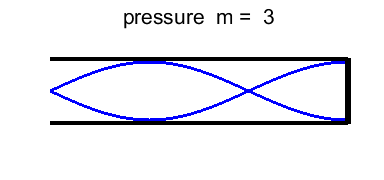
frequencies of vibration are (2) The odd integer m = 1 fundamental or
1st harmonic
m = 3 3rd
harmonic or 1st overtone m = 5 5th
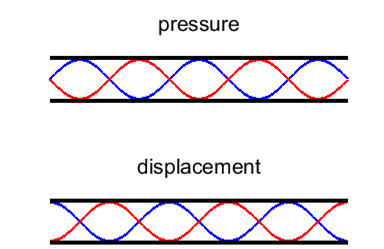
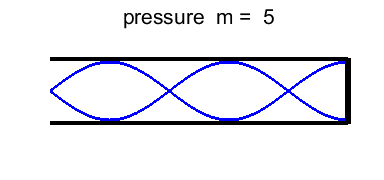
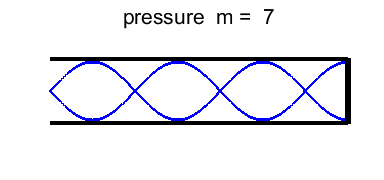
harmonic or 2nd overtone Figures 9 and 10 shows the standing wave pattern for normal
modes 1, 3, 5, 7 and 9. You can tell the normal mode number by counting the
number of quarter-wavelengths in the length of the tube. |
|
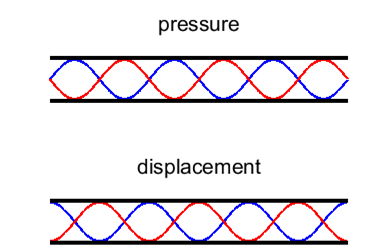
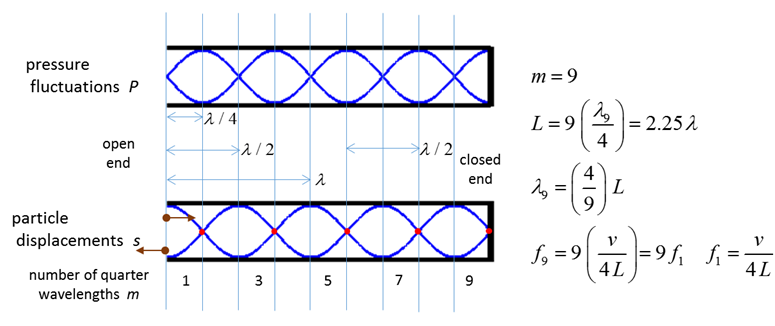
Fig. 9. Standing wave patterns for a long, narrow
tube that is open at one end and closed at the other end for the 9th
harmonic. |
|
m = 1 Fundamental 1st harmonic |
m = 3 3rd
harmonics 1st overtone |
|
m = 5 5th
harmonics 2nd overtone |
m = 7 7th
harmonics 3rd overtone |
|
Fig. 10. Standing wave patterns
for a tube that is an Open-Closed type. |
|
|
Organ pipes make use of both Open-Open and Open-Closed types of
tubes. Notes of different frequency are produced using different pipes with
different lengths ranging from ~ 10 mm to more than ~ 5 m. Different notes of
instruments like the flute and clarinet are obtained by shortening the length
of the tube by uncovering holes along its length. In a trumpet, pushing down
on the valves pens additional lengths of the tube. In all cases, the longer
the length of the vibrating air column, the lower the frequency of the
note. An Open-closed tube will sound a
lower note than an Open-Open tube of the same length. |
|
Example An narrow
organ pipe has a length of 1.20 m. The organ pipe is open at both ends. What is the natural frequency of
the fundamental and the first three overtones? One end of the pipe is then
closed. What are the new frequencies for the fundamental and the first three
overtones? Compare your two sets of frequencies. Draw the standing waves patterns
for the pressure distributions in the organ pipe for the open-open ends and for
the open-closed ends. (speed of sound in air v
= 343 m.s-1). Solution
Visualize the physical situation
Think about how you will approach the problem (Identify, Setup,
Execute, Evaluate)
Annotated scientific diagrams |
|
|
|
|
|
|
|
|
|
|
|
All the harmonics are present. |
Only the odd harmonics are
present and the fundamental frequency of the Open-Closed pipe is only the
value of the fundamental for the Open-Open pipe. |
|
|
Example A flute when all its holes are
covered is designed to have a fundamental frequency of 262 Hz (Middle C)
at a temperature of 20 oC. What is the
approximate length of the flute? What would be the fundamental frequency of
the flute when played at only 5.0 oC? Speed of sound in air Solution Assume that the flute is long
and narrow and that it can be modelled as a straight tube with Open-Open
ends. T = 20 oC = 293.15 K v = 343
m.s-1 f1 = 262 Hz L = ? m T = 5.0 oC = 278.5 K v = 334
m.s-1 L = 0.65
Hz f1 = ? Hz Why do performers take a long
time to tune their wind instruments? Note, the effect of temperature
on stringed instruments is much smaller. |
|
Woodwind instruments
are not necessarily made of wood e.g., saxophone, but they do require wind to
make a sound. They basically consist of a tube with a series of holes. Air is
blow into the top of the tube, either across a hole or past a flexible reed.
This makes the air inside the tube vibrate and give out a note. The pitch of
the note depends upon the length of the tube. A shorter tube produces a
higher note, and so holes are covered. Blowing harder makes a louder sound.
To produce deep notes woodwind instruments, have to
be quite long and therefore the tube is curved. Brass
instruments (usually made of brass) consist of a long pipe that is usually
coiled and has no holes. The player blows into a mouthpiece at one end of the
pipe, the vibration of the lips setting the air column vibrating throughout
the pipe. The trombone has a section of pipe called a slide that can be moved
in and out. To produce a lower note the slide is moved out. The trumpet has
three pistons that are pushed down to open extra sections of tubing. Up to
six different notes are obtained by using combinations of the three
pistons.
|
|
Example A narrow glass tube 0.500 m long
and sealed at its bottom end is held vertically just below a loudspeaker that
is connected to an audio oscillator and amplifier. A tone with a gradually
increasing frequency is fed into the tube, and a loud resonance is first
observed at 170 Hz. What is the speed of sound in the room? [ Answer 340 m.s-1 ]
|
|
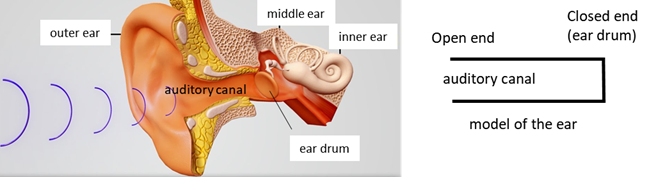
Example What are the natural frequencies
of vibration of a human ear? Why do sounds ~ (3000 4000) Hz
appear loudest? Solution
Assume the ear acts as pipe open
at the atmosphere and closed at the eardrum. The length of the auditory canal
is about 25 mm. Take the speed of sound in air
as 340 m.s-1. L = 25 mm = 25x10-3 m v = 340 m.s-1 For an air column closed at one
end and open at the other: Fundamental frequency f1 = ?
Hz If the ear is excited at a
natural frequency of vibration, then large amplitude oscillations can be
excited (resonance). Hence, sounds will appear loudest in the frequency range
from about 3000 Hz to about 4000 Hz. |
|
Example Wind can be noisy a tree can
howl and a chimney can moan. Why is this so? What is causing the noise? Solution Jets
of air in the wind cause vibrations which produce sound. Why does a tree
howl? Consider a branch of a tree. It acts a rod
with a displacement node at the end attached to the truck of the tree and an
antinode at the other end.
The
standing wave pattern for the branch is such that Why does the
chimney moan?
|
|
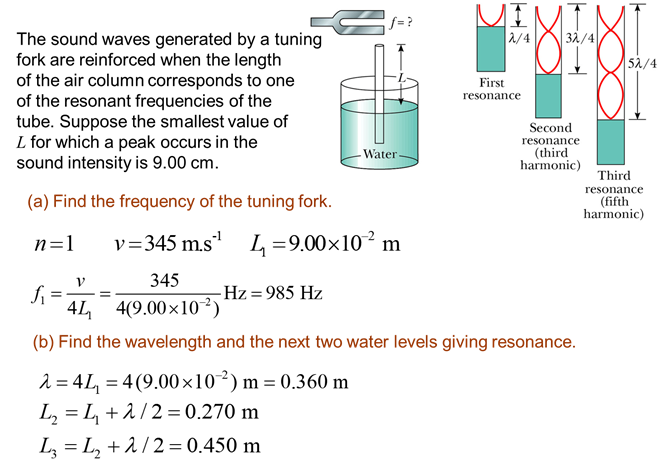
Example Resonance
|
|
If you have any feedback, comments, suggestions or corrections
please email: Ian Cooper School of
Physics University of Sydney ian.cooper@sydney.edu.au |