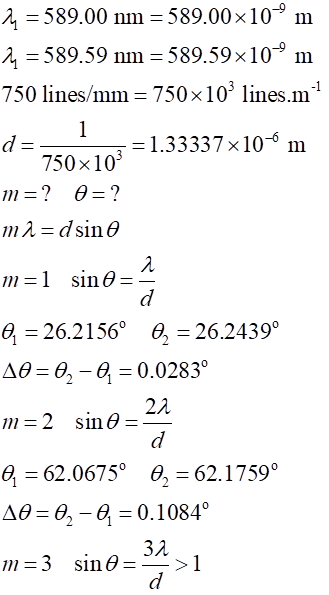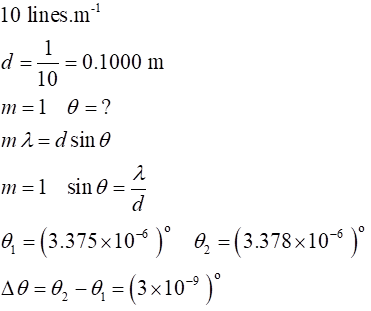|
|
WAVES INTERFERENCE DIFFRACTION GRATING |
|
When there is a need to separate light of different wavelengths
with high resolution, then a diffraction grating
is most often the tool of choice. Diffraction gratings are widely used
in application for measuring atomic spectra in both laboratory instruments
and telescopes. A large number of parallel, closely
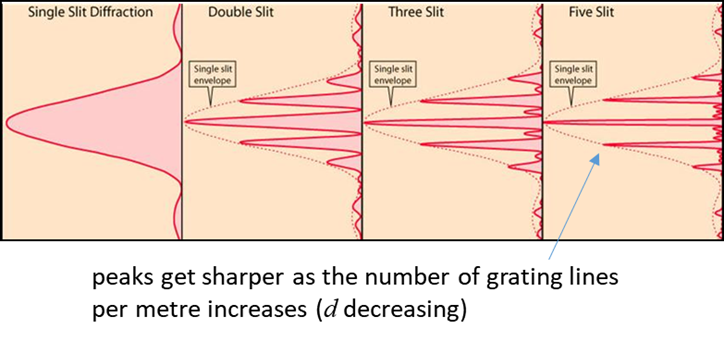
spaced slits constitutes a diffraction grating. The condition for maximum
intensity is the same as that for the double slit or multiple slits, but with
a large number of slits the intensity maximum is
very sharp and narrow, providing the high resolution for spectroscopic
applications. The peak intensities are also much higher for the grating than
for the double slit.
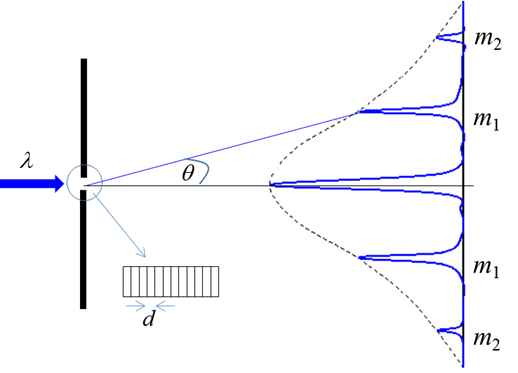
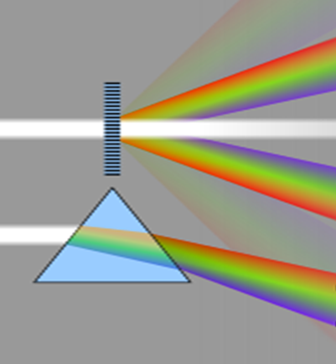
The diagram above illustrates the effect of a grating on a
monochromatic source of light. The central maximum is also called the zero order maximum. The position of higher order maximum
is given by the equation
where m = 1, 2, 3, is the order number of
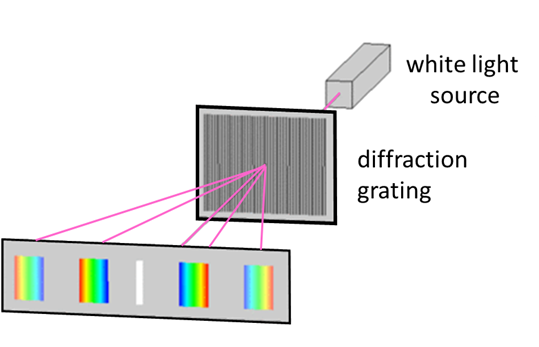
the bright bands, When white light passes through a diffraction grating, the light
of different wavelengths emerge at different angles.
As the number of grating lines per metre increase (d smaller) the maxima become narrower.
So, for gratings with a large numbers of lines per
metre will have peaks are very sharp and one can make very accurate
wavelength measurements. The resolution is also very good because two wavelengths
that close together, will be displayed as two distinguishable peaks.
Gratings have a much better resolution in resolving wavelengths that
prisms.
The surface of a CD acts like a diffraction grating
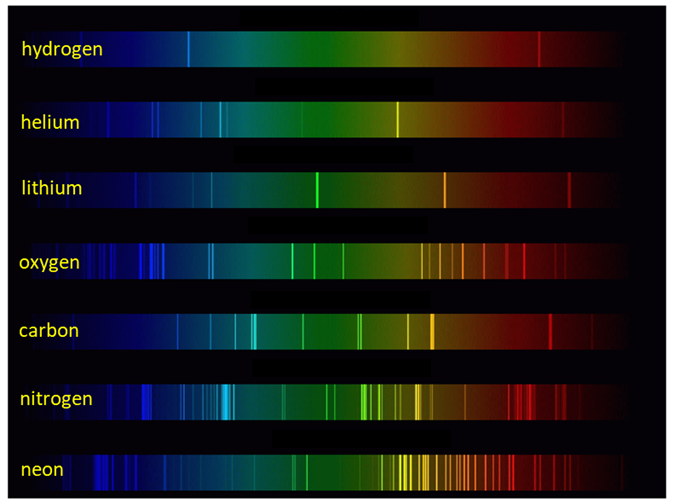
Using diffraction gratings to identify elements
|
|
Example Yellow sodium light which consists of two wavelengths 589.00 nm
and 589.59 nm falls on a grating with 750 lines / mm. Determine diffraction
angles and allowed diffraction orders. What are the diffraction angles for the order number m = 1, if the grating only had 10 lines / m? Solution
The difference in the angles for the two wavelengths is easily
measured The maximum order is m
= 2 For the grating with only 10 lines/m gives very small diffraction
angles and the two lines would not be resolved. The larger the number of
lines/m, the smaller the separation distance d between the lines and the
better the resolution.
|
|
If you have any feedback, comments, suggestions or corrections
please email: Ian Cooper School of
Physics University of Sydney ian.cooper@sydney.edu.au Ian Cooper |