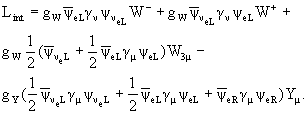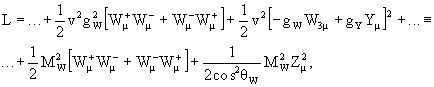W и Y можно ввести как калибровочные поля, что
обеспечивает перенормируемость теории электрослабых взаимодействий. Мы уже
познакомились с методом построения лагранжианов, инвариантных относительно
локальных калибровочных преобразований, на примере электромагнитного поля,
изотриплета полей векторных ρ-мезонов и
октета глюонов. В теории фотона как калибровочного поля мы имели дело с
преобразованием по группе U(1), в теории ρ-мезонов
как калибровочных полей у нас были преобразования по группе изоспина SU(2). Мы
уже ввели понятие слабого изоспина, а теперь потребуем локальной калибровочной
инвариантности лагранжиана левоспиральных лептонных ( и кварковых ) полей
относительно преобразований в слабом изотопическом пространстве по группе SU(2)L,
а также лагранжиана левоспиральных и правоспиральных полей по группе U(1). В
целом мы строим лагранжиан, инвариантный относительно локальных калибровочных
преобразований по группе SU(2)L ×
U(1). При этом мы, рассматривая отдельно лево- и правоспиральные компоненты
лептонов, вынуждены положить их массы равными нулю. Действительно, массовый член
спинорного поля ψ(x) в лагранжиане билинеен
по полю и следующим образом запишется через лево- и право-спиральные
компоненты спинорного поля ![]()
![]()
Легко видеть, что он оказывается неинвариантным относительно калибровочных
преобразований, не обладающих право-левой симетрией.
Нам надо получить выражение для трех поколений
лептонов. Но, как понятно, достаточно написать выражение для одного
левоспирального слабого изодублета ![]()
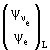
лептонов ![]() и соответствующего правоспирального слабого изосинглета eR:
и соответствующего правоспирального слабого изосинглета eR:
![]()
Этот лагранжиан инвариантен относительно глобального калибровочного преобразования
![]()
![]()
где матрицы Паули ![]() действуют в слабом изотопическом пространстве, а
действуют в слабом изотопическом пространстве, а ![]() - произвольные
вещественные фазы.
- произвольные
вещественные фазы.
Потребуем теперь инвариантности лагранжиана относительно
локальных калибровочных преобразований, когда ![]() и
и ![]() являются функциями x. Но, как и в предыдущих случаях, первоначальный лагранжиан
L0 неинвариантен относительно подобных локальных калибровочных
преобразований:
являются функциями x. Но, как и в предыдущих случаях, первоначальный лагранжиан
L0 неинвариантен относительно подобных локальных калибровочных
преобразований:
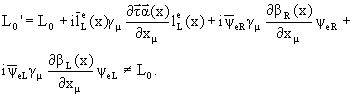
Для того, чтобы убрать члены, нарушающие калибровочную инвариантность, введем
слабый изотриплет векторных полей ![]() и слабый изосинглет
и слабый изосинглет ![]() с калибровочными преобразованиями
с калибровочными преобразованиями
![]()
где U = ![]() ;
;
![]()
Взаимодействие этих полей с лептонами ![]() e
e
|
(19) |
Итак, требование инвариантности лагранжиана
свободных лептонных полей относительно локальных калибровочных преобразований по
группе SU(2)L x SU(1) приводит к появлению четырех безмассовых
векторных полей ![]() , Y,
взаимодействующих с этими лептонными полями. Ранее уже было показано, как поля с
нулевым электрическим зарядом W3
, Y,
взаимодействующих с этими лептонными полями. Ранее уже было показано, как поля с
нулевым электрическим зарядом W3
Это преобразование практически завершает построение единой
калибровочной теории слабых и электромагнитных взаимодействий, именуемой теорией
электрослабых взаимодействий.
Мы рассмотрели сектор лептонов ![]() e
e
Остается разрешить еще одну проблему, что, однако,
оказывается невозможным без выхода за рамки рассмотренной калибровочной модели.
Это проблема масс квантов слабого поля W±, Z, которые в
полученных формулах равны нулю. Напомним, что экспериментально MW ![]() 80 ГэВ, а MZ
80 ГэВ, а MZ![]() 90 ГэВ.
90 ГэВ.
Для решения проблемы ненулевых масс слабых векторных бозонов
Хиггсом был предложен механизм так называемого спонтанного нарушения симметрии,
который устроен таким образом, что в результате поля W±,
Z оказываются массивными, а электромагнитное поле
Скалярные поля и калибровочные бозоны
Нам придется рассмотреть формальное построение
калибровочных полей не над спинорными полями, а над скалярными. Пусть задано
скалярное заряженное поле φ(x),
удовлетворяющее уравнению Клейна-Гордона ![]() , каковое может быть получено из
лагранжиана:
, каковое может быть получено из
лагранжиана:
![]()
Введем локальное калибровочное преобразование
![]()
Начальный лагранжиан L0 неинвариантен, как и следовало ожидать, относительно этого преобразования:
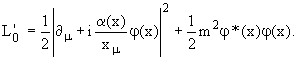
Введем безмассовое векторное поле ![]() со знакомым
калибровочным преобразованием:
со знакомым
калибровочным преобразованием:
![]()
Тогда лагранжиан, в который мы введем еще самодействие поля
φ(x) через член λ|φ(x)|4
и свободное поле ![]()
![]() ,
где
,
где ![]() ,
,
![]()
оказывается инвариантен относительно локального калибровочного
преобразования.
Остается попытаться ввести массу калибровочного бозона, для
чего мы и ввели самодействие. Будем рассуждать следующим образом. Потрактуем два
последних члена в L в качестве некоторого потенциала V(φ)
как функции переменной φ. Этот потенциал
имеет минимум в точке φ= 0 при m2 > 0,
λ > 0. А что произойдет при m2 < 0,
λ < 0? Минимум сместится из φ = 0 в
φ = (|m2|/2λ)1/2.
Вакуум оказывается вырожденным, а соответствующее вакуумное среднее отлично от
нуля, <φ>0 = v![]() 0! Формально
введем новое поле χ = φ(х) - v так , чтобы
новое поле имело обычный невырожденный вакуум, <χ>0 = 0,
и перепишем L, заменив поле φ на поле
χ, этим самым спонтанным образом нарушив
калибровочную инвариантность построенного лагранжиана:
0! Формально
введем новое поле χ = φ(х) - v так , чтобы
новое поле имело обычный невырожденный вакуум, <χ>0 = 0,
и перепишем L, заменив поле φ на поле
χ, этим самым спонтанным образом нарушив
калибровочную инвариантность построенного лагранжиана:
![]()
Подробно распишем первый член, который только и важен для понимания механизма генерации массы калибровочного бозона:
![]()
Последний член естественно трактовать как массовый член калибровочного поля ![]() .
.
Это и есть решение проблемы генерации массы
калибровочных бозонов.
Мы здесь вынужденно опустили некоторые вопросы,
например, связанные с голдстоуновскими частицами, постаравшись возможно более
просто изложить суть дела.
А теперь рассмотрим задачу введения масс
калибровочных бозонов W±, Z. Поскольку они обладают
слабым изоспином, следует ввести уже не одно, а несколько вспомогательных
скалярных полей.
Пусть заданы дублет скалярных заряженных
полей φ(x), и, соответственно, ему
сопряженный дублет ![]() :
:
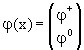 ,
, ![]()
Эти поля описываются лагранжианом того же вида
![]()
только здесь поля φ(x) - слабые изодублеты. Введем локальное калибровочное преобразование относительно группы SU(2) × U(1):
![]()
Начальный лагранжиан L0 неинвариантен, как и следовало ожидать,
относительно этого преобразования. "Удлиним" производную, введя калибровочные
поля ![]() ,
,![]() таким образом,
чтобы искомый лагранжиан оказался инвариантным относительно заданных
калибровочных преобразований:
таким образом,
чтобы искомый лагранжиан оказался инвариантным относительно заданных
калибровочных преобразований:
![]()
Переходя к полю χ = φ - v с нулевым ваккумным средним и раскрывая скобки в первом члене, получаем (удержим только интересующие нас вклады и обратим внимание на нейтральную комбинацию
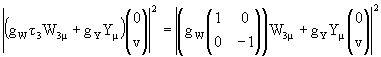 ):
):
|
(20) |
где мы воспользовались одним из обратных к (18) соотношений:
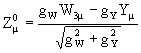
тогда как второе соотношение
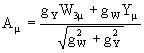
по построению отсутствует в лагранжиане. Иными словами, мы сообщили массу
заряженным W±- бозонам и нейтральному
Z -бозону, а фотон, как и должно, остался при нулевой массе. Отметим, что массы
W±-
бозонов и Z -бозона оказываются связанными друг с другом через угол Вайнберга: MW/MZ
= cos![]() W.
Этот результат находится в прекрасном согласии с экспериментом. Действительно,
MW = 80.419+0.056 ГэВ, MZ = 91.1882+0.0022 ГэВ,
а cos2θ
W.
Этот результат находится в прекрасном согласии с экспериментом. Действительно,
MW = 80.419+0.056 ГэВ, MZ = 91.1882+0.0022 ГэВ,
а cos2θ
Подобным образом можно ввести массы лептонов и кварков.
Достаточно ввести взаимодействие скалярных частиц с фермионами. Рассмотрим это
на примере электрона. Как мы уже знаем, левоспиральная часть электрона
входит в слабый изодублет с электронным нейтрино, а правоспиральная часть
является слабым изосинглетом. Лагранжиан должен быть скаляром по слабому
изоспину. Естественно для этого свернуть лептонный и скалярный изодублеты:
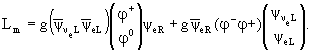
Этот лагранжиан калибровочно инвариантен, так как калибровочные преобразования над фермионными изодублетом и изосинглетом в точности компенсируются по построению калибровочными преобразованиями над дублетом хиггсовских бозонов. Стандартным приемом переходя к полю χ = φ - v с нулевым ваккумным средним, получаем эффективную массу электрона:
![]()
Таким же образом можно сделать массивными остальные лептоны и кварки. Обратим внимание, что при этом возникают многочисленные вершины, соответствующие взаимодействию фермионов с хиггсовскими полями. Пока эти вершины, если они даже реальны, остаются вне досягаемости эксперимента.