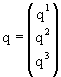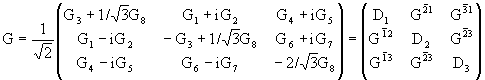В цветном пространстве разделение
кварков по цветам также условно. С одной стороны,
всегда можно условиться, какой именно кварк
несет определенный цвет во всем
пространстве-времени. Этого можно добиться
посредством глобального калибровочного
преобразования в пространстве цвета. С другой
стороны, концепция локализованного поля, лежащая
в основе обычных физических теорий, как мы уже
видели на примерах, естественно ведет к
требованию инвариантности теории относительно
локальных калибровочных преобразований в
цветном пространстве.
Подобно рассмотренным случаям с
электроном и нуклоном, напишем лагранжиан для
свободных полей трехцветных кварков qa , a = 1,
2, 3 . Точнее, кварк определенного аромата q есть
3-спинор группы SU(3)C в цветном пространстве:
|
(12) |
аналогично тому, как нуклон является 2-спинором
группы SU(2) в изопространстве. И подобно тому, как
протон переводился в нейтрон с помощью 2-мерной
матрицы 
-,
кварк цвета 1 переводится в кварк цвета 2 или 3, но
уже с помощью 3-мерной матрицы.
Лагранжиан, описывающий свободное
движение цветных кварков определенного аромата
в пространстве-времени, имеет вид, аналогичный (7):
где q(x) - дираковский спинор, который является
еще 3-спинором в цветном пространстве (см. (12)).
Этот лагранжиан инвариантен относительно
глобального калибровочного преобразования в
цветном пространстве, задаваемого 3
× 3-унитарной
матрицей, которую удобно записать в виде
экспоненты от линейной комбинации 8 линейно
независимых 3 × 3-эрмитовых матриц 
k,
q'(x) = Uq(x),
Здесь 
k,k,
i, j,
k = 1, ..., 8. ( fkij-так наз. структурные
константы SU(3), отличные от нуля значения которых
есть f123=1, f147= f246 = f257 = f345
= 1/2, f156 = f367= - 1/2, f458 = f678 = 
.) Потребуем
теперь в духе наших предыдущих рассуждений
инвариантности искомого лагранжиана
относительно локального калибровочного
преобразования, когда k являются функцией x:
q'(x) = U(x)q(x), |
(13) |
Но, как и в предыдущих двух случаях для электрона и нуклона, L0C неинвариантен относительно локального калибровочного преобразования (13):
Для того, чтобы убрать члены, нарушающие
калибровочную инвариантность, необходимо ввести
уже 8 безмассовых векторных полей 
k = 1,...8 с калибровочным
преобразованием
Взаимодействие этого поля с кварками зададим лагранжианом
которому соответствует фейнмановская диаграмма
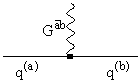
Рис.10
где 
= 1, 2, 3 нумерует столбцы,
а b = 1, 2, 3 строки матриц k.
|
(14) |
где
.
Каждый глюон несет цвет и антицвет, причем
диагональные комбинации ни в коем случае не
бесцветны! Кварк цвета a излучает глюон цвета a и
антицвета b, переходя в кварк цвета b. Скалярная по
цвету (бесцветная) комбинация 
в обмене между кварками
не участвует.
Запишем окончательное выражение
для лагранжиана, инвариантного относительно
локальных калибровочных преобразований
неабелевой группы SU(3)C в пространстве
цвета:
|
(15) |
где 
, k = 1, 2,
...8, - тензор свободного глюонного поля,
преобразующийся при локальных калибровочных преобразованиях как
Так же, как и в теории Янга-Миллса, из-за нелинейности по полю тензора глюонного поля возникают 3- и 4- глюонные вершины:
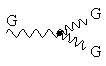
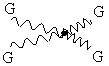
Рис.11
Эти выражения в сущности составляют основу квантовой хромодинамики.
Упражнения
- Построить 3 x 3 матрицы, переводящие кварк цвета 1 в кварки цветов 2 и 3 (воспользоваться равенством (14) и аналогией с соотношениями для нуклона (6) ).
- Показать, что лагранжиан (15) инвариантен относительно локальных калибровочных преобразований (13).
