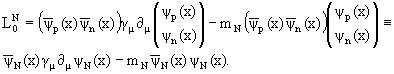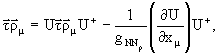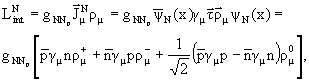©hoo$e ЛAнg?Age©///?Ang?Age® Ekohomei©A TALKiNg ?.?.м.?.

geo.rf.gd

   

4. Ро-мезон как калибровочное поле

    Следующим примером уже неабелевой теории калибровочных полей является теория Янга Миллса. В 1954 году Янг и Миллс решили попробовать построить теорию сильных взаимодействий, исходя из локальных калибровочных преобразований в изотопическом пространстве. Векторные ρ-мезоны были в эти годы только открыты, и представлялось, что они, наряду с пионами, могут оказаться искомыми квантами сильного поля.
    Сейчас такой подход к описанию сильных взаимодействий представляет только академический интерес. Однако, исходная идея достаточно проста и позволяет понять общий путь построения произвольных неабелевых калибровочных теорий.
    Что же представляет собой "изотопическое пространство"? Поскольку протон и нейтрон обладают близкими массами и близкими свойствами относительно сильных взаимодействий, Гейзенберг предложил рассматривать их как одно состояние - нуклон, в некотором гипотетическом пространстве, которое он назвал "изотопическим". Определим нуклон как состояние с двумя проекциями - протоном и нейтроном, проводя практически полную аналогию с введением спина 1/2 в обычном пространстве:

Такая запись означает, что протон и нейтрон определены как

,

Нуклон в изопространстве преобразуется с помощью 2-мерных эрмитовых матриц Паули tau1.gif (59 bytes)k, k = 1, 2, 3 или их линейных комбинаций,,

,,.

Диагональная матрица tau1.gif (59 bytes)3/2 - суть оператор 3-ей проекции изоспина:

,            

В изотопическом пространстве можно перевести протон (нейтрон) в нейтрон (протон) матрицами :

(6)

Подобно рассмотренному случаю с электроном,   напишем лагранжиан для свободного нуклонного поля:

(7)

Этот лагранжиан инвариантен относительно глобального калибровочного преобразования в изотопическом пространстве, которое задается унитарной 2-мерной матрицей, переводящей спинор N в N'. Эту матрицу удобно выбрать в виде экспоненты от 2-мерной эрмитовой матрицы, заданной произвольной линейной комбинацией матриц Паули tauk, k = 1, 2, 3:

psi'N(x) = UpsiN(x),  U = , 

(8)

где - три произвольные вещественные фазы. Такие 2 x 2 унитарные матрицы U образуют
группу SU(2). (Преобразование в (8) уже неабелево, поскольку задается экспонентой от 2-мерных матриц, некоммутирующих между собой и удовлетворяющих перестановочным соотношениям |τi,τj| = 2iεijkτk, i,j,k = 1,2,3). Обычно подразумевается, что как только сделан выбор, что называть протоном, а что нейтроном в одной точке пространства-времени, свобода выбора в других точках пространства-времени пропадает.  В то же время в отсутствие электромагнитного взаимодействия разделение нуклонов на   протоны и нейтроны совершенно произвольно. Поэтому представляется разумным ввести в фазы зависимость от   пространственно-временных координат.
    В соответствии с этим будем строить теперь калибровочную теорию, исходя из , потребовав инвариантности искомого лагранжиана относительно локального калибровочного преобразования в изотопическом пространстве:

psi'N(x) = psi><sub>N</sub>(x)<font SIZE=  = UpsiN(x).

(9)

Первоначальный неинвариантен относительно подобного локального калибровочного преобразования:

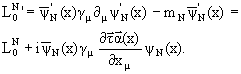
Аналогично предыдущему случаю, попытаемся скомпенсировать члены, нарушающие калибровочную инвариантность. Здесь их уже три, поскольку. Введем поэтому изотриплет векторных полей с калибровочным преобразованием

(10)

где U = . Взаимодействие этого изовекторного векторного поля с нуклоном зададим лагранжианом

(11)

где - константа связи нуклонов с ρ-мезонами, ,  . Соответствующие фейнмановские диаграммы имеют вид:

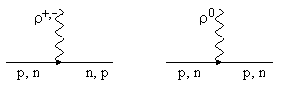
Рис. 2

Массу этого поля мы ввести не можем, как и в случае с фотоном, поскольку очевидным образом массовый член в лагранжиане неинвариантен относительно выбранного калибровочного преобразования (10) для поля . Запишем окончательное выражение для лагранжиана, инвариантного относительно локальных калибровочных преобразований неабелевой группы SU(2) (матрицы U в (8) как раз и образуют группу преобразований SU(2)):

где - тензор свободного безмассового ρ-мезонного поля:

   a,b,c = 0

который следующим образом ведет себя при калибровочных преобразованиях: , откуда следует, что
   Итак, требование независимости искомого лагранжиана относительно поворотов изоспина во всех точках пространства-времени привело к появлению безмассового изовекторного векторного поля с квантовыми числами ro-мезона, взаимодействующего с  изотриплетом нуклонных токов . В отличие от фотона, который не имеет заряда, введенное ρ-мезонное поле несет изотопический спин. В результате   тензор этого поля оказывается нелинейным по полю, что ведет к появлению самодействия. На диаграммном языке - появляются вершины с 3 и 4 ρ-мезонными линиями:

Рис.3

Этот формализм Гелл-Манном и Сакураи был обобщен на  SU(3)f, где вместо нуклонного изодублета в лагранжиане стоит барионный октет. Требование локальной калибровочной инвариантности относительно группы ароматов SU(3)f приводит к появлению октета безмассовых векторных мезонов с квантовыми числами известного октета мезонов 1-.
    К сожалению, на этом пути не удалось построить теории сильных взаимодействий с векторными мезонами в качестве квантов сильного поля. Но был создан формализм, позволивший решить эту задачу уже не в пространстве ароматов с группой калибровочной симметрии SU(3)f, а в пространстве цветов с группой калибровочной симметрии SU(3), где квантами поля оказались безмассовые векторные бозоны, несущие цвет - глюоны.

Упражнения

  1. Показать, что матрицы Паули удовлетворяют перестановочным соотношениям
    |τi,τj| = 2iεijkτk i, j, k = 1, 2, 3.
  2. Вычислить соотношения τ+p, τ-n.
  3. Показать, что .
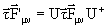  4. Показать, что выражение 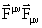инвариантно относительно локального калибровочного преобразования (9).

Содержание Продолжение

На головную страницу
Top.Mail.Ru