©hoo$e ЛAнg?Age©///?Ang?Age® Ekohomei©A TALKiNg ?.?.м.?.

geo.rf.gd

   

3. Фотон как калибровочное поле

    Но оказывается, что существование фотона может быть истолковано как проявление локальной калибровочной инвариантности лагранжиана, описывающего свободное поле заряженного фермиона спина 1/2, например, электрона. В некотором смысле природа может быть устроена так, что первичными оказываются свободные заряженные частицы полуцелого спина, а условие локальной калибровочной инвариантности, которое накладывается на уравнения, описывающие их свободное движение, вызывает к жизни векторное безмассовое поле, которое отождествляется с электромагнитным  полем.
    В качестве заряженной частицы выберем электрон. Уравнение Дирака, описывающее свободное движение электрона (∂νγν – me)ψe(х) = 0, может быть получено из лагранжиана

(3)

с помощью уравнения Лагранжа-Эйлера вида

.

Введем операцию калибровочного (или градиентного) преобразования над волновой функцией электрона ψе, которое сводится к умножению на eiα:

где α-произвольное вещественное число.
    Лагранжиан L0 очевидным образом инвариантен относительно калибровочного преобразования волновой функции электрона такого вида. Это так называемое глобальное калибровочное преобразование, так как оно задается во всем пространстве-времени (-число!). Это преобразование абелево, что означает, что два преобразования такого типа коммутируют между собой:. (В противном случае преобразование именуется неабелевым.) Поскольку в квантовой механике и в квантовой теории поля все наблюдаемые величины связаны с билинейными комбинациями вида , изменение фазы никак на них не влияет.
    Но возникает вопрос, не является ли более последовательным определять изменение фазы локально, т.е. задавать свою фазу в каждой точке пространства-времени x некоторой функцией (x). Ведь все поля в теории поля определены как функции x в 4-пространстве Минковского. Естественно при этом потребовать инвариантности искомого лагранжиана относительно такого локального калибровочного преобразования, когда является функцией x:

(4)

Но лагранжиан L0', полученный из исходного L0, если его записать через штрихованные волновые функции, неинвариантен относительно этого локального калибровочного преобразования:

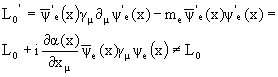
Однако можно попытаться добиться того, что искомый лагранжиан будет-таки инвариантен относительно локального калибровочного преобразования (4). Для этого нужно найти способ   убрать член , нарушающий калибровочную инвариантность. Введем некоторое векторное поле Аμ, которое при калибровочном преобразовании волновой функции электрона (4) имеет калибровочное преобразование вида

.

Взаимодействие этого векторного поля с электроном зададим лагранжианом

(Он имеет тот же вид, что и лагранжиан взаимодействия фотона с электроном (2).) Заменяя в этом лагранжиане все поля на штрихованные, получим

Итак, сумма L0 + Lint = L'0 + L'int оказывается инвариантной относительно локального калибровочного преобразования (4). Массу этого поля при требовании инвариантности полного лагранжиана относительно выбранных калибровочных преобразований мы ввести тем не менее не можем, поскольку очевидным образом массовый член в лагранжиане неинвариантен относительно выбранного калибровочного преобразования для поля Аμ:

Введенное безмассовое векторное поле по квантовым числам совпадает с электромагнитным. Попытаемся поэтому отождествить это поле Аμ с электромагнитным полем Аμ и запишем окончательное выражение для полного лагранжиана, инвариантного относительно выбранных локальных калибровочных преобразований (4):

(5)

где члены в квадратной скобке описывают свободное движение электрона массы me, член   описывает свободное электромагнитное поле, а последний член - взаимодействие электрона с электромагнитным полем. В итоге мы получили те же выражения, что и раньше, для описания взаимодействия электрона и фотона. Однако, смысл полученных выражений другой. Фотон появляется не как самостоятельное фундаментальное поле, никак не связанное с электроном, а как некоторое компенсирующее поле, введенное чтобы получить теорию свободного электрона, инвариантную относительно локальных калибровочных преобразований абелевой группы U(1). (Это группа, элементами которой как раз и  являются вращения на произвольные углы вокруг одной оси.)
    Для теории квантовой электродинамики оба подхода в сущности эквивалентны и, естественно, приводят к одинаковым результатам.
    Но калибровочные пребразования дают нам принцип построения физических теорий, далеко выходящий за рамки введения феноменологических полей для описания того или иного взаимодействия.
    1. В калибровочных теориях из условия инвариантности лагранжиана относительно различных локальных калибровочных преобразований возникают векторные поля, лежащие в основе сильных, электромагнитных и   слабых взаимодействий между всеми фундаментальными частицами.
    2. Калибровочные теории обладают важным свойством перенормируемости, что означает, что они приводят к корректным выражениям во всех порядках теории возмущений. Поэтому можно быть уверенным, что полученные на их основе модели непротиворечивы. (К сожалению, без введения в квантовую теорию поля мы не можем   пояснить этот пункт подробнее.)
    Именно поэтому требование инвариантности лагранжиана относительно локальных калибровочных преобразований оказывается исходным принципом построения всех современных теорий микромира.

     Упражнение

     Показать, что тензор электромагнитного поля инвариантен относительно локальных калибровочных преобразований (4).

Содержание Продолжение

На головную страницу
Top.Mail.Ru