В качестве первого и относительно простого примера рассмотрим электромагнитное взаимодействие. Со времени создания Максвеллом теории электромагнитного поля принимается, что существует собственно электромагнитное поле, описываемое в классической электродинамике 4-вектором ,
где φ(x) - скалярный, а (x) - векторный потенциал электромагнитного поля, которое связано с измеряемыми на опыте магнитным и электрическим полями соотношениями

= rot,     .

Уравнения Максвелла имеют вид

  ,       div= 0,
   ,    div= 4,

где ρ - плотность электрического заряда, j-плотность электрического тока. Уравнения Максвелла можно записать в 4-мерном виде:

∂_μF_μν = j_ν,

ε_αβμν∂_βF_μν = 0,     ∂_μA_μ = 0,

где F_μν - тензор электромагнитного поля такой что

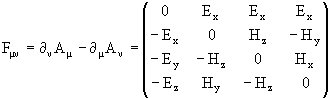
Здесь ε_αβμν - абсолютно асимметричный тензор 4-го ранга, его компоненты отличны от нуля только при значениях и меняют знак при перестановке любых двух индексов, ε₁₂₃₄ = 1. А j_ν = (ρ,) - 4-вектор плотности тока заряженных частиц. Для классической заряженной частицы заряда -e, движущейся со скоростью , = -e. Если, к примеру, это плотность тока электронов, описываемых волновой функцией ψ_е(х), которая подчиняется уравнению Дирака (∂_νγ_ν – m_e)ψ_e(х) = 0, γ_ν – матрицы Дирака, то она имеет вид:

    Взаимодействие фотонов с электронами задается лагранжианом

которому соответствует фейнмановская диаграмма

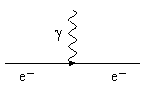
Рис. 1

В таком подходе фотон существует независимо и наряду с заряженными частицами, входя в фундаментальную вершину, лежащую в основе описания всех электромагнитных процессов в квантовой электродинамике. Как элементарная частица фотон представляет собой безмассовую векторную частицу - бозон со спином 1 и отрицательной внутренней четностью.