Основные свойства электромагнитного
взаимодействия предполагаются известными на
уровне обычных курсов физического факультета.
Предполагается, в частности, известным вид
лагранжиана взаимодействия электронов с
электромагнитным полем. Электромагнитный ток
отдельных барионов и кварков можно задать
совершенно аналогичным образом через лагранжиан
взаимодействия частицы заряда e, описываемой
спинорным полем ![]() (x), с
электромагнитным полем
(x), с
электромагнитным полем ![]() (x):
(x):
|
(3.1) |
(При этом мы пока рассматриваем барион как
точечный.)
Переход к унитарной симметрии
означает, что вместо ψ(x) для
каждого бариона, следует подставить теперь весь
октет целиком ![]() (x).
(x).
А каковы свойства электромагнитного
тока в унитарной симметрии? Поскольку
электромагнитный ток есть суперпозиция
изовектора и изоскаляра, и сам ток заряда не
несет, его можно связать с компонентой ![]() октета векторных токов
октета векторных токов ![]() . Часть тока, связанная с
электрическим зарядом, должна быть такой, чтобы
заряды частиц оказались правильными. Опуская
пространственные индексы, запишем
. Часть тока, связанная с
электрическим зарядом, должна быть такой, чтобы
заряды частиц оказались правильными. Опуская
пространственные индексы, запишем
|
(3.1) |
Здесь p = ![]() и т.д.-
октетная матрица барионов JP = 1/2+.
Легко видеть, что заряды барионов
воспроизводятся правильно. То же справедливо и
для мезонов.
и т.д.-
октетная матрица барионов JP = 1/2+.
Легко видеть, что заряды барионов
воспроизводятся правильно. То же справедливо и
для мезонов.
Рассмотрим в импульсном представлении
часть лагранжиана взаимодействия, связанную с
магнитным моментом,
|
(3.3) |
(в импульсном представлении при выборе ![]() = (0,0,k3),
= (0,0,k3), ![]() = -k3
= -k3![]() 2,
2, ![]() = k3
= k3![]() 1,
1, ![]() = 0. Когда же мы хотим определить
магнитный момент по взаимодействию частицы с
внешним магнитным полем, обычно выбираем
систему, в которой
= 0. Когда же мы хотим определить
магнитный момент по взаимодействию частицы с
внешним магнитным полем, обычно выбираем
систему, в которой ![]() = (0,0,H3).)
= (0,0,H3).)
Эта та часть магнитного момента,
которая обычно именуется нормальным магнитным
моментом, присущим частицам спина 1/2, чьи
волновые функции удовлетворяют уравнению
Дирака.
Но есть еще одна структура Лоренца,
которая приводит к аналогичному конечному
выражению в нерелятивистском пределе:
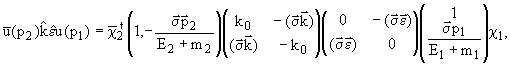
![]()
(![]() )
)
Эта часть магнитного момента частицы
обычно именуется аномальным магнитным моментом,
для заряженных адронов соразмерного с величиной
нормального магнитного момента, так что полный
магнитный момент есть для них сумма этих двух
моментов, а для нейтральных составляет полный
магнитный момент частицы.
При построении октета барионного тока
из произведения октетов барионов и антибарионов
(с произвольной пространственной структурой
тока!), возможны, как мы уже знаем, две различные
унитарные тензорные структуры (что
соответствует наличию двух октетов в разложении
|
(3.5) |
причем ![]() = 0,
α, β,
γ, η =1,2,3, и
тогда электромагнитный ток (мы опускаем
пространственные индексы) запишется как
= 0,
α, β,
γ, η =1,2,3, и
тогда электромагнитный ток (мы опускаем
пространственные индексы) запишется как
|
(3.6) |
В результате для магнитных моментов барионов получим:
μ(p)
= F + frac{1}{}D/3, |
(3.7) |
(Напомним, что здесь ![]() = p.)
Во многих современных моделях именно этими
формулами задаются лидирующие вклады в
магнитные моменты барионов, к которым затем
добавляются вклады, рассчитываемые часто в
рамках очень сложных теоретических построений.
= p.)
Во многих современных моделях именно этими
формулами задаются лидирующие вклады в
магнитные моменты барионов, к которым затем
добавляются вклады, рассчитываемые часто в
рамках очень сложных теоретических построений.
А как построить электромагнитный ток
кварков?
|
(3.8) |
где в квадратных скобках выделен
электромагнитный ток 3-х кварковой модели.
А как здесь решить задачу построения
тех же магнитных моментов барионов октета? Для
этого придется в явном виде расписать барионные
волновые функции через кварковые. В модели SU(3)f-симметрии
:
![]()
Тогда в нерелятивистском пределе магнитный
момент бариона будет суммой вкладов магнитных
моментов кварков, а оператор магнитного момента
кварка q есть просто ![]() (кварк, на который действует оператор магнитного
момента, будем отмечать звездочкой *).
(кварк, на который действует оператор магнитного
момента, будем отмечать звездочкой *).
|
(3.9) |
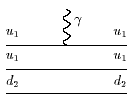
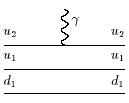
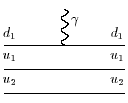
где воспользовались тем, что два кварка из трех-спектаторы, так что
<u1u1d2|![]() |u*1u1d2> = <u1|
|u*1u1d2> = <u1|![]() |u*1>=
|u*1>=![]() u etc.
u etc.
Соответствующие кварковые диаграммы можно записать как (приведена только часть из них, остальные сразу можно написать, исходя из подробно выписанного выше матричного элемента):
 |
 |
 |
Подобным образом можно получить в рамках кварковой модели магнитный момент нейтрона:
μn
= ![]() q=u,s<n
q=u,s<n![]() |
|![]() |n
|n![]() > =
> =
=![]() <2d1d1u2
- d1u1d2 - u1d1d2|
<2d1d1u2
- d1u1d2 - u1d1d2| ![]() |2d1d1u2 - d1u1d2
- u1d1d2> =
|2d1d1u2 - d1u1d2
- u1d1d2> =
=![]() μd -
μd - ![]() μu,
μu,
магнитный момент гиперона Σ+:
μ(Σ+) = ![]() q=u,d<
q=u,d<![]() +
+![]() |
|![]() |
|![]() +
+![]() > =
> =
=![]() <2u1u1s2
- u1s1u2 - s1u1u2|
<2u1u1s2
- u1s1u2 - s1u1u2|![]() |2u1u1s2 - u1s1u2
- s1u1u2> =
|2u1u1s2 - u1s1u2
- s1u1u2> =
=![]() μu -
μu - ![]() μs,
μs,
магнитный момент гиперона Σ-:
μ(Σ-) = ![]() q=u,d<
q=u,d<![]() -
-![]() |
|![]() |
|![]() -
-![]() > =
> =
=![]() <2d1d1s2
- d1s1d2 - s1d1d2|
<2d1d1s2
- d1s1d2 - s1d1d2|![]() |2d1d1s2 - d1s1d2
- s1d1d2> =
|2d1d1s2 - d1s1d2
- s1d1d2> =
=![]() μd -
μd - ![]() μs,
μs,
магнитный момент гиперона ![]() (получение которого мы выпишем
подробнее из-за того, что он имеет волновую
функцию другого вида) :
(получение которого мы выпишем
подробнее из-за того, что он имеет волновую
функцию другого вида) :
|
+ s1u*1d2 - s1u1d*2
- d*1s1u2 - d1s*1u2 + d1s1u*2
- s*1d1u2 - s1d*1u2 + s1d1u*2>
= |
(3.10) |
магнитный момент каскадного гиперона Ξ0:
μ(Ξ0) = ![]() q=u,s<Ξ0
q=u,s<Ξ0![]() |
|![]() |Ξ0
|Ξ0![]() > =
> =
=![]() <2s1s1u2
- s1u1s2 - u1s1s2|
<2s1s1u2
- s1u1s2 - u1s1s2|![]() |2s1s1u2 - s1u1s2
- u1s1s2> =
|2s1s1u2 - s1u1s2
- u1s1s2> =
=![]() μs -
μs - ![]() μu,
μu,
и магнитный момент каскадного гиперона Ξ-:
μ(Ξ-) = ![]() q=d,s<Ξ-
q=d,s<Ξ-![]() |
|![]() |Ξ-
|Ξ-![]() > =
> =
=![]() <2s1s1d2
- s1d1s2 - d1s1s2|
<2s1s1d2
- s1d1s2 - d1s1s2|![]() |2s1s1d2 - s1d1s2
- d1s1s2> =
|2s1s1d2 - s1d1s2
- d1s1s2> =
=![]() μs -
μs - ![]() μd.
μd.
Здесь q1 = q![]() , q2 = q
, q2 = q![]() , q =
u,d,s,c,b,t.
, q =
u,d,s,c,b,t.
Для примера приведем некоторые результаты теоретических расчетов магнитных моментов барионов и соответствующие экспериментальные данные.
| μ(B) в из [2] |
μ(B) в
μN из [3] |
μ(B) в
μN из [4] |
μ(B) в
μN из [5] |
μ(B) в
μN из [6] |
2.69 |
2.78 |
2.75 |
2.793 |
2.79 |
-1.85 |
-1.86 |
-1.84 |
-1.69 |
-1.91 |
2.59 |
2.50 |
2.69 |
2.481 |
2.43 |
-1.22 |
-1.215 |
-0.98 |
-1.155 |
-1.15 |
-0.61 |
-0.6397 |
-0.66 |
-0.6507 |
-0.66 |
-1.33 |
-1.244 |
-1.58 |
-1.274 |
-1.25 |
-0.59 |
-0.631 |
-0.72 |
-0.604 |
-0.64 |
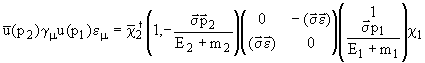
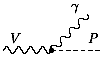 Обратимся к
радиационным распадам векторных мезонов V
Обратимся к
радиационным распадам векторных мезонов V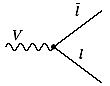 Построим
теперь в рамках унитарной симметрии
электромагнитный ток, описывающий лептонные
распады векторных мезонов V
Построим
теперь в рамках унитарной симметрии
электромагнитный ток, описывающий лептонные
распады векторных мезонов V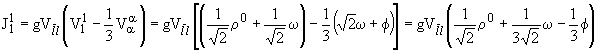 .
.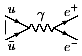 -
- 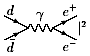 =
= 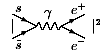 =
=