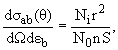Сечение ядерной реакции - величина характеризующая вероятность перехода системы двух взаимодействующих частиц в определенное конечное состояние.
   Вероятность ядерного взаимодействия принято определять через эффективную площадь ядра , находящегося на пути пучка. Обозначим число частиц упавших на единичную площадь мишени, расположенную перпендикулярно оси пучка через N₀. Пусть на этой площади находится n ядер. Тогда число взаимодействий определяется соотношением

N = N0n,

(3.1)

где называется полным сечением.
Количество частиц мишени на единицу площади можно рассчитать, если известна толщина мишени

,

(3.2)

где ρ − плотность вещества мишени, d − толщина мишени, N_A − число Авогадро, А − массовое число.
    Сечение реакции может отличаться от геометрической площади сечения ядра на несколько порядков.
   Сечения реакций определенного типа (например (p,n), (p,d) и.т.д.) называются парциальными сечениями. Часто в данной реакции выделяют сечения процессов приводящих к возбуждению различных состояний конечных ядер. Такие сечения также называют парциальными. Полное сечение реакций складывается из парциальных сечений различных реакций, возможных при данной энергии.

σ = ∑σ_b,

где σ_b − парциальные сечения реакции.
   За единицу сечения принят 1 барн = 10^-24 см².
   В зависимости от поставленной задачи и условий эксперимента используют также понятия интегрального, дифференциального и дважды дифференциального сечений реакции.
Дважды дифференциальным сечением реакции a + A → b + B называется величина

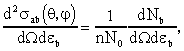(3.3)

где n - количество частиц мишени на единицу площади, N₀ − количество попавших на мишень частиц a, dN_b/dΩdε_b − количество частиц, продуктов данной реакции b, вылетевших в элемент телесного угла dΩ в направлении, характеризуемом полярным и азимутальным φ углами, и имеющих энергию в диапазоне ε_b ÷ (ε_b + dε_b).
    При исследованиях ядерных реакций измерение дважды дифференциальных сечений является самым распространенным типом эксперимента. Упрощенная схема экспериментальной установки для измерения дважды дифференциальных сечений в реакциях с заряженными частицами показана на рисунке.

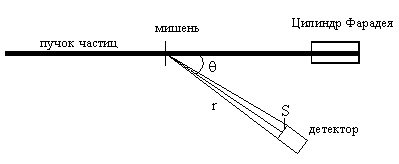
На неполяризованную тонкую мишень падает неполяризованный пучок частиц фиксированной энергии. Продукты реакции регистрируются детектором с апертурой S, который расположен на растоянии r от мишени и под углом θ от направления пучка. В этом случае дважды дифференциальное сечение зависит только от  угла θ и определяется из соотношения

где N_i - количество зарегистрированных детектором за время измерения частиц-продуктов реакции b, имеющих энергию в диапазоне ε_b ÷ (ε_b + dε_b). N₀ - количество упавших на мишень  частиц a. При измерениях на тонкой мишени N₀ обычно определяют, измеряя заряд частиц пучка попавших за время измерения в так называемый цилиндр Фарадея. В случае тонкой мишени доля частиц пучка вступивших в реакции с частицами мишени и в результате выбывших из пучка весьма мало (10^-5-10^-6).

Дифференциальными сечениями реакции называются величины:

	(3.5)
,	(3.6)

Дифференциальное сечение упругого рассеяния в кулоновском поле ядра определяется формулой Резерфорда

,

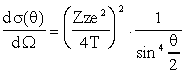(3.7)

  где Z и z − заряды ядра и налетающей частицы в единицах заряда электрона e, T − кинетическая энергия налетающей частицы, θ − угол рассеяния.

Интегральным сечением реакции называется величина:

.

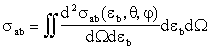(3.8)

  Интегральные сечения реакции a + A → b + B σ_ab и обратной реакции b + B → a + A σ_ba связаны между собой принципом детального равновесия:

(3.9)

где j_a, j_A, j_b, j_B спины, а _a и _b импульсы частиц в системе центра инерции.
    В случаях , когда в реакции участвует γ-квант необходимо учесть, что для него множитель 2j + 1 = 2, так как спин γ-кванта имеет 2 проекции.

ЗАДАЧИ