Радиус атомного ядра можно оценить, если известна дифракционная картина рассеяния заряженных частиц на этом ядре. Этот метод использует волновые свойства падающих на ядро частиц. Из классической оптики известно, что для наблюдения дифракционной картины на некотором объекте ограниченных размеров необходимы два условия: 1) длина падающей на объект волны λ должна быть порядка или меньше радиуса объекта (λ ≤ R) и 2) объект должен иметь довольно чёткие границы (толщина поверхностного слоя объекта не должна заметно превышать его общие размеры).

Рис. 1. Рассеяние волны на круглом объекте радиуса R (слева) и дифракционная
картина, наблюдаемая на экране (справа)
Если эти условия выполнены, то на экране, расположенном за ядром-рассеивателем (рис. 1.), должны наблюдаться центральный самый мощный дифракционный максимум и при увеличении угла рассеяния θ − серия уменьшающихся максимумов, разделенных минимумами. Если рассеяние происходит на круглом объекте, то угол θmin, под которым будет виден первый дифракционный минимум, может быть найден из следующего приближённого выражения:
|
|
(1) |
Полное сечение реакции и радиус ядра
При достаточно высоких энергиях сталкивающихся частиц,
когда
![]() << R,
полное сечение реакций стремится к πR2.
<< R,
полное сечение реакций стремится к πR2.
| σtot = πR2. | (2) |
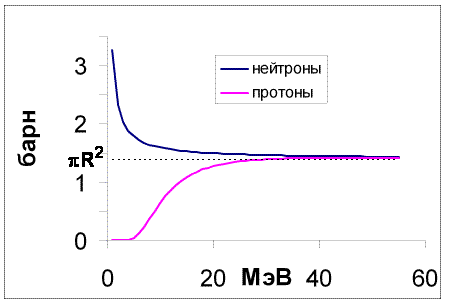
Рис. 2. Зависимость полных сечений реакций на
120Sn от энергии налетающей частицы
Таким образом, для определения радиусов атомных ядер можно
использовать прохождение коллимированного потока моноэнергетических частиц через
тонкие мишени, состоящие из исследуемых ядер.
Если на тонкую пластинку вещества толщиной x нормально к её
поверхности падает узкий пучок моноэнергетических частиц с плотностью потока j(0),
то при условии не более чем однократного взаимодействия каждой из этих частиц с
ядрами мишени плотность потока за мишенью будет даваться соотношением
| j(х) = j(0)exp(-nσtotx), | (3) |
где n - концентрация ядер мишени, а σtot полное эффективное сечение взаимодействия падающих частиц с ядром. Тогда
| j(х) = j(0)exp(-nσtotx), | (4) |
|
|
(5) |
Здесь использовано, что n = ρNA/A, где ρ плотность мишени, NA - число Авогадро и А - массовое число. Окончательно для величины радиуса ядра имеем
| R = (σtot/π)1/2. | (6) |