Большинство наблюдаемых частиц является частицами
нестабильными. Скорость распада характеризуется такими связанными между собой
величинами как постоянная распада
λ, среднее время жизни τ,
период полураспада T1/2 и
ширина распада Г.
Если в начальный момент времени t = 0 число распадающихся
частиц составляло N(0), то к моменту времени t число нераспавшихся частиц N(t)
определяется соотношением
| N(t) = N(0)exp(-λt), | (1) |
где λ - постоянная распада.
Постоянная распада - вероятность
распада частицы в единицу времени.
Волновая функция ψ(t) покоящейся частицы (p = 0) с энергией
состояния E описывается соотношением
| ψ(t) = ψ(0)exp(-iEt/ћ). | (2) |
Если энергия состояния E является действительной величиной, то вероятность нахождения частицы в данном состоянии не будет зависеть от времени, так как
| |ψ(t)|2 = |ψ(0)|2. | (3) |
Т.е. частица описываемая волновой функцией (2) с действительным значением энергии является стабильной. Соотношение (2) описывает станционарное состояние. У нестабильного состояния энергия является комплексная величина
| E = E0 - iГ/2. | (4) |
Тогда вероятность найти частицу в состоянии с энергией E = E0 - iГ/2 в момент времени t будет определяться соотношением
| |ψ(t)|2 = |ψ(0)|2exp(-iГ/ћ), | (5) |
что согласуется с законом радиоактивного распада (1). При этом Г/![]() = λ характеризует вероятность распада нестанционарного состояния. Смысл величины
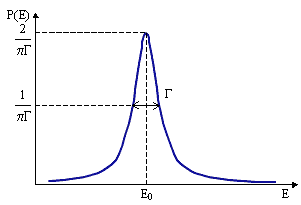
Г легко понять, если представить распадающееся состояние с помощью
Фурье-преобразования не как функцию времени ψ(t), а как функцию энергии Р(Е)
= λ характеризует вероятность распада нестанционарного состояния. Смысл величины
Г легко понять, если представить распадающееся состояние с помощью
Фурье-преобразования не как функцию времени ψ(t), а как функцию энергии Р(Е)
| (6) |
 Т.е.
энергия распадающегося состояния характеризуется не только величиной E0,
но и шириной Г, описывающей скорость распада состояния. Чем больше ширина
состояния Г, тем больше вероятность распада λ и тем меньше
среднее время жизни τ распадающегося состояния, т.к.
Т.е.
энергия распадающегося состояния характеризуется не только величиной E0,
но и шириной Г, описывающей скорость распада состояния. Чем больше ширина
состояния Г, тем больше вероятность распада λ и тем меньше
среднее время жизни τ распадающегося состояния, т.к.
τ = 1/λ = ћ/Г.
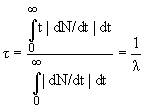 . . |
(7) |
Период полураспада T1/2 - время, за которое первоначальное количество частиц уменьшается в два раза
| T1/2 = ln2/λ = 0.693/λ = τln2. | (8) |

