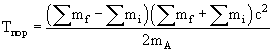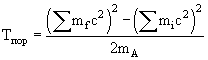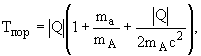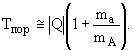Энергия реакции это кинетическая энергия выделяющаяся или поглощающаяся в процессе реакции; она равна разности энергий покоя частиц в начальном и конечном состояниях. В общем случае, когда в конечном состоянии больше двух частиц энергия реакции определяется формулой
|
(1) |
где mi и mf - массы частиц в
начальном и конечном состоянии. Реакции с
Q > 0 называются экзотермическими,
они идут с выделением знергии при любой энергии
налетающей частицы. Реакции с Q < 0
называются эндотермическими.
В реакциях упругого рассеяния Q = 0. Для того
чтобы была возможна эндотермическая реакция,
необходимо чтобы энергия налетающей частицы
превышала некоторую величину Tпор,
называемую порогом реакции.
Порог реакции
это минимальная кинетической энергии налетающей
частицы в лабораторной системе координат, при
котором возможна данная реакция.
|
(2a) |
где mi и mf − массы частиц в начальном и конечном состоянии, mA − масса мишени
или
|
(2б) |
или
|
(2в) |
где Q – энергия реакции, ma
– масса
налетающей частицы, mA – масса ядра мишени.
В нерелятивистском приближении (Q<< 2mAc2)
|
(2г) |
Отметим, что соотношения (2)
справедливы и для реакций с любым количеством
частиц в конечном состоянии.
Из соотношений (2)
видно, что порог реакции не совпадает с энергией
реакции. Из самого смысла величины Q видно,
что Q есть порог ядерной реакции в системе центра
инерции. Поэтому порог ядерной реакции Tпор
всегда больше энергии реакции Q на величину
энергии связанной с движением центра инерции в
лабораторной системе координат. В ускорителях с
неподвижной мишенью значительная часть энергии
пучка тратится на бесполезную энергию движения
центра инерции. Поэтому в физике высоких энергий,
где такие потери были бы особенно велики, а выбор
партнера столкновения не столь существенный, как
в физике ядра, используют ускорители
на встречных пучках (коллайдеры). Если
использовать для столкновений частицы равных
масс m, то для реализации реакции с данным Q
необходимы встречные пучки с кинетическими
энергиям T' каждого из пучков,
| T' = |Q/2|. | (3) |
Для реализации этой же реакции на ускорителе с неподвижной мишенью энергия пучка должна была бы быть, как это видно из (2) и (3)
| Tэкв = 2T'(T' + 2mc2)/mc2. | (4) |
или для полных энергий Е и Е'
| Еэкв = 2Е'2/mc2 – mc2 ≈ 2Е'2/mc2. | (5) |
Ускорители имеющие одинаковые полезные
энергии называются эквивалентными.
Существуют ускорители на встречных
пучках, в которых ускоряются частицы разной
массы. Максимальная масса частиц M, которая может
быть рождена на таком ускорителе рассчитывается
с помощью соотношения
| Мc2 = 2(TaTb)1/2, | (6) |
где Ta и Tb - кинетические энергии встречных пучков.
См. также Реакции с ядрами и частицами
21.11.16