Открытие большого количества частиц, исследование механизмов их взаимодействий и распадов привело к необходимости введения новых характеристик частиц - новых квантовых чисел. Были открыты новые особенности различных взаимодействий и, в частности, новые свойства симметрии.
    Важную роль в понимании механизмов взаимодействия элементарных частиц, их образования и распада сыграли законы сохранения. Законы сохранения определяют правила отбора, согласно которым процессы с частицами, приводящие к нарушению законов сохранения, не могут осуществляться в определенных типах взаимодействий. В дополнение к законам сохранения, действующим в макромире, в физике микромира были обнаружены новые законы сохранения, позволяющие объяснить наблюдаемые экспериментальные закономерности.
    Законы сохранения являются результатом обобщения экспериментальных наблюдений. Часть из них была открыта в результате того, что реакции или распады, разрешенные всеми ранее известными законами сохранения, не наблюдались или оказывались сильно подавленными. Так были открыты законы сохранения барионного, лептонных зарядов, странности, чарма и др.
    Как известно из классической механики производная от некоторой механической величины F может быть выражена через классическую скобку Пуассона

Переходя от классических величин к квантовым, получим

Отсюда следует, что квантовомеханическая величина является интегралом движения если

1. Оператор 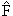не зависит от времени явно.
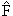2. Оператор коммутирует с оператором Гамильтона.

В этом случае

Это легко получить из следующих простых вычислений.

Выразив производные /t и */t  через волновые функции с помощью уравнения Шредингера

И комплексно сопряженного с ним уравнения

В соотношении (7) учтено, что оператор Ĥ - эрмитов.
    Таким образом, из соотношения (3) следует, что если известны операторы различных квантовомеханических величин и оператор Гамильтона системы, можно найти величины сохраняющиеся в процессе движения системы.
    В каждом случае, когда физические законы инвариантны относительно какой-либо операции симметрии U, существует соответствующая ей сохраняющаяся физическая величина.
    Законы симметрии устанавливаются на основе эксперимента.
    Оператор , описывающий определённую симметрию системы, должен коммутировать с Гамильтонианом, описывающим систему

Ĥ - Ĥ = 0.

1. Требование независимости законов движения системы от выбора начала отсчёта времени выражается в коммутации оператора трансляции на малый интервал времени (δt)

(δt) = 1 + δt·∂/∂t

с оператором Гамильтона

(δt) = Ĥ(δt)

что приводит к закону сохранения энергии в замкнутой системе или системе в стационарных внешних полях.

2. Сохранение момента количества движения связано с изотропией пространства. Оператор Ŵ_z поворота на малый угол δφ вокруг оси z связан с _z - проекцией вектора оператора момента соотношением

Ŵ_z = 1 + (i/)δφ·_z.

Следствием коммутации операторов Ŵ_z   с оператором Гамильтона является закон сохранения момента количества движения. Учёт квантовых закономерностей приводит к двум важным следствиям.

1. Момент количества движения J квантуется.
2. Частица может иметь собственный момент количества движения - спин s

= + .

3. Сохранение импульса связано с однородностью пространства. Из однородности пространства следует, что оператор сдвига _x в направлении х

_x = 1 + (i/)Δx_x

не должен изменять гамильтониан замкнутой системы, т.е. должен коммутировать с ним.

Ĥ_x - _xĤ = 0.

    Установлено, что каждый закон сохранения связан с какой-либо симметрией в окружающем нас мире (теорема Нетер). Так законы сохранения энергии и импульса связанны с однородностью времени и пространства. Закон сохранения момента количества движения связан с симметрией пространства относительно вращений. Законы сохранения зарядов связаны с симметрией физических законов относительно специальных преобразований, описывающих частицы.
     Информация о том, какие величины сохраняются в различных взаимодействиях, приведена в таблице. Знак "+" ("-") показывает, что данная величина сохраняется (не сохраняется). В аддитивных законах сохраняется сумма величин, в мультипликативных законах - произведение величин, которые могут быть равны +1 или -1.
    В результате действия законов сохранения, протон и антипротон - стабильные частицы, т.к. являются самыми легкими частицами, имеющими барионные заряды B = 1 и B = -1 соответственно. Стабильными частицами являются также электрон и позитрон, т.к. это самые легкие частицы, имеющие электрический заряд Q = -1 и Q = 1 соответственно. Также являются стабильными частицами нейтрино и антинейтрино, т.к. это самые легкие носители лептонных зарядов L_e, , .

ЗАДАЧИ

17.11.15