| Qα = ( M(A,Z)
- M(A-4,Z-2) - Mα ) с2 + |
(3) |
©hoo$e ЛÄнgიAge©///₾ÄngიAge® Ekohomei©Å TÅLKiNg ი.ბ.м.ლ.
Альфа-распад
- распад атомных ядер, сопровождающийся испусканием альфа-частиц (ядер 4He).
Часть изотопов могут самопроизвольно испускать альфа-частицы
(испытывать альфа-распад), т.е. являются
альфа-радиоактивными. Альфа-радиоактивность за редким
исключением (например 8Be) не встречается среди легких и средних
ядер. Подавляющее большинство альфа-радиоактивных изотопов (более 200)
расположены в периодической системе в в области тяжелых ядер (Z > 83). Известно
также около 20 альфа-радиоактивных изотопов среди редкоземельных элементов,
кроме того, альфа-радиоактивность характерна для ядер, находящихся вблизи
границы протонной стабильности. Это обусловлено тем, что альфа-распад связан с
кулоновским отталкиванием, которое возрастает по мере увеличения размеров ядер
быстрее (как Z2 ), чем ядерные силы притяжения, которые растут
линейно с ростом массового числа A.
Ядро альфа-радиоактивно, если выполнено условие, являющееся
следствием закона сохранения энергии
| M(A,Z) >M(A-4,Z-2) + Mα, | (1) |
где M(A,Z) и M(A-4,Z-2) - массы покоя исходного и конечного ядер соответственно, Mα - масса альфа-частицы. При этом в результате распада конечное ядро и альфа-частица приобретают суммарную кинетическую энергию
| Qα = ( M(A,Z) - M(A-4,Z-2) - Mα ) с2, | (2) |
которая называется энергией альфа-распада. Ядра могут испытывать альфа-распад также на возбужденные состояния конечных ядер и из возбужденных состояний начальных ядер. Поэтому соотношение для энергии альфа-распада (2) можно обобщить следующим образом
| Qα = ( M(A,Z)
- M(A-4,Z-2) - Mα ) с2 + |
(3) |
где ![]() и
и ![]() - энергии возбуждения начального и
конечного ядер соответственно. Альфа-частицы, возникающие в результате распада
возбужденных состояний, получили название
длиннопробежных. Для большинства ядер с A > 190 и для многих
ядер с 150 < A < 190 условие (12) выполняется, однако далеко не все они
считаются альфа-радиоактивными. Дело в том, что современные экспериментальные
возможности не позволяют обнаружить альфа-радиоактивность для нуклидов с
периодом полураспада большим, чем 1016 лет. Кроме того, часть
“потенциально” альфа-радиоактивных ядер испытывают также бета-распад, который
сильно конкурирует с альфа-распадом.
- энергии возбуждения начального и
конечного ядер соответственно. Альфа-частицы, возникающие в результате распада
возбужденных состояний, получили название
длиннопробежных. Для большинства ядер с A > 190 и для многих
ядер с 150 < A < 190 условие (12) выполняется, однако далеко не все они
считаются альфа-радиоактивными. Дело в том, что современные экспериментальные
возможности не позволяют обнаружить альфа-радиоактивность для нуклидов с
периодом полураспада большим, чем 1016 лет. Кроме того, часть
“потенциально” альфа-радиоактивных ядер испытывают также бета-распад, который
сильно конкурирует с альфа-распадом.
Основную часть энергии альфа-распада (около 98%) уносят альфа-частицы. Используя
законы сохранения энергии и импульса для кинетической энергии альфа-частицы Tα
можно получить соотношение
|
(4) |
Периоды полураспада известных альфа-радиоактивных нуклидов
варьируются от 0.298 мкс для 212Po до
Важным свойством альфа-распада является то, что при небольшом
изменении энергии альфа-частиц периоды полураспада меняются на многие порядки.
Так у 232Th Qα = 4.08 МэВ, T1/2 = 1.41·1010
лет, а у 218Th Qα = 9.85 МэВ, T1/2 = 10 мкс.
Изменению энергии в 2 раза соответствует изменение в периоде полураспада на 24
порядка.
Для четно-четных изотопов одного элемента зависимость периода
полураспада от энергии альфа-распада хорошо описывается эмпирическим законом
Гейгера - Неттола
| lg T1/2 = A + B/(Qα)1/2, | (5) |
где A и B - константы слабо зависящие от Z. С учетом заряда дочернего ядра Z связь между периодом полураспада T1/2 и энергией альфа-распада Qα может быть представлено в виде (B.A. Brown, Phys. Rev. c46, 811 (1992))
| lg T1/2 = 9.54Z0.6/(Qα)1/2 - 51.37, | (6) |
где T1/2 в сек, Qα в МэВ. На рис. 1 показаны экспериментальные значения периодов полураспада для 119 альфа-радиоактивных четно-четных ядер (Z от 74 до 106) и их описание с помощью соотношения (6).
|
Для нечетно-четных, четно-нечетных и нечетно-нечетных ядер общая тенденция
сохраняется, но их периоды полураспада в 2 - 1000 раз больше, чем для
четно-четных ядер с данными Z и Qα.
Основные особенности альфа-распада, в частности сильную
зависимость вероятности альфа-распада от энергии удалось в 1928 г. объяснить
Г. Гамову и независимо от него
Р. Герни и
Э. Кондону. Ими было показано,
что вероятность альфа-распада в основном определяется вероятностью прохождения
альфа-частицы сквозь потенциальный барьер.
Рассмотрим простую модель альфа-распада. Предполагается, что
альфа-частица движется в сферической области радиуса R, где R - радиус ядра.
Т.е. в этой модели предполагается, что альфа-частица постоянно существует в
ядре.
Вероятность альфа-распада ![]() равна
произведению вероятности найти альфа-частицу на границе ядра f на вероятность ee
прохождения через потенциальный барьер D (прозрачность барьера)
равна
произведению вероятности найти альфа-частицу на границе ядра f на вероятность ee
прохождения через потенциальный барьер D (прозрачность барьера)
| λ = fD = ln2/T1/2. | (7) |
Можно отожествить f с числом соударений в единицу времени, которые испытывает альфа-частица о внутренние границы барьера, тогда
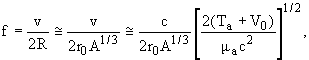 |
(8) |
где v, Ta, ![]() a
- скорость внутри ядра, кинетическая энергия и приведенная масса
альфа-частицы, V0 - ядерный потенциал. Подставив в выражение
(8) V0 = 35 МэВ, Ta = 5 МэВ, получим для ядер с A
a
- скорость внутри ядра, кинетическая энергия и приведенная масса
альфа-частицы, V0 - ядерный потенциал. Подставив в выражение
(8) V0 = 35 МэВ, Ta = 5 МэВ, получим для ядер с A ![]() 200, f
200, f ![]() 1021
с-1.
1021
с-1.
Hа рис.2 показана зависимость потенциальной энергии между
альфа-частицей и остаточным ядром от расстояния между их центрами. Кулоновский
потенциал обрезается на расстоянии R, которое приблизительно равно радиусу
остаточного ядра. Высота кулоновского барьера Bk определяется
соотношением
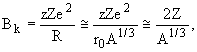 МэВ МэВ |
(9) |
Здесь Z и z - заряды (в единицах заряда электрона e) остаточного ядра и
альфа-частицы соответственно. Например для 238U Bk ![]() 30 МэВ.
30 МэВ.
Можно выделить три области.
|
|
(Аналогично влияние кулоновского барьера и в случае ядерной реакции, когда альфа-частица подлетает к ядру. Если ее энергия меньше высоты кулоновского барьера, она скорее всего рассеется кулоновским полем ядра, не проникнув в него и не вызвав ядерной реакции. Вероятность таких подбарьерных реакций очень мала.)
Квантово-механическое решение задачи о прохождении частицы через потенциальный барьер дает для вероятности прохождения (коэффициента прозрачности барьера) D
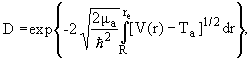 |
(10) |
где μα- приведенная масса, Tα - энергия α-частицы. В приближении Tα << Bk, где Bk - высота кулоновского барьера (предполагается, что барьер чисто кулоновский) описывается соотношением
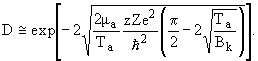 |
(11) |
Рассчитанные по формулам (7), (8) и (11) периоды полураспада правильно
передают важнейшую закономерность альфа-распада - сильную зависимость периода
полураспада T1/2 от энергии альфа-частиц Tα
(энергии альфа-распада Qα ![]() Tα ). При изменении периодов полураспада более чем на 20 порядков
отличия экспериментальных значений от расчетных всего 1-2 порядка. Конечно,
такие расхождения все же довольно велики. Где их источник и как надо
усовершенствовать теорию, чтобы эти расхождения с экспериментом уменьшить? Какие
факторы должны быть дополнительно учтены?
Tα ). При изменении периодов полураспада более чем на 20 порядков
отличия экспериментальных значений от расчетных всего 1-2 порядка. Конечно,
такие расхождения все же довольно велики. Где их источник и как надо
усовершенствовать теорию, чтобы эти расхождения с экспериментом уменьшить? Какие
факторы должны быть дополнительно учтены?
| V(r) = Vk (r) + Vц (r), | (12) |
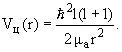 |
(13) |
Хотя высота центробежного барьера для тяжелых ядер при l = 8 составляет всего около 10% от высоты кулоновского барьера и центробежный потенциал спадает быстрее, чем кулоновский, эффект вполне ощутим и для больших l может приводить к подавлению альфа-распада более, чем на 2 порядка.
См. также
С.Г.Кадменский. Радиоактивность атомных ядер:
история, результаты, новейшие достижения
С.Д. Кургалин. Кластерный распад - новое явление
ядерной физики
С.Г.Кадменский. Кластеры в ядрах
17.11.15