В капельной модели ядро рассматривается как сферическая капля несжимаемой заряженной ядерной жидкости радиуса R = r0A1/3. То есть в энергии связи ядра учитываются объемная, поверхностная и кулоновская энергии. Дополнительно учитываются выходящие за рамки чисто капельных представлений энергия симметрии и энергия спаривания. В рамках этой модели можно получить полуэмпирическую формулу Вайцзеккера для энергии связи ядра.
Eсв(A,Z) = a1A - a2A2/3 - a3Z2/A1/3 - a4(A/2 - Z)2/A + a5A-3/4.
Первое слагаемое в энергии связи
ядра, подобного жидкой капле, пропорционально
массовому числу A и описывает примерное
постоянство удельной энергии связи ядер.
Второе слагаемое - поверхностная
энергия ядра уменьшает полную энергию связи, так
как нуклоны, находящиеся на поверхности имеют
меньше связей, чем частицы внутри ядра. Это
аналог поверхностного натяжения.
Третье слагаемое в энергии связи
обусловлено кулоновским взаимодействием
протонов. В капельной модели предполагается, что
электрический заряд протонов равномерно
распределен внутри сферы радиуса R = r0A1/3.
Четвертое слагаемое - энергия
симметрии ядра отражает тенденцию к
стабильности ядер с N = Z.
Пятое слагаемое - энергия спаривания
учитывает повышенную стабильность основных
состояний ядер с четным числом протонов и/или
нейтронов.
Входящие в формулу коэффициенты a1,
a2, a3, a4 и a5 оцениваются из
экспериментальных данных по знергиям связи ядер,
что дает
a1 = 15.75 МэВ; a2 = 17.8 МэВ; a3 = 0.711 МэВ; a4 = 23.7 МэВ;
 |
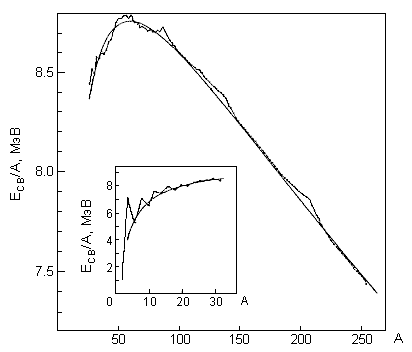Экспериментальные значения удельной энергии связи и расчет по формуле Вейцзеккера |
На рисунке показаны
экспериментальные значения удельной энергии
связи 
= Eсв/A
и расчет по формуле Вайцзеккера (плавная кривая).
Формула Вайцзеккера позволяет по
заданным значениям A и Z вычислять энергию связи
ядра с погрешностью ~10 МэВ. При 
100