Семинар 13

Теория электромагнитных взаимодействий – квантовая электродинамика (КЭД) является наиболее надежной и разработанной из физических теорий. Предсказания КЭД выполняются с высокой точностью. (Примером является рассмотренные в разделе 6 эффекты рождения пар кварков и мюонов при аннигиляции электронно-позитронных пар). Диаграммы Фейнмана являются не только иллюстрацией, но и основой методики расчета вероятности электромагнитных процессов. Электромагнитные процессы подчиняются почти всем законам сохранения (кроме закона сохранения изоспина ) Вероятности электромагнитных процессов, например распадов частиц с вылетом -квантов, меньше вероятностей распадов по сильным взаимодействиям. Сравним средние времена жизни частиц, распадающихся благодаря сильным и электромагитным взаимодействиям. Примером первого процесса является распад любого из -резонансов:

Δ⁺⁺ p + ⁺; Г = 120 МэВ.

Зная ширину резонансного пика Δ-частицы, можно оценить ее среднее время жизни:

Г = .

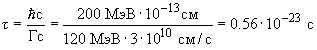Средние времена жизни частиц, распадающихся по электромагнитному каналу, гораздо больше. Например, среднее время жизни нейтрального пиона = 8.4·10^-17 с. Среднее время жизни нейтрального -гиперона, распадающегося на -гиперон и -квант, составляет = 7.4·10^-20 с. Заряженные пионы и заряженные -гипероны имеют средние времена жизни примерно на 9 порядков выше, чем их нейтральные партнеры по изоспиновым мультиплетам. Это различие во временах жизни связано с тем, что нейтральные пион и -гиперон распадаются благодаря электромагнитному взаимодействию, а заряженные – за счет слабого взаимодействия. Анализ диаграмм Фейнмана для электромагнитных взаимодействий адронов показывает, что при электромагнитных распадах не происходит превращения одного кварка в другой. Аннигиляция электрон-позитронной пары в два -кванта также (см. приложение к тексту лекции) не изменяет природу частицы в вершине (узле) диаграммы.
Взаимопревращение кварков друг в друга и одних лептонов в другие происходит за счет слабого взаимодействия.
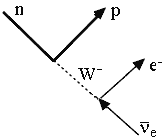
Слабое взаимодействие, ответственное за -распад ядер и частиц, рассматривалось в течение 50 лет как взаимодействие четырех фермионов. Действительно, в этих взаимодействиях может участвовать 4 фермиона, например

n p + e^- + _e; ... μ^- e^- + _e + ν_μ

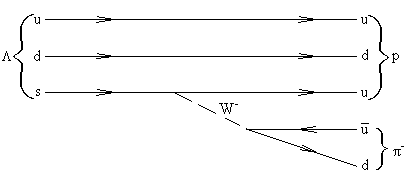
Однако существуют распады частиц, в которых не происходит вылета нейтрино (или антинейтрино), а превращаются друг в друга сильно взаимодействующие частицы – адроны. Например,

Λ p + π^-; K⁺ π⁺ + π⁰; Ξ^-Λ + π^-.

Эти процессы происходит за времена на 8 –9 порядков большие, чем электромагнитные распады, т.е. это распады по слабым взаимодействиям. Каков – на уровне диаграмм Фейнмана- механизм этих процессов? На этот вопрос физики-теоретики Вайнберг, Глэшоу и Салам нашли следующее решение: слабые взаимодействия являются, как и электромагнитные, обменными взаимодействиями. Но осуществляются они благодаря обмену тяжелыми промежуточными бозонами. В 1982-83 годах Карло Руббиа открыл промежуточные бозоны W⁺,W^- и Z⁰ на ускорителе SPS в европейском научном центре CERN. Массы покоя этих частиц оказались очень большими, больше 80 ГэВ. (Ответственный за электромагнитные взаимодействия -квант также является промежуточным бозоном, но, в отличие от W⁺, W^-, Z⁰ его масса покоя 0) Эксперимент подтвердил, таким образом, внутреннее единство процессов электромагнитного и слабого взаимодействия. Была создана единая теория электрослабых взаимодействий.

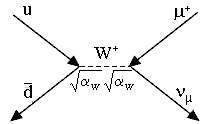
Задача 7.1. Оценить минимальные энергии пучков электронов и позитронов в коллайдере, при которых возможно рождение пар W⁺,W^-.

Реакции рождения промежуточных бозонов в e⁺e^- коллайдере

e⁺ + e^- W⁺+ W^-; e⁺ + e^- Z⁰ + Z⁰.

Поскольку массы покоя W⁺,W^-бозонов составляют по 80.41 ГэВ/с² ( или 80.41 ГэВ в “естественной системе”, принятой в физике высоких энергий), энергия каждого из сталкивающихся в коллайдере пучков e⁺,e^- должна составлять величину, не меньшую, чем масса покоя W, т.е. 80.41 ГэВ. Это пороговая энергия рождения пар W⁺, W^- в системе центра масс, при этой энергии сечение рождения этой пары близко к 0. Для получения заметного количества пар W⁺W^- энергия пучков e⁺, e^- должна быть выше 80.41 ГэВ.

Задача 7.2. Используя значения масс промежуточных бозонов, дать оценку радиуса слабых взаимодействий.

В слабых взаимодействиях обмен осуществляется путем рождения и поглощения массивных виртуальных частиц - промежуточных бозонов W⁺ ,W^-, Z⁰. Оценим, используя соотношение неопределенности, максимальное расстояние между фермионами, обменивающимися виртуальным промежуточным бозоном W. Для виртуальной частицы неопределенность в значении энергии равна ее энергии покоя: EM_wc². Энергия покоя W бозона около 80 ГэВ. Это приводит к очень малому радиусу слабых взаимодействий:

E R_W < ct c/M_w 0.2 ГэВ·Фм / 80 ГэВ 3·10^-16 см

Полученный результат объясняет тот факт, что созданная Ферми в в 30-х годах ХХ века теория слабых взаимодействий, как теория точечного взаимодействия 4-х фермионов, очень неплохо объясняла экспериментальные данные -распадов.
Нейтральный Z⁰ = Z бозон был обнаружен благодаря его распадам на кварк- антикварк, что приводило к регистрации струй адронов (Родившиеся кварки при разлете обрастают кварк-антикварковыми парами. В итоге формируются пучки адронов, летящие в направлениях вылета первичных кварков – струи (jet)). Другие каналы распада Z бозонов:

Z е⁺ + е^- и Z ⁺ + ^-.

Z бозоны ответственны за слабые процессы рассеяния части без изменения их зарядов в вершинах (т.н. нейтральные токи). Пример такого процесса – рассеяние нейтрино друг на друге.

7.2. Нейтрино и антинейтрино. Спиральность

Нейтрино, впервые обнаруженные в -распаде ядер, участвуют только в слабых взаимодействиях (и гравитационных, хотя измерить эти последние взаимодействия нейтрино пока не удается). Экспериментальное исследование реакций с нейтрино выявили следующие их характеристики:

1.Нейтрино и антинейтрино – разные частицы. Частица, излучаемая вместе с электроном в -распаде ядер – антинейтрино. Опыт показал, что антинейтрино не вызывают реакцию образования ядер аргона из ядер хлора, которая идет при участии нейтрино (например, нейтрино, которые излучаются Солнцем –опыт Дэвиса):

2.Нейтрино и антинейтрино бывают трех разных типов (flavor), соответствующих трем поколениям фундаментальных фермионов. Каждому из поколений лептонов, по современным представлениям, должно быть приписано свое квантовое число – лептонный заряд (L_e, L_μ, L_τ), которое сохраняется во всех взаимодействиях. Сохранение этого квантового числа объясняет отсутствие электромагнитных распадов мюонов μ е + γ. В слабом распаде лептонные заряды сохраняются.
Отличие мюонных и электронных нейтрино доказано прямыми экспериментами на пучках мюонных антинейтрино, которые возникают при распадах отрицательных пионов. Доказано, что при захвате этих нейтрино протонами возникают положительные мюоны и нейтроны, но не возникают позитроны и нейтроны:

_μ + p n + μ⁺;
_μ + p n + e⁺.

Вторая реакция не происходит!

3. Масса нейтрино очень мала даже по сравнению с массой электрона.

( По последним данным, масса электронного нейтрино меньше 5 эВ, измерение масс мюонных и тау-нейтрино еще более затруднительно, чем электронных нейтрино). Проблема массы нейтрино относится к важнейшим проблемам физики частиц и физики космоса.

4. Нейтрино обладает еще одной характеристикой – спиральностью h.

Спиральность равна величине проекции спина частицы на ее импульс, деленной на их модули.

(7.1)

Если нейтрино и антинейтрино - частицы ультрарелятивистские, т.е. их массы покоя равны 0, то для них должно выполняться правило

h() = +1; h() = -1.

(7.2)

То есть, если нейтрино и антинейтрино – частицы безмассовые, то нейтрино имеет точное значение этого квантового числа, равное –1, а антинейтрино +1. Чем ближе частица к пределу m = 0, тем более строго должно выполняться правило (7.2).

7.3. Превращения лептонов и кварков

    Правила построения диаграмм Фейнмана для электромагнитных и слабых процессов во многом одинаковы: 1) линии фермионов не прерываются; 2) связь фермионов осуществляется бозонами (-квантами для электромагнитных и W, Z бозонами для слабых взаимодействий); 3) каждой вершине соответствует константа взаимодействия; 4) все дискретные законы сохранения выполняются в каждой вершине; 5) закон сохранения энергии выполняется в целом для всего процесса, но нарушается в вершинах – соединяющие две вершины линии фермионов или бозонов соответствуют т.н. виртуальным частицам, для которых E² - P² m².
    Соответствующие обменам W или Z бозонам “слабые” вершины обладают еще одной особенностью, которой не имеют ни “сильные”, ни электромагнитные вершины – в этих вершинах может происходить превращение одного кварка в другой. Поэтому взаимопревращения адронов – результат слабых взаимодействий. Например, -распад нейтрона происходит благодаря превращению d-кварка в u-кварк при испускании виртуального W-бозона.
    Обмен заряженнымиW^- или W⁺ промежуточными бозонами связан с изменениями зарядов фермионов в вершине. “Треххвостка”, состоящая из двух фермионных линий, вершины и бозонной линии, называется “током”. Обмен заряженнымиW^- или W⁺ бозонами реализует заряженные токи. Обмен нейтральным Z –бозоном соответствует взаимодействию нейтральных токов.

Задача 7.3. Построить диаграмму Фейнмана распада нейтрона.

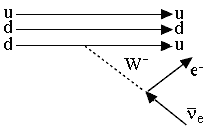
Как нейтрон, так и протон – барионы, состоящие из кварков. На рис.7.1 показаны два варианта изображения этого распада. При -распаде нейтрона происходит превращение d- кварка в u-кварк:

Рис.7.1

На этой диаграмме один из кварков, составляющих нейтрон, d-кварк, превращается благодаря испусканию виртуального W^- бозона в u-кварк протона. Превращение кварков (изменение “аромата” = ”flavor”) – свойство, присущее только слабым взаимодействиям. Именно благодаря слабым взаимодействиям тяжелые барионы и мезоны, содержащие кварки второго и третьего поколений, превращаются в более легкие барионы и мезоны.

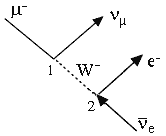
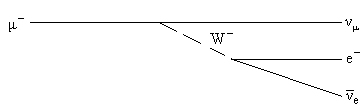
Задача 7.4. Изобразить ДФ распада мюона μ^-

e^- +

_e + ν_μ.

Рис.7.2.

Диаграммы Фейнмана для слабых взаимодействий строятся так же, как и ДФ для электромагнитных взаимодействий. В обоих случаях в вершинах диаграмм должны выполнятся все дискретные законы сохранения для данного типа взаимодействий, например, универсальный закон сохранения электрического заряда. Поскольку частица, которая осуществляет взаимодействие – виртуальная, законы сохранения энергии и импульса в вершинах временно нарушаются, но выполняются для процесса в целом.
При построении ДФ для этого процесса следует, как и в случае электромагнитных взаимодействий, учесть, что главный вклад вносит низшая по числу вершин диаграмма. В вершинах должны соблюдаться все дискретные законы сохранения (например, закон сохранения электрического заряда и лептонных зарядов). Поэтому ДФ распада мюона имеет вид оказанный на рис. 7.2. В вершинах соблюдаются законы сохранения лептонных зарядов L_μ и L_e. Отметим, что как в диаграмме распада нейтрона, так и распада мюона обменной частицей может быть как положительный, так и отрицательный W- бозон. Выбор его знака зависит от выбора направления линии бозона. ( Напомним, что в вершинах выполняется закон сохранения электрического заряда). Распад нейтрона относится к т.н. “полулептонным”, или лептон-адронным, распадам – в результате превращения адронов появляется пара лептонов. Распад мюона – лептонный, адроны в нем не участвуют. Существуют слабые процессы, в которых лептоны вообще не участвуют, например, адронные распады

Σ^-n + π^-, Ξ^-Λ +π^-.

Таким образом, слабые взаимодействия могут происходить с превращением кварков или лептонов одного аромата = ”flavor” в кварки и лептоны другого. Поэтому в слабых распадах не сохраняются ни изоспин, ни странность, ни шарм (charm). Нарушаются и законы сохранения topness и bottomness. Нарушения законов сохранения лептонных зарядов не наблюдалось.

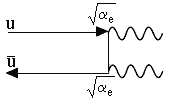
Задача 7.5. Изобразить диаграмму Фейнмана для распадов нейтрального и заряженного пионов. Оценить отношение констант слабого и электромагнитного взаимодействий, учитывая, что средние время жизни нейтрального и заряженных π-мезонов: τ(π⁰) = 8.4·10^-17 с;

(π⁺) =

(π^-) = 2.6·10^-8 с.


Рис.7.3

На рис. 7.3 показаны ДФ электромагнитного распада π⁰ мезона и слабого распада π⁺. Обе ДФ – второго порядка по константам взаимодействия. Как уже обсуждалось в Разделе 5, вероятности распадов пропорциональны квадратам констант взаимодействия . Отношение вероятностей распадов нейтрального и заряженного пионов обратно отношению их средних времен жизни. Отсюда

Константа слабого взаимодействия, согласно этой (весьма приближенной) оценке, α_w < 10^-6. Столь большое различие констант слабого и электромагнитного взаимодействий является следствием того факта, что электромагнитные взаимодействия реализуются обменом безмассовым фотоном, а промежуточные бозоны имеют большую массу. Отделение от величины константы множителя, связанного с массой обменного бозона, приводит для переопределенной константы слабого взаимодействия к величине

При росте энергий взаимодействия происходит сближение этих “констант” Таким образом, ЭСМ (электрослабая модель) получает еще одно подтверждение.
Необходимо подчеркнуть, что “константами” вершинные множители при расчете матричных элементов по методу диаграмм Фейнмана можно назвать лишь условно, поскольку значения этих величин зависят от энергии. В диапазоне энергий взаимодействия от 0 до 10 ГэВ изменение “констант” невелико.

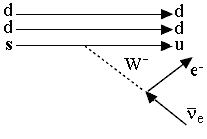
Задача 7.6. Построить диаграмму Фейнмана распада

-бариона. Какие законы сохранения нарушаются в этом распаде?

Рис. 7.4

Наиболее вероятный канал распада Λ-бариона Λ → p +π^-. Λ ~ (uds), p ~ (uud), π^- ~ (d). В распаде Λ-бариона не сохраняются странность и изоспин. Странность меняется на 1: ΔS = 1. Изменение изоспина равно |Δ| = 1/2.

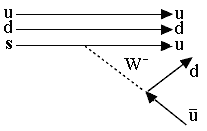
Задача 7.7. Построить диаграмму Фейнмана для наблюдаемого распада Σ^-→ n + e^- +

_e. Объяснить, почему не наблюдается распад Σ⁺→ n + e⁺ + ν_e.

Рис. 7.5

Кварковая структура первого распада (dds) → (ddu) + (лептоны), Кварковая структура второго распада (uus) → (ddu) + (лептоны). В распаде Σ^-→ n + e^- + _e происходит превращение s- кварка. Одной их возможных Д.Ф. является диаграмма слабого взаимодействия на рис.7.5. В результате распада виртуального W^- бозона рождается пара лептонов.
Для распада Σ⁺→ n + e⁺ + ν_e невозможно построить диаграмму второго порядка, поскольку Σ⁺ барион и нейтрон отличаются не одним, а двумя кварками: Σ⁺~ (uus), n ~ (udd). Процесс превращения двух кварков в два других не только на несколько порядков менее вероятен, но и должен сопровождаться рождением не одной, а двух пар лептонов.

7.4. Р-четность и С-четность. СР-четность

Как следует из раздела 7.3, слабые распады могут нарушать аддитивные законы сохранения I,s,c,b,t.

В слабых взаимодействиях нарушаются также мультипликативные законы сохранения пространственной (Р) и зарядовой (С) четностей.

Пространственная (Р) - четность.

Волновая функция частицы или системы частиц является функцией координат. Переход от выбранной системы координат к системе, соответствующей зеркальному отражению всех координатных осей, приводит к преобразованию волновой функции частицы или системы частиц. Оператор пространственного отражения

() = (-) = p();
() = p²() = (); p = +1.

(7.3)

Если гамильтониан системы коммутирует с оператором пространственного отражения, четность системы является “хорошим квантовым числом”, т.е. сохраняется.
Истинные и аксиальные вектора отличаются по четности:

()(-); ()(-);
()().

(7.4)

Напомним, что орбитальный момент является векторным произведением двух “истинных” векторов и поэтому он аксиальный вектор, как и спин частицы или системы частиц.
В сильных и электромагнитных взаимодействиях Р-четность сохраняется, но слабые взаимодействия нарушают пространственную симметрию и гамильтониан слабых взаимодействий не коммутирует с оператором Р-четности, то есть

|_weak,| - 0.

(7.5)

В таблицах адронов и кварков указывается одновременно спин и четность частицы в форме J^P. Например, для всех кварков J^P(q) =1/2⁺.
Р-четности всех антикварков равны (-1). (В таблицах указывается лишь знак квантового числа Р-четность).
Пространственная четность относится к мультипликативным квантовым характеристикам частиц или систем частиц. Четность системы частиц является произведением собственных четностей частиц и четности, соответствующей их орбитальному движению. Четность орбитального движения частицы с орбитальным моментом l равна P_l = (-1)^l.

Задача 7.8. Найти собственную четность протона и нейтрона.

Собственная четность нуклонов – систем (qqq) - равна +1, поскольку орбитальный момент кварков в нуклоне равен 0, и четность системы P(qqq) = P(q) P(q) P(q) = (+1)(+1)(+1) = +1.

Задача 7.9. Определить собственную четность π-мезона.

Все мезоны являются системами из кварка и антикварка. Наиболее легкие из мезонов - π-мезоны – это системы (q) с антипараллельными спинами и суммарным спином 0, поскольку орбитальный момент внутреннего движения кварка и антикварка в этих системах равен 0. Собственная четность любого π-мезона поэтому равна P(π) = P(q)P() = (+1)(-1) = -1.

Задача 7.10. Определить спины и Р-четности мезонов с орбитальным моментом кварк-антикварковой пары, равным 1. (По современной номенклатуре частиц - это f- мезоны)

Р-четность f мезонов равна P(f) = P(q)P()(-1)^l = (+1)(-1)(-1) = +1. Спин этих мезонов является векторной суммой собственных спинов кварка и антикварка и орбитального момента 1: = + + = 0, , . Эти значения спинов и четностей соответствуют f₀, f₁ и f₂ мезонам.

Р-четность и законы сохранения

Поскольку Р-четность сохраняется в сильных и электромагнитных взимодействиях, мультипликативный закон сохранения Р-четности применяется для того, чтобы определить значения квантовых чисел частиц в реакциях или найти правила отбора.

Задача 7.11. Проанализировать законы сохранения момента количества движения и Р-четности в реакции сильного ваимодействия π⁺ + p → Δ⁺⁺. Найти значения орбитального момента L системы пион-протон.

Спин Δ⁺⁺ резонанса 3/2. Закон сохранения момента количества движения в реакции рождения Δ-резонанса:

_π + _p + = 0 + + = .

Отсюда возможные значения L либо 1, либо 2.
Таким образом, из закона сохранения момента количества движения нельзя сделать однозначного вывода об орбитальном момента системы пион-нуклон в данной реакции. Но этот вывод можно сделать, если учесть еще один закон сохранения Р-четности: Р(π)Р(р)(-1)^L = (-1)(+1)(-1)^L = +1. Отсюда следует, что L = 1, т.е. реакция возбуждения Δ-резонанса при рассеянии пионов на нуклонах происходит при орбитальном моменте системы пион-нуклон, равном 1 (т.е. в р-канале)

Задача 7.12. Объяснить, почему не наблюдается распад η-мезона на два π-мезона.

Распад на два π-мезона по каналу сильного взаимодействия запрещен законом сохранения Р-четности, но распад на 3π-мезона идет:

η 3π⁰; P(η) = -1; P(3π⁰) = -1; P(2π⁰) = (-1)(-1) = +1.

C-Четность.
Операция зарядовой четности (С-четности) превращает частицу в античастицу.

|частица> |античастица>;
B - B; Q - Q.

(7.6)

Для истинно нейтральных частиц и систем волновая функция может быть собственной функцией оператора С-четности; эти частицы имеют определенное значение собственного значения этого оператора, т.е. имеют определенную С-четность.
Например, положительную (+) С-четность имеют нейтральные мезоны π и η. Отрицательной С-четностью обладает -квант. В электромагнитных взаимодействиях С-четность сохраняется. Это приводит к ряду “запретов” на распады частиц по каналу электромагнитных взаимодействий.

|> = _c|>; |> = -|>; _c() = -1.
⁰ + ; _c(π⁰) = +1; C(π⁰) = +1; C(3) = C()C()C() = -1.

Поэтому π не распадается на 3 !
Для систем частица-античастица _c = (-1)^l+s.
Система электрон-позитрон может быть либо в состоянии с s = 1 (ортопозитроний) либо в состоянии s = 0 (парапозитроний). Распады этих систем по электромагнитным взаимодействиям происходят по разному:

(e⁺ + e^-)_s=13, (_c) = -1; (e⁺ + e^-)_s=02, (_c) = +1.

С-четность сохраняется в сильных и электромагнитных взаимодействиях.

Несохранение Р- и С- четностей в слабых распадах можно показать, исследуя спиральность продуктов распада.

Задача 7.13. Объяснить, почему распад π⁺→ e⁺ + ν_e имеет вероятность, примерно в 10⁴ раза меньшую, чем распад π⁺→ μ⁺ + ν_μ.

		a
	P	(b)
	C	(c)
	CP	d
Рис. 7.6. Взаимная ориентация векторов импульсов (черные стрелки) и проекций спинов на направление движения (синие стрелки)

    Этот факт является следствием “правила спиральности” (7.2). Рассмотрим эти распады с точки зрения спиральностей возникающих лептонов в системе координат пиона: вследствие закона сохранения момента количества движения аксиальные вектора s имеют противоположные направления. Направления векторов импульса и момента количества движения противоположны для нейтрино (см.рис.7.6a). Если спиральность нейтрино “правильная” (-1), то для вылетающего в противоположном направлении мюона или электрона она равна тоже (-1 ) - т.е. “неправильная”. Для релятивистского электрона это приводит к подавлению вероятности этого распада по сравнению с мюонным распадом, поскольку мюон имеет примерно в 200 раз большую массу и, соответственно, правило спиральности для него может нарушаться.
    Покажем, что в распаде пиона, изображенном на рис.7.6, пространственная (или Р)-четность не сохраняется. Сохранение Р-четности равносильно утверждению, что при зеркальном отражении картина имеет тот же физический смысл.
    Р-отражение схемы (рис.7.6b) меняет направление вектора импульса, но не меняет направление вектора момента s . Если в схеме (a) антинейтрино имеет правильную спиральность, то в схеме (b), полученной в результате отражения ( т.е. Р-преобразования) – спиральность нейтрино неправильная ( h = +1), поскольку аксиальные вектора s не изменили своих направлений при Р-отражении.
    Итак, Р-преобразование картин распадов пионов приводит к неправильным спиральностям антинейтрино – что означает отсутствие симметрии по Р-четности в этих распадах. Иными словами, Р-четность в слабых распадах не сохраняется !
    Точно так же С-преобразование для указанных распадов (переход от положительных частиц к отрицательным без изменения направления векторов) дает для антинейтрино отрицательную – т.е. неправильную спиральность. Процесс распада не имеет С-инвариантности, С- четность не сохраняется. Но СР-четность в этом распаде сохраняется! Т.е. в результате последовательных Р и С отражений возникает “правильная” картина!
    Правило (7.3) запрещает распад нейтрального пиона на нейтрино и антинейтрино, который возможен по всем другим законам сохранения. Но распад нейтрального пиона на две ультрарелятивистские частицы неизбежно приводит к нарушению правила спиральностей для одной из них.
    Путем анализа спиральностей было показано, что в рассмотренных распадах по слабым взаимодействиям не сохраняются ни Р-, ни С-четность, но сохраняется СР (или, что то же самое РС) четность. Однако исследование распадов нейтральных К- мезонов , а в последние годы – нейтральных В⁰- мезонов, показало, что и эта четность не сохраняется, хотя степень нарушения очень мала. Рассмотрим СР- четности систем двух и трех пионов и нейтральных К- мезонов.

СР-ЧЕТНОСТЬ

|π⁺ + π^->_l=0 = +|π⁺ + π^->;
|π⁺ + π^- + π⁰> = -|π⁺ + π^- + π⁰>.

(7.8)

Нейтральные каоны не имеют определенной СР-четности, но суммы и разности их волновых функций имеют СР-четность .

|K⁰> = |K⁰>;

|K⁰> = -|K⁰>;

{|K⁰> + |K⁰>} = -{|K⁰> + |K⁰>}; |К⁰_L> =

{|K⁰> + |K⁰>};

{|K⁰> - |K⁰>} = +{|K⁰> - |K⁰>}; |К⁰_S> =

{|K⁰> - |K⁰>}.

(7.9)

Если СР сохраняется, распады частицы, волновая функция которой есть разность волновых функций нейтральных каона и антикаона (частица К⁰_S) должны происходить на 2 пиона, а частицы К⁰_L
(волновая функция которой составлена из сумма волновых функций каона и антикаона ) – на три пиона. Такие процессы, действительно, наблюдались. Причем первый распад идет много быстрее второго распада.
(τ(К⁰_S)10^-10 c; τ(К⁰_S)5·10^-8 c). Замечательной особенностью этих распадов является то, что из нейтрального К-мезона, в результате распада короткоживущей компоненты К_s, возникает суперпозиция нейтрального каона и антикаона, т.е. возникают т.н. осцилляции. Этот эффект экспериментально подтверждается! Если бы долгоживущий каон К_Lраспадался только на 3 пиона, проблемы нарушения СР четности не существовало бы. Но с малой вероятностью (меньше %) идет распада этого долгоживущего каона на 2 пиона, что и является нарушением СР четности.

CPT-теорема

    Доказано, что картина мира, полученная путем последовательного отражения пространственных осей (Р-отражение), заменой частиц на античастицы (С-отражение) и отражением оси времени (Т-отражение) приводит к картине, идентичной исходному состоянию. Иными словами, любой гамильтониан коммутирует с произведением операторов СРТ.
    Нарушение (хотя и слабое) СР инвариантности указывает поэтому на соответственное слабое нарушение Т- инвариантности уравнений движения.
    В настоящее время ведутся эксперименты по поиску прямых подтверждений нарушения Т-инвариантности.

Задание 5

Оценить среднее время жизни W и Z промежуточных бозонов.
Построить диаграмму Фейнмана для распада нейтрона.
Оценить верхний предел радиуса слабых взаимодействий из условия, что взаимодействие осуществляется за счет рождения и поглощения виртуального промежуточного W –бозона.
Рассчитать минимальную энергию пучков в коллайдере, необходимую для протекания реакции
e^- + e⁺ → W^- + W⁺.
Рассчитать кинетическую энергию электрона, рождающегося в распаде мюона. Построить диаграмму Фейнмана для этого распада.
Какие из перечисленных распадов возможны, a какие невозможны и почему
Σ⁰→ Λ + π⁰ ; Ω^-→ Λ + K^- ; Ω^-→ Λ + π^-, Ξ^-→ Λ + π ^-, π⁺→μ⁺ + ν_μ?
Почему не наблюдается распад 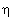-мезона на два пиона?
Почему не обнаружен распад μ⁺→ e⁺ + γ?
Сравнить средние времена жизни заряженных Σ-гиперонов и нейтрального Σ⁰-гиперона. Дать объяснение различию времен жизни.
Привести пример частиц, имеющих определенную С-четность.
Проверить закон сохранения С-четности в электромагнитных распадах нейтрального пи-мезона на 2γ и 3γ.
Привести примеры распадов частиц по каналам сильных, электромагнитных и слабых взаимодействий.
Проверить закон сохранения С-четности в электромагнитных распадах нейтрального пи-мезона на 2γ и 3γ.
Для любой реакции рождения странных частиц в р + р столкновениях написать наиболее вероятные пути распада продуктов вплоть до стабильных частиц.

7. Электромагнитные и слабые взаимодействия частиц. Распады

7.1. Электрослабые взаимодействия. Промежуточные бозоны

7.2. Нейтрино и антинейтрино. Спиральность

7.3. Превращения лептонов и кварков

7.4. Р-четность и С-четность. СР-четность

Пространственная (Р) - четность.

Р-четность и законы сохранения