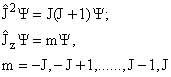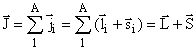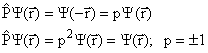Масса стабильных ядер меньше суммы масс входящих в ядро нуклонов.
Разность этих величин и определяет энергию связи ядра:
| E0(A,Z) = Zmp + (A-Z)mn - MN(A,Z) | (2.4) |
В (2.4) MN - масса ядра. В таблицах масс
приводятся, как правило, не массы ядер, а массы нейтральных атомов либо
величины, с ними связанные. Например, в “Практикуме по ядерной физике”
даны в приложении значения масс нейтральных атомов в единицах
1u = M(12C)/12 = 931.5 МэВ/с2
В приложении к сборнику “Субатомная физика” приведены
значения “избытков масс” 
= M - A, где М -
масса нейтрального атома в МэВ. Величина А представляет собой в данном случае
произведение числа нуклонов на значение единицы массы в МэВ. Таким образом,
величины приводятся в единицах МэВ, что очень удобно для
проведения расчетов.
Для примера вычислим величину энергии связи и удельной
энергии связи ядра 12С двумя способами: а) пользуясь таблицей масс в
единицах 1u и б) используя таблицу = M - A.
Прежде всего необходимо преобразовать формулу (2.4) , заменив
массы ядер M N на массы нейтральных атомов М:
M(A,Z) = MN(A,Z) + Zme |
(2.5) |
Формула (2.5) является приближенной - в ней опущены энергии связи электронов в атомах. Однако поскольку энергии связи нуклонов в ядре на 5 - 6 порядков превышают энергии связи электронов в атомах, это приближение не скажется на точности дальнейших расчетов энергий связи ядер. Прибавляя и вычитая Zme в (2.4), получим для энергии связи нуклонов в ядрах
Ebind = ZM(1H) + (A - Z)mn - M(A,Z) |
(2.6) |
Для ядра 12С по первому способу
Ebind = [6·1.007825 + 6·1.008665 -12.00000] · 931.5МэВ = 92.16 МэВ |
Для использования таблиц для = M-A преобразуем
Ebind = ZM(1H) + (A - Z)mn - M(A,Z) = Z |
(2.7) |
Для энергии связи 12С расчет этим способом проще:
Ebind = 6·7.289 МэВ + 6·8.071МэВ = 92.16 МэВ
Поэтому в дальнейших расчетах будет использоваться именно второй способ,
основанный на таблицах для = M-A.
Удельная энергия связи, т.е. энергия связи на один нуклон для ядра 12С
составляет
= Ebind/A = 92.16МэВ/12 = 7.68 МэВ
Распределение удельных энергий связи как функция числа
нуклонов А является наиболее важным для приложений экспериментальным результатом
физики ядра. Теоретическое объяснение этого распределения дает модель заряженной
жидкой капли и соответствующая этой модели формула Вайцзеккера.(См. далее
Модели ядер)
| Задача 2.4 Найти энергии отделения нейтрона и протона от ядра 12С. |
Энергия отделения нейтрона:
Bn = M(A - 1,Z) + mn - M(A,Z) =(A - 1,Z) + n -(A,Z)
Bn(12C) = 10.650 МэВ + 8.071 МэВ = 18.72 МэВ
Энергия отделения протона:
Bp = M(A-1,Z-1) + M(1H) - M(A,Z) =(A-1,Z-1) +(1H)-(A,Z)
Bp = (12C) = 8.668 МэВ + 7.289 МэВ = 15.96 МэВ
| Задача 2.5 Найти энергию отделения α-частицы от 12С. |
Ba = M(A-4,Z-2) + M(4He) - M(A,Z) =(A-4,Z-2) +(4He) -(A,Z)
Ba = (4.941 + 2.424) МэВ = 7.365 МэВ
Сравним результаты, полученные для удельной энергии связи ядра 12С
и энергий отделения от него нейтрона, протона и альфа частицы.
Энергия отделения одного нуклона от этого ядра оказалась более, чем вдвое выше
удельной энергии связи ! Энергия одновременного отделения кластера из 4 нуклонов
- α-частицы - меньше удельной энергии связи - т.е. средней энергии отделения
одного нуклона. Эти факты и аналогичные результаты для ряда других ядер стали
основой теоретической модели ядерных оболочек.
2.3. Спин ядра и моменты нуклонов
Основное и возбужденные состояния ядра и других квантовых систем характеризуется значениями моментов количества движения. Если ядро близко к сферическому, соответствующий ему гамильтониан коммутирует с оператором квадрата момента, что означает, что собственные значения этого оператора являются “хорошими квантовыми числами”, т.е. сохраняются. Как правило, ядерный гамильтониан коммутирует также с оператором проекции момента на одну из осей ( в качестве этой оси обычно выбирают ось z):
|
(2.8) |
Все перечисленные операторы действуют в пространстве волновых функций ядра 
:
|
(2.9) |
Спином ядра называется максимальное собственное
значение проекции момента на ось, т.е. величина J. Спины и моменты частиц и ядер
измеряются в единицах 
.
Спин нуклона, т.е.его момент в системе координат, связанной с ним, равен 1/2.
Частицы с полуцелыми значениями спинов называются фермионами.
Полный момент количества движения нуклона в
ядре складывается из его спина и орбитального момента относительно центра ядра:
|
(2.10) |
Спин ядра - результат сложения моментов нуклонов ядра :
|
(2.11) |
Сложение квантовых векторов происходит по следующим правилам. Если
вектор
то его величина
(т.е. максимальная проекция на выделенную ось в единицах ),
может принимать следующий ряд значений:
F = | |
(2.12) |
Подчеркнем еще раз, что результаты сложения квантовых векторов отличаются от
результатов сложения векторов в классической физике. Квантовый вектор
может пробегать лишь дискретный ряд значений (через единицу). Число разных
возможных значений вектора F зависит от того, какой из входящих в него векторов
больше. Число значений в наборе (2.12) равно 2Rmin + 1, где Rmin
- наименьший из векторов 
,
| Задача 2.5 Найти возможные значения полного момента j нейтрона с орбитальным моментом 3. Определить для каждого значения полного момента все возможные значения проекции на выделенную ось. |
Для j = 5/2 m j = -5/2,-3/2,-1/2,+1/2,+3/2,+5/2. (6 значений,
6=(5/2)+1)
Для j = 7/2 m j= -7/2,-5/2,-3/2,-1/2,+1/2,+3/2,+5/2,+7/2 (8
значений, 8 = 2(7/2)+1).
| Задача 2.6 Определить возможные значения спина ядра, состоящего из двух протонов и двух нейтронов в состояниях с орбитальными моментами, равными нулю. Считать все нуклоны находящимися в одном (низшем из возможных) энергетическом состоянии. |
Поскольку полные моменты всех нуклонов в данном случае
равны по 1/2, возможные значения суммы четырех векторов
Однако в физике реализуется только первое из этих значений, т.е. 0. Здесь (как и
в физике атома) проявляется действие принципа Паули. Согласно
принципу Паули, фермионы любой системы должны находиться в разных
квантовых состояниях.( Иными словами, фермионы не могут иметь
совпадающие наборы квантовых чисел).
В данном случае два нейтрона с одинаковой энергией и
одинаковыми (нулевыми) значениями орбитального момента должны иметь разные
значения проекции спина на выделенную ось, т.е. +1/2 и -1/2. Сумма спинов
нейтронов в этом случае равна 0. Эта же ситуация реализуется для двух протонов.
Поэтому суммарный момент такой четверки нуклонов - т.е. ядра 4 Не -
равен 0.
2.4. Четность ядерных состояний.
Волновая функция ядра является функцией координат составляющих его нуклонов. Переход от выбранной системы координат к системе, соответствующей зеркальному отражению всех координатных осей, приводит к преобразованию волновой функции системы. Оператор пространственного отражения
|
(2.13) |
Если гамильтониан системы коммутирует с оператором пространственного
отражения, четность системы является “хорошим квантовым числом”, т.е.
сохраняется. Для сильных и электромагнитных взаимодействий это выполняется,
поэтому (с точностью до малых добавок, связанных со слабыми взаимодействиями)
ядерные состояния имеют определенную четность. Принято указывать одновременно
спин и четность ядерного состояния в форме JP.
Например, в основном состоянии дейтрона (системы нейтрон-протон) JP = 1+.
Четность системы частиц является произведением собственных четностей частиц и
четности, соответствующей их орбитальному движению. Собственная четность
нуклонов +1.
Четность орбитального движения частицы с орбитальным моментом l
равна P = (-1)l.
Для системы нуклонов
P = Pl = (-1)∑l. |
(2.14) |
| Задача 2.7 Доказать, что орбитальный момент дейтрона может принимать только два значения: 0 либо 2. |
Четность дейтрона положительна, (-1)L = 1, следовательно L - четное число. Спин дейтрона равен 1. Суммарный спин двух нуклонов может принимать значения либо 0, либо 1.
Четному значению орбитального момента может соответствовать только суммарный спин 1. Поэтому значение орбитального момента есть результат вычитания (или сложения, что в случае векторов идентично) вектора полного момента и вектора спина:
