Составное ядро
Согласно модели составного ядра, ядерная реакция проходит в два этапа:
поглощение налетающей частицы ядром с образованием составного ядра и распад
составного ядра. Из-за сильного взаимодействия между нуклонами кинетическая
энергия налетающей частицы быстро перераспределяется между большим количеством
нуклонов промежуточной системы. В результате образуется квазиравновесная система
так называемое составное или компаунд-ядро. Так как энергия в составном ядре
статистически распределена между многими нуклонами, вероятность того, что один
из нуклонов будет иметь энергию, достаточную для вылета из ядра, мала, поэтому
время жизни составного ядра велико. Эмиссия из такой системы определяется
характеристиками составного ядра как целого и не зависит от способа его
образования. То есть в модели составного ядра сечение реакции с образованием
частицы b в конечном состоянии можно записать в виде
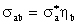 ,
(3.12) ,
(3.12)
где 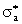 -
сечение образования составного ядра частицей a, ηb - вероятность
распада составного ядра по данному каналу b. Обычно ядро может распадаться
различными путями (по разным парциальным каналам): -
сечение образования составного ядра частицей a, ηb - вероятность
распада составного ядра по данному каналу b. Обычно ядро может распадаться
различными путями (по разным парциальным каналам):
γ-излучением, испуская нейтроны, протоны и т.д. Вероятность распада по данному
каналу определяется соотношением
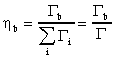 ,
(3.13) ,
(3.13)
где Гi - парциальные ширины распадов. Суммирование ведется по всем
открытым каналам, допускаемым законами сохранения. Окончательно можно записать
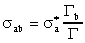 .
(3.14) .
(3.14)
Сечение образования составного ядра можно записать в виде
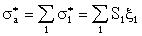 ,
(3.15) ,
(3.15)
где 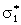 -
парциальное сечение поглощения налетающей частицы с данным орбитальным моментом
l, Sl - геометрическое сечение, равное доле всех частиц с орбитальным
моментом l, налетающих на ядро ξl - проницаемость, т.е. вероятность
проникновения частицы в ядро. В свою очередь проницаемость равна произведению
вероятностей прохождения кулоновского и центробежного барьеров на коэффициент
прохождения падающей дебройлевской волны через границу потенциала. Парциальное
геометрическое сечение Sl можно определить как площадь кольца со
средним радиусом равным прицельному параметру -
парциальное сечение поглощения налетающей частицы с данным орбитальным моментом
l, Sl - геометрическое сечение, равное доле всех частиц с орбитальным
моментом l, налетающих на ядро ξl - проницаемость, т.е. вероятность
проникновения частицы в ядро. В свою очередь проницаемость равна произведению
вероятностей прохождения кулоновского и центробежного барьеров на коэффициент
прохождения падающей дебройлевской волны через границу потенциала. Парциальное
геометрическое сечение Sl можно определить как площадь кольца со
средним радиусом равным прицельному параметру 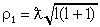
Sl = (2l + 1)π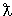 2. (3.16) 2. (3.16)
Таким образом сечение образования составного ядра можно записать в виде
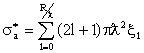 .
(3.17) .
(3.17)
Так как ядерные силы короткодействующие, то они влияют на частицы с
прицельными параметрами 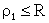 , в связи с этим
суммирование ведется от 0 до lmax ≈ R/ , в связи с этим
суммирование ведется от 0 до lmax ≈ R/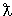 . .
Сечение ограничено сверху геометрическим сечением, когда ξl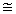 1 1
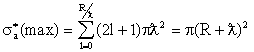 .
(3.18) .
(3.18)
Для медленных нейтронов для которых существенна только s-волна (l = 0),
расчет проницаемости сводится только к учету вероятности прохождения волны через
границу ядерного потенциала и определяется соотношением
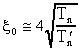 ,
(3.19) ,
(3.19)
где Tn и 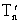 -
кинетические энергии нейтрона вне и внутри ядра. Для медленных нейтронов -
кинетические энергии нейтрона вне и внутри ядра. Для медленных нейтронов 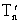 практически равна глубине ядерного потенциала т.е. ~ 30 МэВ.
практически равна глубине ядерного потенциала т.е. ~ 30 МэВ.
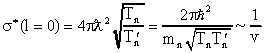 ,
(3.20) ,
(3.20)
где v - скорость нейтрона.
При энергиях частиц, при которых энергия возбуждения составного ядра близка к
резонансной, сечение реакции описывается формулой Брейта-Вигнера:
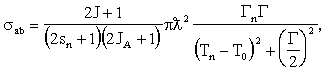 (3.21)
(3.21)
где sn, JA, и J - спины нейтрона, ядра и составного
ядра соответственно, Гn, Г - нейтронная и полная ширины, Tn,
T0 - энергия нейтрона и энергия резонанса.
При малых энергиях нейтронов возможны только процессы (n, n) (n,γ),
так что Г = Гn + Гγ,
причем Гn~v,
Гγ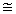 const.
Таким образом при достаточно малых энергиях Гn<<Гγ (для ядер с A >
100 это условие выполяется для энергии нейтронов вплоть до сотен кэВ) и . const.
Таким образом при достаточно малых энергиях Гn<<Гγ (для ядер с A >
100 это условие выполяется для энергии нейтронов вплоть до сотен кэВ) и .
Угловые распределения вылетающих частиц в реакциях идущих через составное ядро
симметричны относительно 900 в системе центра масс. В области
перекрывающихся резонансов составного ядра* они имеют максимумы при 00
и 1800 и минимум при 900, причем этот минимум тем глубже,
чем выше угловой момент составного ядра.

|
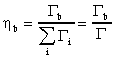 ,
(3.13)
,
(3.13) 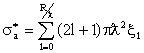 .
(3.17)
.
(3.17) 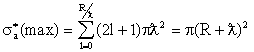 .
(3.18)
.
(3.18) 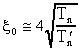 ,
(3.19)
,
(3.19) 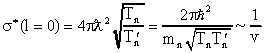 ,
(3.20)
,
(3.20) 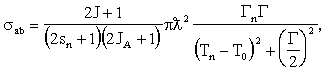 (3.21)
(3.21)