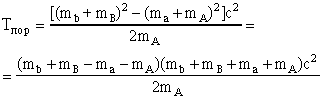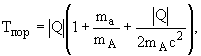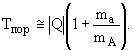Вычислим величину порога эндотермической реакции. Соотношения
|
(cl.5) |
| (cl.6) |
справедливы для любой инерциальной системы координат. В лабораторной системе координат, когда налетающей частицей является частица a, а частица A до столкновения покоится имеем
|
|
(cl.10) |
|
|
(cl.11) |
В системе центра инерции
|
|
(cl.12) |
|
|
(cl.13) |
В соотношениях (cl.10, cl.12) E - полная энергия (E = T + mc2, где T - кинетическая энергия). Кинетическая энергия налетающей частицы в л.с. равна пороговой, когда в с.ц.и. кинетические энергии продуктов реакции равны 0, т.е.
|
|
(cl.14) |
|
|
(cl.15) |
Выпишем релятивистский инвариант в с.ц.и.
|
|
(cl.16) |
В лабораторной системе, учитывая, что Ea = mac2 + Tпор,
|
(cl.17) |
Подставив в (cl.17) вместо импульса его выражение через кинетическую энергию
|
|
(cl.18) |
получим
|
|
(cl.19) |
Учитывая, что
|
|
(cl.20) |
получим
|
|
(1.21a) |
или
|
|
(cl.21б) |
где Q -энергия реакции, ma - масса
налетающей частицы, mA - масса ядра мишени.
В нерелятивистском приближении (Q<< 2mAc2)
|
|
(cl.21в) |
Отметим, что соотношения (cl.21бв) справедливы и для реакций с любым количеством частиц в конечном состоянии.
Пример. Рассмотрим двe реакции взаимодействия легкой частицы, например протона с более тяжелым ядром. В первом случае налетающей частицей является протон, во втором - ядро. Тогда согласно (cl.21в) Отношение порогов этих реакций будет равно отношению масс - Tпор2/Tпор1 = mядра/mp. Во втором случае заметно большая доля кинетической энергии бесполезно расходуется на движение центра инерции системы.