4. Двойной бета-распад
В природе существует большое число стабильных четно-четных
ядер-изобар с
зарядом отличающимся на две единицы (A,Z)
и (A,Z±2).
Существование таких ядер обусловлено двумя причинами.
- Силы спаривания между двумя протонами или двумя нейтронами в ядре
приводят к увеличению энергии связи четно-четного ядра по сравнению с
четно-нечетным ядром (A,Z±1).
- Часто промежуточное ядро-изобар (A,Z±1) обладает большей массой, чем
ядра (A,Z) и (A,Z±2), поэтому превращение ядра (A,Z) в более лёгкое ядро (A,Z±2)
не может происходить путём двух последовательных β-распадов
(рис. 4.1)
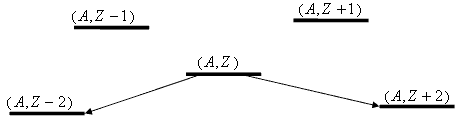
Рис. 4.1. Энергетическая диаграмма, поясняющая процесс
двойного
β-распада.
В этих случаях превращение ядра (A,Z)
в ядро-изобар (A,Z±2)
может происходить с одновременным испусканием двух электронов или двух
позитронов. Впервые на это обратила внимание М. Гепперт-Майер в 1935 г.
[Goeppert-Mayer, M., 1935, Phys. Rev. 48, 512].
При двойном β-распаде атомное ядро (A,Z)
испускает два электрона и два антинейтрино или два позитрона и два нейтрино,
превращаясь в ядро с тем же массовым числом А (ядро-изобару) и электрическим
зарядом больше или меньше на две единицы.
(A,Z) → (A,Z+2) + 2e- + 2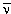 e, e, |
(4.1) |
| A,Z) → (A,Z-2) + 2e+ + 2νe, |
(4.2) |
К процессам двойного β-распада
относятся также процессы типа е-захвата на ядре (A,Z)
с последующим образованием в конечном состоянии позитрона и двух нейтрино
| e- + (A,Z) → (A,Z-2) + e+
+ 2νe, |
(4.3) |
а также процесс двойного электронного захвата
| 2e- + (A,Z) → (A,Z-2) + 2νe. |
(4.4) |
В случае (4.1) двойной β--распад
сопровождается увеличением заряда ядра на две единицы (A,Z) → (A,Z+2)
и излучением двух электронов и двух электронных антинейтрино 2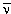 e.
В других видах двойного β-распад
(4.2, 4.3, 4.4) заряд ядра уменьшается на две единицы (A,Z) → (A,Z-2)
и сопровождается испусканием двух электронных нейтрино 2νe.
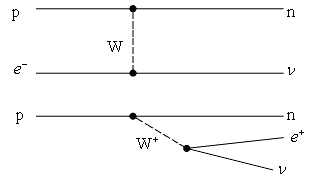
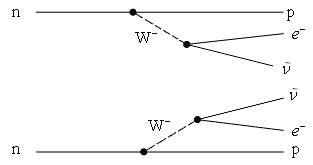
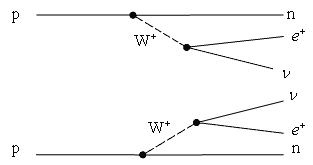
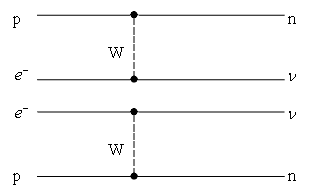
Диаграмма Фейнмана двойного β-распада
показана на рис. 4.2. e.
В других видах двойного β-распад
(4.2, 4.3, 4.4) заряд ядра уменьшается на две единицы (A,Z) → (A,Z-2)
и сопровождается испусканием двух электронных нейтрино 2νe.
Диаграмма Фейнмана двойного β-распада
показана на рис. 4.2.
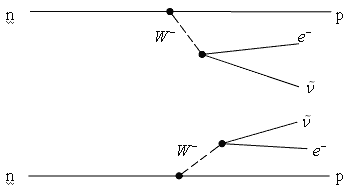
Рис. 4.2. Диаграмма Фейнмана двойного β--распада.
Обычно процессы двойного β-распада
сопровождаются испусканием двух нейтрино 2νe
или двух антинейтрино 2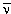 e,
что следует из закона сохранения лептонного числа Le. e,
что следует из закона сохранения лептонного числа Le.
Для того, чтобы наблюдался процесс двойного β-распада,
необходимо, чтобы масса начального ядра (A,Z)
была больше массы ядра (A,Z+2)
или
(A,Z-2),
образующегося в результате двойного β-распада.
Двойной
β-распад
очень редкий процесс. Для того, чтобы его наблюдать необходимо, чтобы цепочка
двух последовательных β-распадов
(A,Z) → (A,Z+1) + e- +
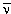 e→ (A,Z+2) + 2e-
+ 2 e→ (A,Z+2) + 2e-
+ 2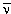 e, e,
(A,Z) → (A,Z-1) + e+ + νe→ (A,Z-2) + 2e+ + 2νe,
была запрещена по энергии или сильно подавлена законом сохранения полного
момента количества движения. Двойной β--распад наблюдается
у лёгких изотопов химического элемента, в то время как для
тяжелых изотопов двойной β--распад не наблюдается.
В качестве примера можно привести два изотопа кадмия
108Cd и 116Cd. В то время, как для изотопа 116Cd
наблюдается двойной β--распад,
в изотопе 108Cd возможный двойной β--распад до сих пор не наблюдался.
Энергетическое условие 2β--распада
Мяд(A,Z) > Mяд(A,Z+2) + 2me
или, переходя к массам атомов,
Мат(A,Z) > Mат(A,Z+2).
Энергия, выделяющаяся при 2β--распаде
Q(2β-) = [Мат(A,Z) − Mат(A,Z+2)]c2.
Энергетическое условие 2β+-распада
Мяд(A,Z) > Mяд(A,Z-2) + 2me,
Мат(A,Z) > Mат(A,Z-2) + 4me.
Энергия, выделяющаяся при 2β+-распаде
Q(2β+) = [Мат(A,Z) − Mат(A,Z+2) − 4me]c2.
Энергетическое условие 2e-захвата
Мяд(A,Z) + 2me > Mяд(A,Z-2),
Мат(A,Z) > Mат(A,Z-2).
Энергия, выделяющаяся при 2e-захвате
Q(2e) = [Мат(A,Z) − Mат(A,Z+2)]c2 − 2ε,
где ε − энергия связи орбитального электрона.
Энергетическое условие е-захвата
e- + (A,Z) → (A,Z-2) + e+ + 2νe
Мяд(A,Z) > Mяд(A,Z-2),
Мат(A,Z) > Mат(A,Z-2) + 2me.
Энергия, выделяющаяся в е-захвате
e- + (A,Z) → (A,Z-2) + e+ + 2νe
Q(e-,e+2ν) = [Мат(A,Z) − Mат(A,Z-2) −
2me]c2 − ε.
Двойной
β-распад
может происходить не только на основное, но и в возбужденные состояния конечного
ядра. В этом случае он сопровождается излучением нескольких γ-квантов
и (или) конверсионных электронов.
Изотопы, для которых возможен двойной β--распад
приведены в таблице 4.1.
Таблица 4.1.
Четно-четные изотопы, для которых возможен двойной β--распад
|
№ |
Распад
(A,Z)→(A,Z+2) |
A
|
Z
|
Энергия
β--распада |
Энергия
β-перехода
(A,Z)→(A,Z+1), кэВ |
|
1 |
Ca → Ti |
46
|
20
|
984.5 ± 5.1 |
–1382.6 ± 3.7 |
|
2
|
Ca → Ti |
48
|
20
|
4271.7 ± 5.4
|
+281 ± 6 |
|
3
|
Zn → Ge |
70
|
30
|
1001.5 ± 5.2
|
–654.8 ± 1.6 |
|
4
|
Ge → Se |
76
|
32
|
2045.7 ± 5
|
–922.9 ± 2.7 |
|
5
|
Se → Kr |
80
|
34
|
135.7 ± 14.5
|
–1870.3 ± 2 |
|
6
|
Se → Kr |
82
|
34
|
3005 ± 16
|
–88 ± 12 |
|
7
|
Kr → Sr |
86
|
36
|
1249.1 ± 7.8
|
–526 ± 5 |
|
8
|
Zr → Mo |
94
|
40
|
1148.4 ±6.5
|
–896.8 ± 2.6 |
|
9
|
Zr → Mo |
96
|
40
|
3350.2 ± 6.1
|
+163.0 ± 5 |
|
10
|
Mo → Ru |
98
|
42
|
110.6 ± 8.4
|
–1682 ±5 |
|
11
|
Mo → Ru |
100
|
42
|
3032.6 ± 8.6
|
–170 ± 6 |
|
12 |
Ru → Pd |
104
|
44
|
1301 ± 11
|
–1147 ± 7 |
|
13
|
Pd → Cd |
110
|
46
|
2014 ± 24
|
–879 ± 20 |
|
14
|
Cd → Sn |
114
|
48
|
540.4 ±7.3
|
–1444 ± 5 |
|
15
|
Cd → Sn |
116
|
48
|
2808.5 ±7.3
|
–464 ± 8 |
|
16
|
Sn → Te |
122
|
50
|
358 ± 8
|
–1622.7 ± 3.6 |
|
17
|
Sn → Te |
124
|
50
|
2278б3 ± 8б8 |
–627 ± 5 |
|
18 |
Te → Xe |
128
|
52
|
868.9 ± 5.5
|
–1258 ± 5 |
|
19
|
Te → Xe |
130
|
52
|
2533.1 ± 6.6
|
–451 ± 11 |
|
20
|
Xe → Ba |
134
|
54
|
843 ± 15
|
–1215 ± 11 |
|
21
|
Xe → Ba |
136
|
54
|
2481 ± 15
|
–67 ± 11 |
|
22
|
Ce → Nd |
142
|
58
|
1414 ± 11
|
–745.1 ± 3.5 |
|
23
|
Nd → Sm |
148
|
60
|
1928 ± 10
|
–536 ± 9 |
|
24
|
Nd → Sm |
150
|
60
|
3367 ± 11
|
–130 ± 80 |
|
25
|
Sm → Gd |
154
|
62
|
1250 ± 10
|
–728 ± 5 |
|
26
|
Gd → Dy |
160
|
64
|
1731 ± 11
|
–102.3 ± 1.4 |
|
27
|
Yb → Hf |
176
|
70
|
1077 ± 12
|
–109.6 ± 21 |
|
28
|
W → Os |
186
|
74
|
489 ± 14
|
–587.8 ± 2.6 |
|
29
|
Pt → Hg |
198
|
78
|
1043 ± 26
|
–330 ± 19 |
|
30
|
Hg → Pb |
204
|
80
|
414 ± 12
|
–349 ± 5 |
|
31
|
U → Pu
|
238
|
92
|
1146.2 ± 4.6
|
–145.6 ± 1.3 |
Изотопы, для которых возможен двойной β--распад
приведены в таблице 4.2.
Таблица 4.2.
Четно-четные изотопы, для которых возможен двойной β+-распад
|
№
|
Распад
(A,Z)→(A,Z–2) |
A
|
Z
|
Энергия
2β+-распада
|
Энергия
β-перехода
(A,Z)→(A,Z–1), кэВ
|
|
1
|
Ar → Se
|
36
|
18
|
434.58 ± 1.78
|
–709.55 ± 0.30
|
|
2
|
Ca → Ar
|
40
|
20
|
193.4 ± 1.5
|
–1311.6 ± 0.5
|
|
3
|
Cr → Ti
|
50
|
24
|
1174.1 ± 4
|
–1038.7 ± 1.4
|
|
4
|
Fe → Cr
|
54
|
26
|
679.9 ± 3
|
–697.1 ± 1.7
|
|
5
|
Ni → Fe
|
58
|
28
|
1927.5 ± 3.1
|
–380.2 ± 1.2
|
|
6
|
Zn → Ni
|
64
|
30
|
1096.7 ± 3.5
|
–578.2 ± 1.5
|
|
7
|
Se → Ge
|
74
|
34
|
1209.4 ± 4.5
|
–1353.1 ± 2.6
|
|
8
|
Sr → Kr
|
84
|
38
|
1790.3 ± 7.6
|
–890.0 ± 3.5
|
|
9
|
Mo → Kr
|
92
|
42
|
1649.1 ± 6.8
|
–359 ± 4
|
|
10
|
Ru → Mo
|
96
|
44
|
2719.9 ± 11.4
|
–254 ± 10
|
|
11
|
Pd → Ru
|
102
|
46
|
1175.5 ± 11.9
|
–1148 ± 6
|
|
12
|
Cd → Pd
|
106
|
48
|
2782 ± 11
|
–202 ± 9
|
|
13
|
Cd → Pd
|
108
|
48
|
272 ± 11
|
–1649 ± 8
|
|
14
|
Sn → Cd
|
112
|
50
|
1919.9 ± 9.4
|
–658 ± 6
|
|
15
|
Te → Sn
|
120
|
52
|
1697.8 ± 24.5
|
–983 ± 22
|
|
16
|
Xe → Te
|
124
|
54
|
3068.3 ± 143.8
|
–90 ± 140
|
|
17
|
Xe → Te
|
126
|
54
|
904 ± 12
|
–1251 ± 5
|
|
18
|
Ba → Xe
|
130
|
56
|
2578.1 ± 13.6
|
–440.9 ± 3.9
|
|
19
|
Ba → Xe
|
132
|
56
|
833 ± 15
|
–1279 ± 24
|
|
20
|
Ce → Ba
|
138
|
58
|
708 ± 20
|
–1041 ± 12
|
|
21
|
Gd → Sm
|
152
|
64
|
58 ± 14
|
–1819.2 ± 3.3
|
|
22
|
Dy → Gd
|
156
|
66
|
2009 ± 14
|
–428 ± 8
|
|
23
|
Dy → Gd
|
158
|
66
|
281 ± 11
|
–935.4 ± 3.6
|
|
24
|
Er → Dy
|
162
|
68
|
1846 ± 12
|
–288 ± 5
|
|
25
|
Er → Dy
|
164
|
68
|
27 ± 12
|
–1002 ± 4
|
|
26
|
Yb → Er
|
168
|
70
|
1420 ± 13
|
–259 ± 4
|
|
27
|
Yb → Er
|
170
|
60
|
655 ± 12
|
–967.9 ± 0.9
|
|
28
|
Hf → Yb
|
174
|
72
|
1110 ± 14
|
–268.0 ± 6
|
|
29
|
Os → W
|
184
|
76
|
1454 ± 14
|
–42 ± 6
|
|
30
|
Pt → Os
|
192
|
78
|
408 ± 14
|
–1456.9 ± 3.8
|
|
31
|
Hg → Pt
|
196
|
80
|
806 ± 16
|
–684 ± 3.9
|
Двойной
β-распад
является самым редким типом радиоактивного распада. Во всех случаях, в которых
достоверно установлен этот тип распада, периоды полураспада больше 1018
лет, что на несколько порядков превышает время существования Вселенной.
Основная трудность, с которой сталкиваются при проведении экспериментов по
изучению двойного
β-распада,
обусловлена малой вероятностью события, необходимостью проведения длительных
экспериментов, максимального снижения фоновых событий и тщательного анализа
результатов эксперимента. Поэтому для поиска двойного бета-распада
используются различные методики, которые можно разделить на три большие группы:
- геохимические,
- радиохимические,
- прямое наблюдение.
Использование геохимических методов обусловлено возможностью увеличения
продолжительности наблюдений до времен ~109
лет. В этих экспериментах анализируются древние минералы, имеющие возраст
несколько миллиардов лет и выделяются продукты
2β-распада.
Двойной
β-распад 130Te впервые был обнаружен в результате геохимического анализа
теллурида висмута Bi2Te3
шведских рудных месторождений возраст которых составляет (1.5±0.5)
млрд. лет. В результате термической обработки был исследован изотопный состав
Xe, образующегося в результате распада Te. Оказалось, что изотопный состав Xe,
извлеченного из руды сильно отличается от изотопного состава атмосферного Xe. В
результате тщательного анализа фоновых условий было показано, что 130Xe
образуется в
2β--распаде
130Te → 130Xe + 2e- + 2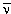 e e
и оценен период полураспада T1/2(2β2ν) ≈ 1021
лет. Позже этот результат был подтвержден в прямых экспериментах. Измеренный
период двойного β-распада 130Te составил
(2.7±0.1)·1021лет.
Радиохимическим методом был измерен период двойного
β-распада
изотопа 238U [Turkevich A.L., Economou T.E., Cowan A. Phys. Rev.
Lett. 1991, V67, 3211]. Для этого из нескольких тонн урана 238U был
выделен продукт двойного β--распада
238Pu
238U → 238Pu + 2e- + 2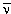 e e
и получен период полураспада 238U
относительно двойного β-распада
|