Распределение заряда и массы в атомных ядрах исследуется в экспериментах по упругому рассеянию на ядрах альфа-частиц (исторически это первые эксперименты Резерфорда), электронов и протонов. Выяснилось, что как плотность распределения заряда, так и плотность распределения массы ядра приближенно выражаются распределением Ферми:
  |
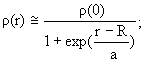(1.5) |
Величину R называют радиусом ядра. Отметим, что поскольку распределение плотности заряда и массы близки, но не совпадают друг с другом, отличаются также и зарядовый и массовый радиусы. В приближенных расчетах можно считать эти величины совпадающими и полагать, что радиус ядра
R r0A1/3. |
(1.6) |
Это одновременно означает независимость средней плотности ядра от массового числа. Действительно, оценим плотность ядра с числом нуклонов А:
 . |
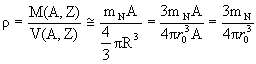(1.7) |
 Рис.1.1. Радиус распределения заряда в некоторых ядрах по данным (e,e) реакций. |
Полученные результаты для плотности и радиуса эквивалентны утверждению о полной несжимаемости ядерной материи. В большинстве приближенных расчетов это утверждение можно использовать, однако отклонение от него хорошо видно на примере распределения среднеквадратичного радиуса распределения заряда для разных ядер. На рис.1.1 показаны результаты исследований среднеквадратичного зарядового радиуса для некоторых ядер, полученные в экспериментах по неупругому рассеянию электронов на ядрах. Следует обратить внимание на отклонение величины зарядового радиуса от (1.6). Например, зарядовый радиус ядра 48Са меньше, чем зарядовый радиус ядра 40Са. Для изотопов титана рост А ведет к уменьшению зарядового радиуса. Эти эффекты нашли качественное объяснение в модели ядерных оболочек.
Энергии связи и массы ядер
Масса стабильных ядер меньше суммы масс входящих в ядро нуклонов, - разность этих величин и определяет энергию связи ядра Eсв (binding energy ):
| Eсв(A,Z) = Zmp + (A - Z)mn - MN(A,Z). | (1.8) |
В (1.9) MN - масса ядра. В таблицах масс
приводятся не массы ядер, а массы нейтральных
атомов, либо величины, с ними связанные. В
приложении к сборнику “Субатомная физика”
приведены значения “избытков масс”
= M - A, где М – масса
нейтрального атома в МэВ. (Избытки масс и не
только можно найти в базе данных "Параметры
основных состояний атомных ядер").
Величина А представляет собой в данном случае
произведение числа нуклонов на значение единицы
массы в МэВ. Таким образом, величины приводятся в единицах
МэВ, что очень удобно для проведения расчетов.
| M(A,Z) = MN(A,Z) + Zme; (A,Z) = M(A,Z) - A. |
(1.9) |
Формула (1.8) является приближенной – в ней опущены энергии связи электронов в атомах. Однако поскольку энергии связи нуклонов в ядре на 5 – 6 порядков превышают энергии связи электронов в атомах, это приближение не скажется на точности дальнейших расчетов энергий связи ядер.
| Eсв(A,Z) = ZM(1H) + (A -
Z)mn - M(A,Z) = Z(1H)
+ (A - Z)n - (A,Z) |
(1.10) |
 Рис. 1.2. Удельная энергия связи на нуклон как функция числа нуклонов А. |
Распределение удельных энергий
связи 
= Eсв/A как
функция числа нуклонов А является наиболее
важным для приложений экспериментальным
результатом физики ядра (Рис.1.2) .
Экспериментально установленное
распределение удельных энергий связи ядер по
значениям чисел нуклонов в ядре А имеет
следующие характерные черты:
В широкой области ядер удельная
энергия связи очень
слабо зависит от А; для ядер с малыми А удельная
энергия имеет “спад”.
Для тяжелых ядер средняя удельная
энергия связи меньше, чем для средних, причем с
ростом А наблюдается снижение ее величины.
Для ядер с Z = N удельная энергия
выше, чем для других ядер с тем же значением А.
Четно-четные (по Z и N) ядра имеют в
среднем большие значения , чем нечетно-четные, а нечетно-нечетные –
меньшие.
Теоретическое объяснение этого
распределения дает модель
заряженной жидкой капли и соответствующая
этой модели формула Вайцзеккера.
Первая из перечисленных (и главная)
особенность распределения удельных энергий
связи ядер – следствие насыщения
ядерных сил. Вторая связана с тем, что связи
нуклонов, находящихся на поверхности ядра, с
другими нуклонами ядра не полностью насыщены.
Чем больший процент нуклонов находится на
поверхности ядра, тем больше “убыль” энергии
насыщения. (Этими особенностями ядерные силы
оказываются подобны силам, действующим между
молекулами жидкости). Третья особенность
распределения удельной энергии связи
объясняется тем, что протоны ядер участвуют не
только в сильном (ядерном), но и в
электромагнитном взаимодействии. Чем больше
протонов, тем выше энергия кулоновского
отталкивания. Четвертая и пятая особенности
распределения – следствия оболочечной
структуры ядра и симметрий, связанных с
реализацией в ядре принципа Паули.
Учет всех перечисленных свойств
приводит к полуэмпирической формуле
Вайцзеккера, или модели заряженной жидкой капли:
| Eсв = a1A - a2A2/3 - a3Z2/A1/3 - a4(A - 2Z)2/A + a5A-1/2. | (1.11) |
Коэффициенты в (1.11) подбираются из условий наилучшего совпадения кривой модельного распределения с экспериментальными данными. Поскольку такая процедура может быть проведена по-разному, существует несколько наборов коэффициентов формулы Вайцзеккера. В работе [P. Roy Chowdhury, D.N. Basu. Nuclear Matter Properties with the Revaluated Coefficients of Liquid Drop Model. Acta Phys. Polonica B, vol.37 (2006) No 6, pp. 1833-1846] в результате подгонки (1.11) к экспериментально измеренным значениям атомных масс были получены следующие коэффициенты:
a1 = 15,409 МэВ; a2 = 16,873 МэВ; a3 = 0,695
МэВ; a4 = 22,435 МэВ;
Несложно оценить значение
зарядового числа Z, при котором ядра становятся
нестабильными по отношению к спонтанному
распаду.
Спонтанный распад ядра возникает в
случае, если кулоновское расталкивание протонов
ядра начинает преобладать над стягивающими ядро
ядерными силами. Оценка ядерных параметров, при
которых наступает такая ситуация, может быть
проведена из рассмотрения изменений в
поверхностной и кулоновской энергиях при
деформации ядра. Если деформация приводит к
более выгодному энергетически состоянию, ядро
будет спонтанно деформироваться вплоть до
деления на два фрагмента. Количественно такая
оценка может быть проведена следующим образом.
При деформации ядро – не меняя своего
объема – превращается в эллипсоид с осями
a = R(1 + ), b =
(1 - /2); V = 4
R3/3 = 4ab2/3.
При деформации не меняется первый член формулы Вайцзеккера (1.11) , второй (поверхностная энергия) по абсолютной величине возрастает, а третий (кулоновская энергии) – уменьшается:
| Es = a2A2/3(1 + 22/5 + ...); EC = a3Z2A-1/3(1 - 2/5 + ...). |
(1.12) |
Таким образом, деформация изменяет полную энергию ядра на величину
| E =
-2(2a2A2/3
- a3Z2A-1/3). |
(1.13) |
( Здесь учтен знак второго и третьего членов в
(1.11))
Если величина изменения энергии (1.13)
положительна, энергия связи ядра будет расти, т.е.
деформация будет энергетически выгодна и
спонтанное деление возможно. Следовательно,
барьер деления будет исчезать, когда значения
(1.13) становятся больше нуля, что наступает при
значениях
| Z2/A > 2a2/a348. |
(1.14) |
(Следует подчеркнуть приближенный характер полученного результата как следствия классического подхода к квантовой системе - ядру)
Спин ядра и моменты нуклонов
Основное и возбужденные состояния ядра и других квантовых систем характеризуется набором квантовых чисел, являющихся собственными значениями операторов физических величин. Квантовый оператор F называется собственным оператором, если его действие на волновую функцию системы приводит к той же волновой функции, умноженной на число - собственное значение оператора:
= f.
Примерами таких операторов являются
оператор квадрата момента количества движения
квантовой системы и оператор проекции момента
количества движения на выделенную ось.
Собственные значения операторов физических
величин сохраняются или, как иногда говорят,
являются хорошими квантовыми
числами, если соответствующий оператор
коммутирует с полным гамильтонианом квантовой
системы.
Если ядро близко к сферическому,
соответствующий ему гамильтониан коммутирует с
оператором квадрата момента. Это означает, что
собственные значения этого оператора являются
“хорошими квантовыми числами”, т.е. сохраняются.
Как правило, ядерный гамильтониан коммутирует
также с оператором проекции момента на одну из
осей ( в качестве этой оси обычно выбирают ось z):
[ , 2] = 0; [,z]
= 0. |
(1.15) |
Все перечисленные операторы действуют в
пространстве волновых функций ядра :
| 2 = J(J + 1);z = m, m = -J, -J+1,..., J-1, J. |
(1.16) |
Спином ядра называется максимальное
собственное значение проекции момента на ось,
т.е. величина J. Спины и моменты частиц и ядер
измеряются в единицах 
.
Спин нуклона равен 1/2.
Полный момент количества движения
нуклона в ядре складывается из его спина и
орбитального момента относительно центра ядра:
= 
+ 
= + 
.
Спин ядра – результат сложения моментов нуклонов ядра:
 |
(1.17) |
Изоспин ядер и нуклонов
Как основное, так и возбужденные
состояния ядер - помимо рассмотренных выше энергии,
спина и четности – характеризуются квантовыми
числами, которые называются изоспином
и проекцией изоспина. (В
литературе эти квантовые числа обозначаются
обычно либо символами T и Tz, либо I и Iz ).
Введение этих квантовых чисел связано
с тем фактом, что ядерные силы инвариантны
относительно замены протонов на нейтроны. Это
особенно ярко проявляется в спектрах т.н.
”зеркальных” ядер, т.е. ядер–изобар, у которых
число протонов одного равно числу нейтронов
другого. Для всех известных пар таких ядер имеет
место подобие спектров низших возбужденных
состояний: спины и четности низших состояний
одинаковы, а энергии возбуждения близки.
С точки зрения теории изоспина,
нейтрон и протон являются одной и той же частицей
– нуклоном с изоспином I = 1/2 – в двух разных
состояниях, различающихся проекцией изоспина на
выделенную ось (Iz= I3) в пространстве
изоспина. Таких проекций для момента
I = 1/2 может быть только две: Iz = +1/2
(протон) и
Система Z протонов и N нейтронов – ядро - имеет проекцию изоспина
| Iz(A,Z) = Z.(+1/2) + N.(-1/2) = (Z - N)/2. | (1.18) |
Изоспин системы нуклонов является векторной суммой изоспинов составляющих:
 . |
(1.19) |
Ядерные (т.е. сильные) взаимодействия
не зависят от проекции изоспина, или, точнее, сильные
взаимодействия инвариантны относительно
вращений в изоспиновом пространстве.
Однако от величины изоспина ядерные
силы зависят! Низшим по энергии состояниям
системы нуклонов, т.е. основным состоянием ядра,
является состояние с возможным низшим значением
изоспина, которое равно
| I0 = |Iz| = |(Z - N)/2|. | (1.20) |
Возбужденные состояния ядер могут
иметь более высокие значения изоспина, но с той
же проекцией.
Таким образом, характеристиками
уровней данного ядра являются энергия, спин
состояния, четность состояния и изоспин. Обычно
три последних квантовых числа указываются как JP,I.
Спектры ядер
 Рис. 1.3. Спектр ядра 12С. Заштрихована область непрерывного спектра. |
На схемах спектров ядер указывают
энергии уровней ядра в МэВ или в кэВ, а также спин
и четность состояний. На современных схемах
указывают также изоспин состояний. (Поскольку на
схемах спектров даны энергии возбуждения
уровней, энергия основного состояния
принимается за начало отсчета). В области энергий
возбуждения E < Eотд – т.е. при
энергиях, меньших, чем энергия отделения нуклона,
спектры ядер – дискретные. Это означает, что
ширины спектральных уровней меньше расстояния
между уровнями Г < E.
Спонтанные переходы ядер из более
высоких возбужденных состояний дискретного
спектра ядра в более низкие ( в том числе в
основное состояние) реализуются, как правило,
путем излучения гамма-квантов, т.е. за счет электромагнитных взаимодействий.
В области больших энергий возбуждения, когда
E > Eотд, ширины уровней
возбужденного ядра резко возрастают. Дело в том,
что в отделении нуклона от ядра главную роль
играют ядерные силы- т.е. сильные
взаимодействия. Вероятность сильных
взаимодействий на порядки выше вероятности
электромагнитных, поэтому ширины распада по
сильным взаимодействиям велики и уровни ядерных
спектров в области E > Eотд перекрываются
– спектр ядра становится непрерывным. Главным
механизмом распада высоковозбужденных
состояний с этой области энергий является
испускание нуклонов и кластеров (альфа-частиц и
дейтронов). Излучение гамма-квантов в этой
области высоких энергий возбуждения E > Eотд
происходит с меньшей вероятностью, чем
испускание нуклонов. Возбужденное ядро имеет,
как правило, несколько путей, или каналов,
распада. На рис. 1.3 показан спектр ядра 12С.
Спектр выше 16 МэВ – непрерывный.
Электромагнитные моменты нуклонов и ядер
Электромагнитные моменты определяют потенциал взаимодействия ядра или частиц с внешними электрическими и магнитными полями:
V = Ze - DiEi - Qij Ei/rj -  iBi
+ ... |
(1.21) |
Здесь Ze – заряд ядра, φ – электромагнитный потенциал, D – электрический дипольный момент ядра, Q – квадрупольный момент ядра, μ – магнитный дипольный момент. Более высокие по тензорной размерности члены потенциала взаимодействия (1.21) дают пренебрежимо малый вклад во взаимодействие.
Электрический дипольный момент ядер в основном состоянии равен нулю (с точностью до малых членов, связанных со слабыми взаимодействиями в ядрах). Равенство нулю момента Di является следствием четности квадрата волновой функции основного состояния ядра:
Die = Ze ri|0( )|2dv;Dze = Ze z|0()|2dv. |
(1.22) |
Квадрат волновой функции основного
состояния ядра является четной функцией
координат, z – нечетная функция. Интеграл по
трехмерному пространству от произведения четной
и нечетной функций всегда равен 0 (Квадрат -функции имеет
положительную четность в случае, если сама -функция имеет определенную
четность(+ или -). Это справедливо для вкладов в -функцию от сильных и
электромагнитных взаимодействий, сохраняющих
четность. Малые добавки в -функцию
от слабых (не сохраняющих четность)
взаимодействий могут дать отклонение от нуля для
дипольных моментов ядер и частиц. Роль этих
вкладов представляет большой интерес для
современной физики, поэтому попытки измерить
дипольный момент нейтрона не прекращаются.
Квадрупольный электрический момент ядра в системе координат, связанной с ядром ( внутренний квадрупольный момент)
Qe = (3z2 - r2) ()dv;()dv = Ze|0|2dv = Ze. |
(1.23) |
Поскольку среднее значение
физической величины в квантовой механике, по
определению, 
,
внутренний квадрупольный момент, с точностью до
констант, есть разность среднего значения
величины 2z2 и среднего значения суммы
квадратов x2 и y2 . Поэтому для
сферических ядер Q = 0, для вытянутых
относительно внутренней оси вращения z Q > 0
, а для сплюснутых Q < 0.
Магнитный дипольный момент
Магнитный дипольный момент частицы является оператором в пространстве волновых функций частиц и связан с операторами орбитального и спинового моментов соотношением
 |
(1.24) |
Здесь m – масса частицы, e/2mc
- магнетон. (Магнетон Бора для электронов и
ядерный магнетон с m = mp для протона и
нейтрона)
Гиромагнитные отношения для
электрона, протона и нейтрона приведены в
таблице
| e | p | n | |
| gl | -1 | 1 | 0 |
| gs | -2 | 2(2.793) | 2(-1.913) |
| Пример: Рассчитать значения магнитных моментов электрона, протона и нейтрона в системах координат, связанных с каждой из частиц. |
В системе координат, связанной с
частицей, орбитальное движение отсутствует.
Значение магнитного момента определяется как
диагональный матричный элемент оператора (1.24) в
состоянии с максимальным значением проекции
момента на ось z.
Действие оператора проекции спина
дает
  |
(1.25) |
Таким образом, для всех указанных частиц значение магнитного дипольного момента в магнетонах равно половине гиромагнитного отношения gs. (Принято указывать значения магнитных моментов нуклонов и ядер в ядерных магнетонах
 = 3.152.10-14 МэВ .T-1;( B/N) = (mp/me) |
(1.26) |
Наблюдаемое значение магнитного момента ядра (в ядерных магнетонах) связано со значением спина ядра. Проекция квантового оператора магнитного момента на направление спина приводит к величине, являющейся – с точностью до коэффициента- оператором квадрата спина ядра:
 |
(1.27) |
Коэффициент gN называется
ядерным гиромагнитным отношением. Его
теоретическая величина может быть получена из
(1.27) путем расчета матричных элементов левой и
правой части равенства для ядерного состояния с
моментом j и проекцией момента +j. ( Cм. далее лекцию
3)
Одним из методов измерения величины
ядерного спина и магнитного момента ядра
является исследование сверхтонкого расщепления
линий атома.
Определим число линий сверхтонкого
расщепления, возникающее за счет взаимодействия
магнитного момента ядра с магнитным полем,
созданным электронной оболочкой атома.
Полный момент системы электронная
оболочка-ядро складывается из момента
электронной оболочки I и спина ядра J. Поскольку
величина магнитного поля, создаваемого
электронами в области ядра, пропорциональна I, а
магнитный момент ядра связан с J (1.27) , потенциал
взаимодействия является функцией скалярного
произведения этих векторов:
 =  +  ;Vint = a   = const.N(.). |
(1.28) |
Этот потенциал взаимодействия, входящий в полный гамильтониан атома, ответственен за тот экспериментальный факт, что состояния с разными значениями скалярного произведения векторов I и J имеют разные сдвиги в энергиях атомных уровней. Поскольку величина сдвига зависит от ядерного магнетона (1.28), она мала по сравнению с величиной тонкого расщепления атомных уровней, которые вызваны взаимодействием магнитного момента электронной оболочки с внешним магнитным полем. Поэтому расщепление атомных уровней, возникающее благодаря взаимодействию магнитного момента ядра с магнитным полем атома, называется сверхтонким. Число состояний сверхтонкого расщепления равно числу разных значений скалярного произведения векторов. Определим эту величину через квадраты квантовых векторов F, J, I:
| 2
= 2 + 2 + 2; =
(2 - 2 - 2). |
(1.29) |
Квадраты векторов F, J, I являются собственными операторами волновой функции атома, представляющей собой произведение волновых функций ядра и электронной оболочки
a
= N.e. |
(1.30) |
Таким образом, число уровней
сверхтонкого расщепления равно числу разных
значений квантового вектора = +
,
| F = |J-I|, |J-I+1|,..., J+I-1, J+I. | (1.31) |
Число разных значений вектора F равно 2К + 1, где К – наименьший из векторов J, I.
