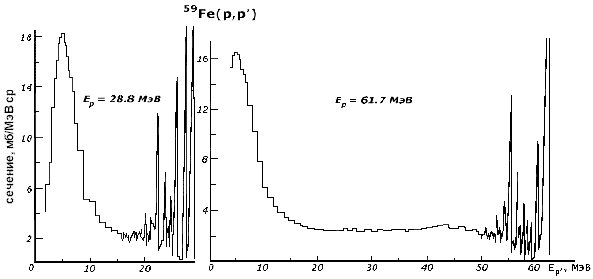
Первой моделью ядра была капельная модель, развитая в работах Н. Бора, Дж. Уиллера и Я. Френкеля. В этой модели атомное ядро рассматривается как сферическая капля заряженной жидкости. Основанием для такой аналогии послужило то, что плотность ядерного вещества у всех ядер вблизи линии стабильности приблизительно одинакова, что говорит о его несжимаемости. Кроме того, с жидкостью ядерное вещество сближает и свойство насыщения ядерных сил (энергия связи ядер приблизительно пропорциональна массовому числу). В рамках капельной модели удалось объяснить многие свойства атомного ядра и получить полуэмпирическую формулу для энергии связи атомных ядер (формула Вайцзеккера), которая позволила понять некоторые закономерности в α- и β-распадах, делении ядер и грубо оценивать массы и энергии связи новых ядер
Eсв = a1A - a2A2/3 - a3Z2/A1/3 - a4(A/2 - Z)2/A + a5A-3/4,
где a1 = 15,75 МэВ; a2 = 17,8 МэВ; a3 = 0,71 МэВ; a4 = 94,8 МэВ;
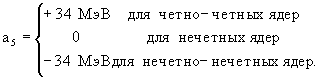
|
|
Экспериментальные исследования выявили некоторую
периодичность в изменении индивидуальных характеристик основных и возбужденных
состояний ядер (таких, как энергии связи, спины, магнитные моменты, четности,
некоторые особенности α- и β- распада, размещение ядер-изомеров среди остальных
ядер и др.). Эту периодичность капельная модель описать была не способна (см.
рис.4).
Отмеченная периодичность подобна периодичности свойств
электронных оболочек атома и определяется магическими числами нейтронов и
протонов:
n |
2, 8, 20, 28, 50, 82, 126, 184 |
p |
2, 8, 20, 28, 50, 82, 114 |
Магические числа нейтронов и протонов по аналогии с атомами соответствуют
полностью заполненным оболочкам. Различие в магических числах - 126 (для
нейтронов) и 114 (для протонов) - обусловлено кулоновским взаимодействием.
Впервые на особую устойчивость ядер с магическим числом
нейтронов или протонов обратили внимание
Дж.
Бартлетт (1932 г.) и
В. Эльзассер (1933
г.). Эльзассер попытался понять стабильность магических ядер, предполагая, что
нуклоны, подобно электронам в атоме, движутся независимо друг от друга в
одночастичной потенциальной яме. Однако он смог объяснить только три первых
магических числа: 2, 8 и 20. Работа Эльзассера осталась незамеченной, так как в
то время еще не было накоплено достаточно экспериментальных данных и, кроме
того, его предположение казалось совершенно невероятным, поскольку в ядре, в
отличие от атома, нет выделенного силового центра, а короткодействующий характер
ядерных сил, казалось бы, исключал введение результирующего среднего потенциала.
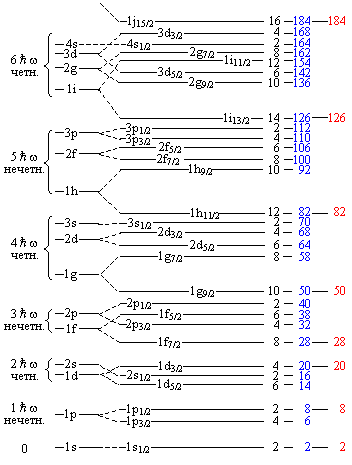
Рис. 5. Одночастичные уровни в оболочечном потенциале. |
С течением времени, однако, накапливались все новые и
новые экспериментальные доказательства существования оболочечной структуры ядер.
Однако все предложенные варианты потенциальной ямы не давали правильных значений
магических чисел.. Наконец, в 1949 г.
М. Гепперт-Майер
и Дж. Йенсен сделали решающий шаг
в становлении оболочечной модели. Они поняли, что для объяснения заполнения
ядерных оболочек при N, Z = 50, 82 и N = 126, необходимо учесть так называемое
спин-орбитальное взаимодействие: взаимодействие спина нуклона с его орбитальным
моментом количества движения. Благодаря этому им удалось воспроизвести
наблюдаемые в эксперименте магические числа нуклонов. Далее они указали на
важность учета принципа Паули при рассмотрении движения нуклона в ядре: принцип
Паули препятствует потере энергии нуклоном при столкновении, так как все
низколежащие одночастичные состояния заняты, поэтому средняя длина свободного
пробега нуклона оказывается больше размеров ядра, что позволяет говорить об
индивидуальных орбитах нуклонов. В модели оболочек предполагается, что нуклоны
движутся независимо друг от друга в сферически-симметричной потенциальной яме.
Собственные состояния нуклона в такой яме находят, решая соответствующее
уравнение Шредингера. Эти состояния характеризуются квантовыми числами, которые
определяют физические величины, сохраняющиеся при движении в
сферически-симметричном поле (рис.5).
В оболочечной модели спин ядра складывается из суммы спинов и
орбитальных моментов отдельных нуклонов. Принцип Паули и специфика ядерного взаимодействия
приводят к тому, что все четно-четные ядра имеют спин равный 0. Четность
состояния определяется произведением внутренних четностей составляющих его
частиц на четности волновых функций, описывающих их движение относительно общего
центра инерции. Внутренняя четность нуклонов принята положительной. Таким
образом для четности ядерного состояния справедливо выражение
![]() ,
,
где li - орбитальный момент i-го нуклона, A - количество нуклонов
в ядре
Оболочечная модель во многих случаях хорошо воспроизводит
экспериментальные значения спинов и четностей, электрических квадрупольных и
магнитных моментов атомных ядер, средние времена жизни ![]() -активных ядер, объясняет распределение
ядер изомеров.
-активных ядер, объясняет распределение
ядер изомеров.
Наилучшие предсказания оболочечная модель дает для ядер
вблизи заполненных оболочек, для которых самосогласованный потенциал
сферически-симметричный. Однако в атомном ядре наблюдаются возбужденные
состояния и другого типа - многонуклонные возбужденные состояния, в которых
движение отдельных нуклонов скоррелировано. Это колебательные и вращательные
возбуждения атомных ядер (рис.6 - 7).
Когерентные колебания протонов относительно нейтронов
называются гигантскими резонансами. Наиболее изученный из них гигантский
дипольный резонанс. Он наблюдается во всех ядрах. Феноменологическая теория
колебательных состояний атомных ядер была разработана
О. Бором
(1952 г.).
Рис. 6. Колебания ядра: а - монопольная объемная мода, б - квадрупольная поверхностная мода, в - нейтрон-протонные поляризационные колебания |
По мере удаления от заполненных оболочек минимум потенциальной энергии может соответствовать деформированному ядру. У несферического ядра изменяются одночастичные уровни, меняется частота колебаний, появляются вращательные степени свободы. Энергия вращательных состояний четно-четных деформированных аксиально-симметричных ядер описывается соотношением
![]() ,
,
где ![]() -
момент инерции ядра, J - спин ядра, пробегающий целочисленные значения (рис.7).
-
момент инерции ядра, J - спин ядра, пробегающий целочисленные значения (рис.7).
Рис. 7. Вращательный спектр сильно деформированного ядра 170Hf |
Модель, которая позволила бы одновременно учесть как одночастичные так и коллективные степени свободы ядра - обобщенная модель была предложена в начале 50-х годов Д. Рейнуотером, О. Бором и Б. Моттельсоном. В этой модели предполагается сильная связь внешних по отношению к заполненным оболочкам нуклонов с остовом, что может приводить к устойчивой равновесной деформации ядра. Движение остова описывается в гидродинамической модели. Одночастичные состояния рассчитываются в деформированном потенциале. Впервые такие расчеты одночастичных состояний с использованием деформированного аксиально-симметричного потенциала были выполнены в 1955 году С. Нильссоном (рис.8).
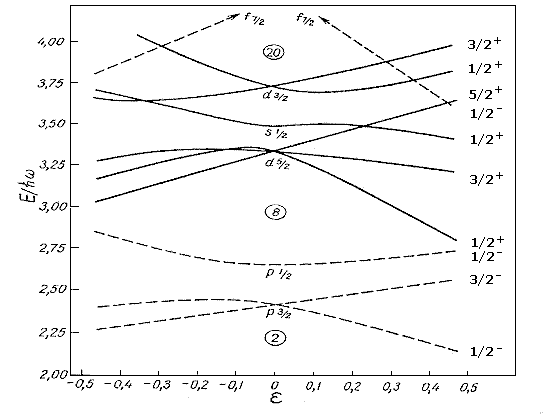 Рис. 8.
Одночастичные уровни энергии в потенциале Нильссона Рис. 8.
Одночастичные уровни энергии в потенциале Нильссона |
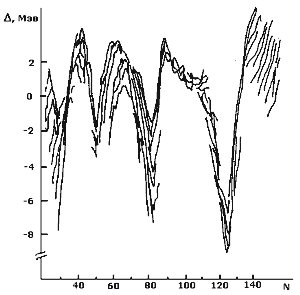
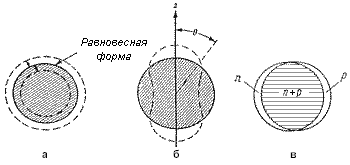

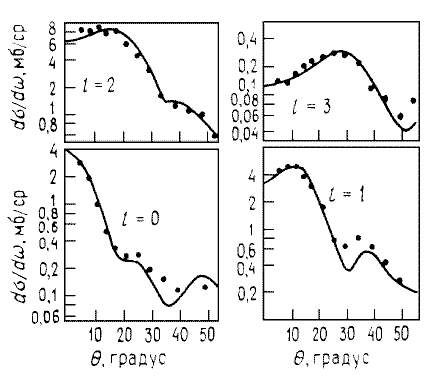 Рис. 10.
Экспериментальные угловые распределения для различных состояний конечного
ядра 59Ni, возбуждаемых в реакции 58Ni(d,p)59Ni
при энергии Ed = 15 МэВ, и результаты расчетов по методу искаженных волн.
Все четыре случая различаются передачей орбитального момента l
Рис. 10.
Экспериментальные угловые распределения для различных состояний конечного
ядра 59Ni, возбуждаемых в реакции 58Ni(d,p)59Ni
при энергии Ed = 15 МэВ, и результаты расчетов по методу искаженных волн.
Все четыре случая различаются передачей орбитального момента l