Атомные ядра являются связанной системой взаимодействующих протонов и нейтронов. В атомном ядре проявляются три типа взаимодействий.

• Сильные взаимодействия между нуклонами приводят к образованию связанного состояния A нуклонов.
• Электромагнитные взаимодействия приводят с одной стороны к расталкиванию между протонами, что ослабляет связь в атомном ядре, с другой стороны взаимодействие магнитных моментов нуклонов приводит к большому разнообразию ядерных состояний.
• Слабое взаимодействие между нуклонами приводит к взаимным превращениям нейтронов и протонов в атомном ядре − явлению β-распада атомных ядер.

    В основе всех моделей строения вещества до открытия нейтрона господствовала концепция электрического строения вещества. Электрическое взаимодействие связывало атомное ядро и электроны атомных оболочек. Атомное ядро считалось состоящим из протонов и электронов. Факт вылета из ядра электронов при β-распаде считался несомненным доказательством того, что электроны находятся в ядре. Даже предсказанная Резерфордом нейтральная частица, которая была открыта Чадвиком, считалась сильно связанным состоянием протона и электрона.
    Ситуация изменилась, когда пришло понимание, что нейтрон является такой же элементарной частицей как и протон.
    Было очевидно, что протон-нейтронную модель ядра по аналогии с моделью атома необходимо создавать на основе законов квантовой теории. Однако оставался открытым вопрос о том, какие силы связывают протоны и нейтроны в ядре. Изучение свойств ядерных сил стало центральной задачей ядерной физики. Было очевидно, что это силы не электрической природы, что они действуют на расстоянии меньше 10^–12 см, что это силы притяжения, о чем свидетельствовало существование связанной системы – дейтрон, состоящей из протона и нейтрона. Дейтрон имеет размер ~2,3 фм и энергию связи 2,2 МэВ. Атомные ядра имеют радиусы от 2 до 8 фм. Энергия связи, приходящаяся на один нуклон для большинства атомных ядер, составляет от 5 до 9 МэВ. Ядерные силы, связывающие протоны и нейтроны в ядре в тысячи раз превосходят электромагнитные силы на расстояниях ядерных масштабов.
    Возникло представление о новом типе взаимодействий – ядерном взаимодействии, которое связывает протоны и нейтроны в атомные ядра.
    Представление о протон-нейтронном составе атомных ядер поставило задачу выяснения особенностей сил, связывающих протоны и нейтроны. Такие силы, получившие название ядерных сил, был неизвестны. Теоретическое описание таких сил столкнулось с трудностями, так как

• Ядро состоит из сравнительно большого числа нуклонов, поэтому было очевидно, что решение должно быть получено с использованием приближенных методов.
• Свойства ядерных сил, особенно на малых расстояниях, были неизвестны.

    Ядерное взаимодействие. Потенциал.

    Г. Гамов, 1932 г.: «Как хорошо известно, масса какого-либо ядра не равна сумме масс входящих в его состав протонов и электронов, а меньше последней на некоторую величину ∆М, носящую название полного дефекта массы и связанную с полной энергией внутренней связи ядра релятивистским соотношением:

E = ∆М∙c²,

где c скорость света. Точные измерения атомных весов различных изотопов, которыми мы обязаны, главным образом, работам Астона (Aston), дают нам возможность вычислить эти энергии связи для целого ряда ядер. В первом приближении мы можем считать полную энергии связи пропорциональной числу составных частей ядра. Само собой напрашивается, однако, предположение, что в сложных ядрах элементарные его составные части (протоны и электроны) соединяются в некоторые устойчивые образования, играющие и сложных ядрах самостоятельную роль. Такими единицами второго порядка могут, например, являться недавно открытые простейшие ядра-нейтроны (протон + электрон), ядра водородного изотопа (два протона + электрон) и, наконец, давно известные, чрезвычайно устойчивые ядра гелия или α-частицы (четыре протона + два электрона). Делая определенные гипотезы о составе ядра, мы можем получить энергию, связывающую между собой эти составные части, вычитая из полной энергии ядра внутреннюю энергию этих образований.
    Совершенно новым предположением относительно составных частей ядра является предположение, бывшее непосредственным следствием открытия нейтронов, согласно которому каждый ядерный электрон связан в первую голову с одним из ядерных протонов, образуя нейтрон. Таким образом мы имеем в ядре Z протонов и A – Z нейтронов, которые, в свою очередь, соединяясь в группы по две пары, образуют α-частицы. Таким образом мы получаем следующий состав ядра: для четного атомного номера Z/2 α-частиц и A – 2Z нейтронов; для нечетного атомного номера Z/2 – 1 α-частиц, А – 2Z + 1 нейтрона и один протон. Мы видим, что при таком предположении число α-частиц в тяжелых ядрах будет несколько меньше, чем при прежнем предположении (например, для ртути Z = 80, А = 200, число α-частиц согласно новой гипотезе, равно всего 40 вместо 50).
    Перейдем теперь к рассмотрению вопроса об устойчивости атомного ядра по отношению к различным преобразованиям. Для этого необходимо прежде всего сделать определенные предположения о характере взаимодействия между различными составными частями ядра. Для взаимодействия двух протонов, которые мы можем здесь рассматривать как точечные заряды (поскольку радиус протона r_p = e²/m_pc² = 2·10^-16 см значительно меньше радиуса ядра), мы можем спокойно принять кулоновские силы отталкивания с потенциалом.
    Взаимодействие между протоном и нейтроном, или же между двумя нейтронами будет, очевидно, сказываться лишь на расстояниях, сравнимых с размерами нейтрона (т. е. несколько ×10^-13 см) и весьма быстро спадать при удалении частиц.
    Пользуясь аналогией, взятой из области взаимодействия атомов и ионов, мы можем предположить, что в обоих случаях будут иметь место силы притяжения, причем при взаимодействии протона с нейтроном взаимная потенциальная энергия – I(r) будет значительно больше, нежели энергия – K(r), соответствующая взаимодействию двух нейтронов. Здесь необходимо указать, что относительно потенциалов – I(r) и – K(r) нужно сделать еще одно добавочное предположение, а именно: при слишком уже тесном сближении частиц эти потенциалы должны начать возрастать; давая начало силам отталкивания, ибо в противном случае модель ядра не будет устойчивой, обнаруживая тенденцию стянуться в точку.
    Что касается взаимодействия между α-частицами, то оно будет, очевидно, слагаться из кулоновского отталкивания и из средней силы перекрестного взаимодействия входящих в их состав протонов и нейтронов, Последнее приводит, как можно показать, к притяжению с потенциальной энергией,, близкой к взаимодействию нейтронов (силы, связанные с потенциалом I(r), взаимно уничтожаются), так что мы можем написать для потенциальной энергии двух α-частиц:

4e²/r - L(r),

где L(r) = K(r) также, весьма быстро убывает с расстоянием.

    Рассмотрим теперь, как будет вести себя совокупность таких частиц с массами примерно одного порядка, притягивающихся друг к другу с силами, весьма быстро убывающими с расстоянием (кулоновскими силами отталкивания внутри ядра можно в первом приближении пренебречь). Состояние такой системы должно быть весьма аналогично тому, что мы имеем в небольшой капле жидкости, где внутри силы, действующие на какую-либо частицу, уравновешиваются (ибо радиус действия сил меньше радиуса, ядрах), а вблизи поверхности возникают мощные силы, препятствующие частице покинуть каплю (поверхностное натяжение). Хотя точного решения задачи о такой совокупности до сих пор не имеется, мы можем сделать ряд интересных заключений о свойствах такой модели. Прежде всего, мы должны предположить, что объем такой модели будет примерно пропорционален числу частиц, так что радиус будет изменяться примерно как кубический корень из атомного веса. Потенциальная энергия для данной частицы внутри такой модели должна быть более или менее постоянной и резко возрастать у границ, образуя, таким образом, своего рода «потенциальную яму».
    Из вышесказанного о характере сил взаимодействия между различными частицами в ядре следует, что «дно» этой «ямы» для протона будет лежать значительно ниже, нежели для нейтронов или α-частиц. Полная энергия такой модели должна быть примерно пропорциональна числу частиц. Мы не должны, однако, забывать о наличии сил кулоновского отталкивания. Эти силы не могут изменить существенно распределения потенциала внутри ядра, где главную роль играют силы притяжения. Однако эти силы принизят значения потенциала на больших расстояниях и приведут к образованию вокруг ядра потенциального барьера, играющего столь важную роль в теории ядерных превращений. Это поднятие потенциальной ямы относительно значения потенциала в бесконечности будет, очевидно, совершенно отсутствовать для нейтронов, лишенных заряда, а для протока будет в два раза меньше; чем для α-частицы. Распределение потенциала в ядре при учете кулоновских сил указано на рисунке, где взят случай тяжелого ядра, в котором уровень α-частицы уже поднялся выше нулевого уровня, обусловливая этим возможность самопроизвольного α-распада.
    До сих пор мы рассматривали находящиеся в ядре нейтроны как неделимые, единицы, и поэтому могли строить модель ядра на основе привычной механики. Теперь мы обратимся к распадению ядерного нейтрона на протон и электрон и выбрасыванию этого последнего за пределы атома, т. е. к столь загадочному явлению β-распада.
    Как хорошо известно, β-распад представляет один из наиболее резких примеров неповиновения электрона всем принципам современной теории. В то время как при ядерных реакциях с участием тяжелых частиц мы всегда имеем дело с резко выраженными квантовыми уровнями и строгим соблюдением баланса энергии, в случае β-превращений – ни то, ни другое не имеет места. Как показали экспериментальные исследования Эллиса (Ellis), электроны, выбрасываемые при распаде различными атомами, одного и того же вещества, имеют самые разнообразные значения энергии, изменяющиеся непрерывно между нулем и как угодно большими значениями, причем кривая распределения имеет вид, весьма сходный с кривой ошибок. Какое-либо другое излучение, могущее компенсировать созданную таким образом разность энергии между различными ядрами, полностью отсутствует, а между тем все свойства и дальнейшее поведение ядер до и после распада совершенно идентичны. С чисто экспериментальной точки зрения дело здесь выглядит так, как будто мы имеем дело с нарушением закона сохранения энергии. Кроме этого основного факта имеется еще целый ряд не менее основательных аргументов, говорящих, что с ядерными электронами дело плохо; сюда относятся, например, невязки в статистике ядер и величин их вращательных моментов. Причины всех этих непорядков лежат в том, что, как указал Бор (Bohr), мы здесь выходим уже за границы области, где можно применять классическое понятие электрона. В самом деле, для радиуса электрона мы имеем по классической теории значение

т. е. величину, сравнимую с размерами той области, где электрон вынужден двигаться, а при этих условиях такое грубее представление об электроне как заряженном шарике, конечно, не применимо.
    В связи с этим стоит тот факт, что, оценивая возможную скорость электрона в ядре согласно основам квантовой теории, мы приходим к величине, столь близкой к скорости света (0,9998 с), что о пренебрежении теорией относительности не может быть и речи, а между тем мы не имеем по сию пору релативистской теории квантов.
    Пока такая общая теория, являющаяся органическим синтезом современной нерелативистской теории квантов (волновой механики) и неквантовой релативистики, не будет построена, об истинном понимании процесса β-распада не может быть и речи. Однако уже сейчас мы можем пытаться строить рабочие теории β-распада, пользуясь старыми понятиями. Основное положение теории β-устойчивости и β-распада, предложенной недавно Гейзенбергом, заключается в том, что, закрывая глаза на неопределенность энергии β-частиц, необходимым и достаточным условием возможности распада принимается положительность соответствующего энергетического баланса.
    Рассмотрим ядро, состоящее исключительно из п «слипшихся» друг с другом нейтронов. Поскольку между нейтронами существуют лишь силы притяжения, такое ядро будет, конечно, устойчивым по отношению к нейтронам, т. е., извлекая из ядра нейтрон, мы затратим некоторую работу, которая, очевидно, будет порядка – K(r), где r – среднее расстояние между частицами в ядре. Вынутый нейтрон разложим на протон и электрон, на что потребуется работа, определяемая внутренней энергией связи нейтрона D (эта величина весьма незначительна и равна, согласно измерениям Чадвика, всего одному или двум миллионам вольт, тогда как энергии K(r) и I(r) измеряются десятками миллионов). Теперь вернем полученный протон ядру, получив при этом энергию порядка + I(r); поскольку |I(r) >> |K(r), то при таком процессе мы будем иметь положительный баланс энергии. Нетрудно, однако, видеть, что произведенная реакция эквивалентна просто выниманию из ядра одного электрона и, поскольку баланс энергии положителен, мы должны ожидать наличия самопроизвольного β-раcпада. Таким образом, первоначально нейтральное, ядро начнет испускать последовательный ряд β-частиц, общее число n₁ входящих в его состав нейтронов начнет уменьшаться, давая начало все большему числу n₂ протонов. Однако этот процесс не дойдет до конца; ввиду возрастания положительного заряда ядра, введению в него новых протонов будут противодействовать кулоновские силы отталкивания, и наконец, «замена нейтрона протоном» сделается заменой энергетически невыгодной».

    Ядерное взаимодействие. Обмен частицами. В 1934 г. с взаимными ссылками Д. Иваненко и И. Тамм опубликовали работы, в которой они впервые рассмотрели ядерные силы как обмен электроном и антинейтрино. Это были первые работы, в которых ядерные силы рассматривались как обмен частицей с массой отличной от нуля. Это фактически означало, что в отличие от гравитационного и электромагнитного излучения радиус действия не бесконечен. Однако, естественно массы электрона не хватало для того, чтобы правильно описать радиус действия ядерных сил.

    И. Тамм: «Ферми недавно развил теорию β-радиоактивности, основанную на предположе­нии о возможном превращении нейтрона в протон и наоборот, сопровождающемся возникновением или исчезновением электрона и нейтрино.
    В этой теории можно получить обменные силы между нейтроном и протоном, введенные Гейзенбергом более или менее феноменологически. (Та же идея, со­вершенно независимо, возникла у моего друга Д. Иваненко, с которым я имел возможность обсуждать этот вопрос).
    Рассмотрим две тяжелые частицы a и b, где a означает состояние нейтрона, а b − протона. Если а станет протоном, а b − нейтроном, то энергия не изменится. Эти два вырожденных состояния данной системы могут быть связаны двухступенчатым процессом − излучением электрона и нейтрино нейтроном а, который тем самым превращается в протон, с последующим поглощением этих легких частиц протоном b, который становится нейтроном. В промежуточном состоянии энергия этой системы в общем не сохраняется (ср. с теорией дисперсии). Также может иметь место излучение и поглощение позитрона и нейтрино. Таким образом, два вырожденных состояния рассматриваемой системы расщепляются на два энергетических состояния, различающихся знаком обменной энергии».

    Решающий шаг в развитии концепции ядерных сил как обмена массивной частицей был сделан Х. Юкава. В 1935 г. Х. Юкава предположил по аналогии с электромагнитным взаимодействием, что ядерные силы обусловлены существованием новой частицы, переносящей ядерное взаимодействие. Массу этой частицы ≈ 150 МэВ он оценил, исходя из радиуса действия ядерных сил.
    Открытие π-мезона в 1947 г. явилось подтверждением правильности идеи Х. Юкава. Ядерные силы – новый тип взаимодействий в физике. Ядерные силы оказались гораздо более сложными по сравнению с электромагнитными и гравитационными. Ядерные силы, имеющие характер притяжения на расстоянии ~ 1 ÷ 5 Ферми, сменяются силами отталкивания на расстоянии < 0,5 Ферми.

Радиальная зависимость нуклон-нуклонного потенциала

Однопионное np-взаимодействие

    Концепция мезонного обмена особенно хорошо работает на сравнительно больших расстояниях (>2 Фм), на которых можно не учитывать внутреннюю структуру мезонов и рассматривать их как точечные частицы.
    На рисунке показана диаграмма np-взаимодействия, осуществляемого однопионным обменом. Эта диаграмма – простейшая из возможных диаграмм np-взаимодействия. В него в данном случае вовлечены только по одному валентному кварку каждого нуклона – d (нейтрон) и u (протон).
    Используя связь между радиусом сил а и массой m переносчика взаимодействия

а = ћ/mc,

которая следует из соотношения неопределенностей для виртуальной частицы, получаем при характерном ядерном расстоянии а ≈ 1.5 Фм

Х. Юкава, 1935 г.: «На данном этапе развития квантовой теории ещё очень мало известно о природе взаимодействия элементарных частиц. Гейзенберг считал, что важную роль в строении ядра играет взаимодействие обменного типа между нейтроном и протоном. Недавно Ферми рассмотрел проблему β-распада на основе гипотезы о «нейтрино». Согласно этой теории нейтрон и протон могут взаимодействовать, излучая и поглощая пару частиц − нейтрино и электрон. К сожалению, энергия взаимодействия, вычисленная в этом предположении, чрезмерно мала по сравнению с энергией связи между нейтроном и протонами в ядре. Чтобы устранить данный недостаток, по-видимому, естественно видоизменить теорию Гейзенберга и Ферми следующим образом. Переход тяжелой частицы из состояния нейтрино в состояние протона не всегда сопровождается испусканием лёгких частиц, т.е. нейтрино и электрона, но иногда энергия, освобождаемая при переходе, поглощается другой тяжелой частицей, которая в свою очередь переходит из состояния протона в состояние нейтрона. Если вероятностью последнего процесса больше, нежели вероятность первого, то взаимодействие между нейтроном и протоном будет гораздо сильнее, чем в случае рассмотренном Ферми, в то время как вероятностью испускания лёгких частиц существенно не изменится. Оказывается такое взаимодействие между элементарными частицами можно описать с помощью поля сил так же, как описывается электромагнитным полем взаимодействие заряженных частиц. Приведенные выше соображения показывают, что взаимодействие тяжелых частиц с этим полем значительно сильнее взаимодействия с ним лёгких частиц. В квантовой теории этому полю должен соответствовать новый тип квантов подобно тому, как электромагнитному полю соответ­ствует фотон… Потенциал взаимодействия между нейтроном и протоном должен быть не кулоновским, но убывающим по мере увеличения расстояния гораздо быстрее. Это можно выразить, например, функцией ±g²e^-λr/r где g − постоянная с размерностью электрического заряда, λ − постоянная с размерностью см^-1. Константы g и λ должны быть определены путем сравнения с экспериментальными данными… Приблизительный расчет показывает, что теоретические значения совпадают с результатами эксперимента, если принять λ = 10¹²÷10¹³ см^-1, а для g значение в несколько раз превышающее заряд электрона, хотя никакой прямой зависимости между g и e в приведенных выше рассуждениях не предполагалось… Положив λ = 5·10¹² см^-1, получаем для m значение в 2·10² раз превышающее массу электрона. Поскольку квант с такой большой массой и положительным или отрицательным зарядом никогда не наблюдался, изложенная теория находится, по-видимому, на неверном пути. Однако мы в состоянии показать, что в условиях обычных ядерных превращений подобный квант не может быть излучен во внешнее пространство.

1935 г. Х. Юкава разработал теорию ядерного взаимодействия и предсказал частицу, связывающую протоны и нейтроны в ядре.

Хидеки Юкава (1907 –1981)

Диаграммы N-N взаимодействий

    Пионы описывают NN взаимодействие на расстояниях 1.5 – 2 Фм. На меньших расстояниях должен происходить обмен более тяжёлыми мезонами − ω (m_ωc² = 782 МэВ), η (m_ηc² = 549 МэВ) и ρ (m_ρc²=770 МэВ). Особую роль в этой области расстояний играет обмен ω мезоном. Характер взаимодействия зависит от спина частицы, переносящей взаимодействие. Обмен векторными частицами J = 1 приводит к отталкиванию между нуклонами. Это отталкивание является аналогом отталкивания двух одноимённых зарядов в электростатике. Обмен скалярными мезонами J = 0 приводит к притяжению между нуклонами.

Нобелевская премия по физике
1949 г. Х. Юкава
За предсказание существования мезонов на основе теоретических работ по ядерным силам

    Информацию о свойствах ядерных сил можно получить, изучая простейшую ядерную систему дейтрон или в экспериментах по рассеянию нуклона на нуклоне. Казалось, что, имея информацию о ядерных силах, действующих между нуклонами, проблему структуры атомных ядер в принципе можно свести к задаче решения уравнения Шредингера для системы A частиц. Однако было очевидно, что такая задача в общем случае не может быть решена. Каждое атомное ядро – уникальный физический объект, имеющий присущие только ему специфические особенности. Взаимодействие нуклонов в ядре видоизменяется по сравнению с взаимодействием свободных нуклонов. Это различие обусловлено действием принципа Паули – в ядре проявляются такие особенности взаимодействия нуклонов, которых нет во взаимодействии свободных нуклонов. Кроме того, в ядерной системе проявляется многочастичный характер ядерных сил, приводящий к образованию в ядре кластерных образований. Наиболее яркий пример – образование α-кластеров в ядрах. Многие характеристики ядер с четным числом протонов и четным числом нейтронов отличаются от характеристик соседних ядер с нечетным числом нейтронов или протонов. Структура и свойства деформированных ядер отличаются от характеристик сферических ядер. Поэтому обычно используют различные модели атомных ядер. Большую роль в моделях атомных ядер играет концепция среднего ядерного поля и остаточного взаимодействия, не включенного в среднее поле. На основе этой концепции удалось объяснить, почему свойства ядер, имеющих близкие значения чисел протонов и нейтронов, сильно различаются друг от друга. В микроскопических расчетах среднее поле выбирается в виде потенциала Вудса-Саксона. Парные взаимодействия между нуклонами объясняют нулевое значение спина всех четно-четных ядер. Спин-орбитальное взаимодействие между нуклонами совместно с принципом Паули объясняют последовательность заполнения нуклонных оболочек
    Существует несколько моделей ядерной структуры, которые на первый взгляд кажутся противоречащими друг другу. Однако эти модели вовсе не исключают друг друга, а касаются различных свойств ядра и поэтому дополняют друг друга. Каждая модель ядра основывается на экспериментальных фактах и позволяет объяснить некоторые их выделенные свойства. Несмотря на то, что ядерные модели имеют ограниченную область применения, тем не менее, они играют важную роль в развитии теории ядра и в их рамках получен ряд существенных результатов.

    Модель жидкой капли. Одной из первых моделей атомного ядра была модель жидкой капли, в которой атомное ядро рассматривалось как сферическая капля несжимаемой ядерной жидкости радиуса R ≈ 1.3 Фм. Точные измерения показали, что вес ядра не равен сумме весов, входящих в состав ядра нуклонов, а меньше этой величины на несколько десятых процента. Разность этих величин – энергия связи ядра – энергия, необходимая для разделения ядра на отдельные нуклоны. В 1935 г. К. Вайцзеккер написал полуэмпирическую формулу для энергии связи ядер, в которой энергия связи ядра представлялась суммой объемной поверхностной и кулоновской энергий, энергии симметрии и энергии спаривания нуклонов

    Подбором коэффициентов α₁ – α₅, Вайцзеккеру удалось описать энергии связи стабильных ядер с точностью ~ 0.1%.
    Капельная модель дает правильное представление о массе и энергии связи ядра. На основе капельной модели можно рассчитать энергии распадов атомных ядер, получить зависимость между числом протонов и нейтронов в стабильных ядрах, грубо оценить области существования атомных ядер. Капельная модель ядра объяснила, почему максимум стабильности атомных ядер находится в районе ⁵⁶Fe. Наибольшим успехом капельной модели ядра явилась полуколичественная теория деления атомных ядер. Однако капельная модель столкнулась с рядом проблем, в частности, она была не в состоянии объяснить асимметрию массового распределения осколков деления – капельная модель предсказывает деление ядра на два осколка одинаковой массы. Вне компетенции капельной модели находятся описания спинов и четностей ядер

    Модель оболочек. Модель оболочек основывается на том, что свойства ядер, подобно свойствам атомов, обнаруживают определенную периодичность при изменении чисел протонов и нейтронов. На фоне довольно плавной зависимости энергии связи ядер от массового числа A встречаются ядра, в которых энергия связи больше чем в соседних ядрах. В этих ядрах также увеличена энергия отделения нуклона. Они имеют повышенную распространенность в природе. Такие ядра получили название магических, а числа протонов и нуклонов в них, соответствующие повышенной стабильности – магических чисел.

Магические числа 2, 8, 20, 28, 50, 82, 126.

    Ядра с магическим числом нейтронов имеют необыкновенно малое сечение поглощения нейтронов. Попытки построения моделей ядра, в которых нуклоны подобно электронам в атоме движутся независимо друг от друга в потенциальной яме, предпринимались неоднократно. Однако в таких моделях удавалось объяснить только первые три магических числа. Кроме того, независимое движение нуклонов в потенциальной яме казалось совершенно невозможным, т.к. в ядре в отличие от атома нет выделенного силового центра. Короткодействующий характер ядерных сил, казалось, исключал введение результирующего среднего поля. В 1949 г. М. Гепперт-Майер и Дж. Иенсен сделали решающий шаг в становлении оболочечной модели ядра. Они показали, что в ядерном потенциале необходимо учитывать спин-орбитальное взаимодействие нуклона – взаимодействие спина нуклона с его орбитальным моментом количества движения. Благодаря этому им удалось воспроизвести все магические числа. Они указали также на важность учета принципа Паули при рассмотрении движения нуклонов в ядре.

Энергия связи ядра
E_св(A,Z) = [Zm_p + (A - Z)m_n − M(A,Z)]c².

Формула Вайцзеккера
E_св(A,Z) = 15.75A − 17.8A^2/3 − 0.71Z(Z−1)/A^1/3 − 23.6(A − 2Z)²/A + a₅A^-3/4.

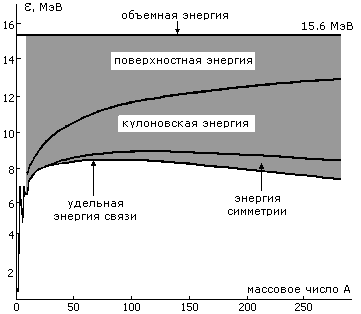
Вклад различных членов в удельную энергию связи ядра ε = E_св/A.

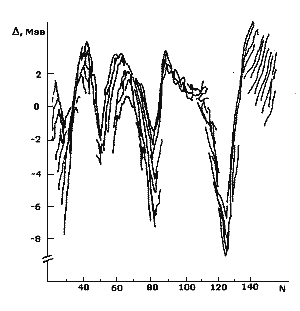
Разность Δ между предсказаниями формулы Вайцзеккера и экспериментальными значениями энергии связи ядер с различными числами нейтронов N. Наиболее сильные расхождения с экспериментальными значениями наблюдаются в окрестностях магических чисел нейтронов N = 20, 28, 50, 82, 126.

1948 г. Оболочечная модель ядра

Мария Гепперт-Майер (1906 – 1972)

Ханс Йенсен (1906 – 1973)

При учете спин-орбитального взаимодействия снимается вырождение по полному моменту j нуклона, который при данном l в зависимости от ориентации спина s относительно момента количества движения l принимает два значения j = l ± 1/2. Ниже по энергии опускается уровень j = l + 1/2, т.к. в этом случае нуклон сильнее взаимодействует с другими нуклонами ядра. В оболочечной модели ядра состояния нуклона описываются с помощью четырех квантовых чисел − n, l, j, j_z, где n − главное квантовое число, l − орбитальный момент нуклона, j − полный момент количества движения нуклона, j_z − проекция полного момента количества движения. В сферически симметричной системе состояния нуклона с разными значениями j_z вырождены.

Нобелевская премия по физике
1963 г. − М. Гепперт-Майер и Г. Йенсен
За открытия в области ядерной модели оболочек.

Модель оболочек

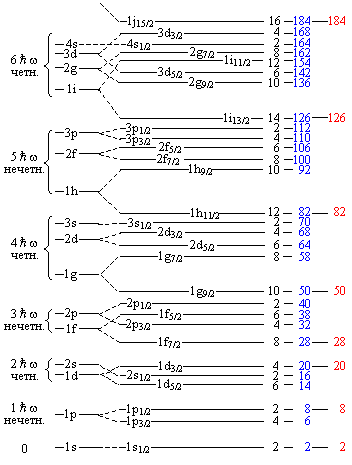
Одночастичные уровни в сферически-симметричном потенциале.

Нейтронные одночастичные состояния

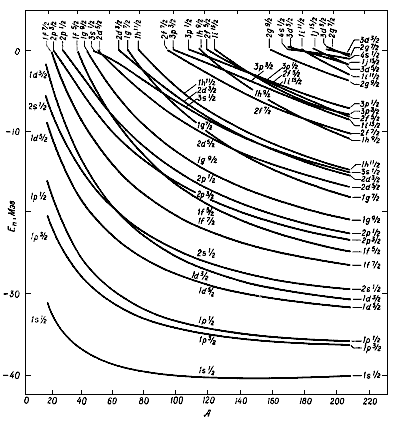
Зависимость энергии нейтронных одночастичных состояний от массового числа A сферически симметричных атомных ядер

    М. Гепперт-Майер: «Располагая уровни в надлежащем порядке, мы должны принимать во внимание спин-орбитальную связь. Орбиту отдельного нуклона нельзя уже полностью характеризовать лишь орбитальным импульсом l, нужно кроме l учесть еще и j = l ± ½ … Разность энергий двух уровней с одним и тем же l, но с разным j, растет с увеличением l. Предлагаемая модель подразумевает некоторые утверждения, которые можно сравнить с опытными данными. Речь идет о том, что ядро с замкнутой оболочкой протонов и нейтронов обладает равным нулю моментом импульса. Если добавить к ней еще один нуклон, то полный момент будет равен моменту этого одного нуклона. Мы можем предсказать по нашей схеме уровней, что это будет означать. Во всех случаях оказывается полное соответствие между предсказанием и результатами эксперимента».

    Возбужденные состояния атомных ядер. Много ценной информации о свойствах атомных ядер дает изучение возбужденных состояний атомных ядер. Средние и тяжелые ядра с достаточно хорошим приближением можно описать как состоящие из нуклонов, расположенных в заполненных оболочках – кор ядра, и нуклонов, находящихся во внешней незаполненной оболочке. Силы спаривания связывают нуклоны в пары с нулевым угловым моментом. Простейшим возбуждением ядра является одночастичный спектр, который обусловлен переходами неспаренного нуклона между уровнями незаполненной оболочки. Эффект спаривания нуклонов сыграл существенную роль в развитии модели оболочек, т.к. оказалось возможным объяснить многие свойства нечетных ядер, используя состояние последней нечетной частицы. Такие спектры наблюдаются в тех случаях, когда число нуклонов в незаполненной оболочке мало. Успехом модели оболочек было объяснение вероятности γ-переходов. Было показано, что вероятность γ-переходов увеличивается с увеличением энергии γ-перехода. Однако в ещё большей степени вероятность γ-переходов зависит от значений спинов и четностей состояний, между которыми происходит переход. Различают электрические и магнитные мультипольные переходы. Модель оболочек предсказала области изомерных состояний атомных ядер – острова изомерии.
    Наиболее просто выглядит спектр возбуждённых состояний ядер с одним нуклоном или «дыркой» сверх заполненных оболочек. Нижние возбуждения такого ядра образуются перемещением этого внешнего нуклона на более высокие подоболочки ядра. Примерами возбуждений такого типа являются нижние возбужденные состояния ядер и . Первое из этих ядер – это ядро с нейтронной дыркой в дважды магическом коре , второе – с одним нейтроном сверх этого же кора. В основном состоянии ядро ²⁰⁷Pb имеет одну вакансию (дырку) в подоболочке 3p_1/2. Поэтому спин J и четность основного состояния J^P(²⁰⁷Pb) = 3/2^-. Ядро ²⁰⁹Pb в основном состоянии имеет одну частицу на подоболочке 2g_9/2 сверх заполненного остова ²⁰⁸Pb. J^P(²⁰⁹Pb) = 9/2⁺. Возбужденные состояния в изотопах ²⁰⁷Pb и ²⁰⁹Pb обусловлены соответственно переходам нейтронной дырки (ядро ²⁰⁷Pb) или нейтрона (ядро ²⁰⁹Pb) между одночастичными уровнями при неизменном дважды магическом коре ²⁰⁸Pb (Z = 82, N = 126). Одночастичные переходы в ядре ²⁰⁹Pb происходят между одночастичными состояниями, расположенными над уровнем Ферми. В ядре ²⁰⁷Pb одночастичные переходы происходят одночастичными состояниями, расположенными ниже уровня Ферми.

Нейтронные подоболочки ядра ²⁰⁸Pb и нижние состояния ядер ²⁰⁷Pb и  ²⁰⁹Pb. Слева от уровня указана его энергия в МэВ. Показано количество нейтронов, заполняющих в основном состоянии внешние подоболочки ядра ²⁰⁸Pb.

    По мере заполнения внешней оболочки начинают проявляться коллективные эффекты.

Форма атомных ядер может изменяться в зависимости от того, в каком возбужденном состоянии оно находится. Так, например, ядро ¹⁸⁶Pb в основном состоянии (0⁺) сферически симметрично, в первом возбужденном состоянии 0⁺ имеет форму сплюснутого эллипса, а в состояниях 0⁺ , 2⁺ , 4⁺ , 6⁺ форму вытянутого эллипсоида. Форма атомного ядра может отличаться от сферически симметричной также и в основном состоянии ядра, о чем свидетельствуют наблюдаемые электрические квадрупольные моменты ядер.

Наблюдаемые электрические квадрупольные моменты ядер Q

    Пока число нуклонов во внешней оболочке мало, их коллективное взаимодействие проявляется в том, что в ядрах происходят колебания около сферически равновесной формы, наблюдается характерный спектр возбужденных состояний, состоящий из состояний положительной четности J^P = 0⁺, 2⁺, 4⁺, описываемых возбуждением одного, двух … квадрупольных фононов J^P = 2⁺. Примером могут служить спектры возбужденных состояний изотопов ⁶²Ni и ¹¹⁸Sn.
    Увеличение числа нуклонов в незаполненной оболочке вызывает деформацию атомного ядра в основном состоянии. В простейшем случае атомные ядра имеют форму вытянутого эллипсоида Q₀ > 0 или сплюснутого эллипсоида Q₀ < 0, что проявляется в характерном вращательном спектре эллипсоидальных деформированных ядер

где I – спин ядра, J – момент инерции ядра. Спин возбужденных состояний ядра I имеет характерную последовательность I = 2, 4, 6, 8, 10... Примером могут служить вращательные состояния четно-четных деформированных изотопов ¹⁷⁸Hf и ²³⁴U. Низшие возбужденные состояния вращательных спектров ядер расположены наиболее низко по энергии и легко возбуждаются в реакции под действием тяжелых ионов.

Колебательные состояния четно-четных ядер

Вращательные состояния деформированных четно-четных ядер

Возбужденные состояния 2⁺

    Состояния J^P = 2⁺ в атомных ядрах возникают в результате

• квадрупольных колебаний сферического ядра,
• вращения эллипсоидального деформированного ядра,
• одночастичного перехода.

    В зависимости положения первого 2⁺ уровня от массового числа А отчётливо проявляются эффекты, обусловленные деформацией атомного ядра. Энергия первого 2⁺ уровня в деформированных ядрах имеет гораздо меньшие значения, чем энергия колебательного 2⁺ уровня. В ядрах, имеющих заполненные оболочки, энергия 2⁺ уровня превышает 1 МэВ.
    Спектр возбуждённых состояний атомных ядер имеет сложную природу. Он является суперпозицией одночастичных возбуждений, коллек­тивных вращательных и колебательных возбуждений. Лишь в очень ограни­ченном числе ядер доминирует какая-либо одна из вышеперечисленных ветвей возбуждений. Характерные энергии одночастичных возбуждений в ядрах – мегаэлектронвольты, вибрационных – сотни - тысячи килоэлектронвольт, вращательных – десятки - сотни килоэлектронвольт.
    Модель ядерных оболочек столкнулась с проблемами при описании электрических квадрупольных моментов ядер. В модели ядерных оболочек оказалось невозможно объяснить большие квадрупольные моменты ядер, далеких от магических ядер, в частности, в ядрах с A = 140-190 и в области трансурановых элементов. Для описания таких ядер Дж. Рейнуотер предложил изменить одночастичную модель, основанную на сферически симметричном потенциале, и учесть деформацию, вызванную нуклонами внешней незаполненной оболочки. В коллективной модели, развитой Дж. Рейнуотером, О. Бором, Б. Моттельсоном, Б. Нильсоном, исходят из деформированного среднего эллипсоидального ядерного потенциала.

    Дж.Рейнуотер: «В модели оболочек Майер использует оболочечные волновые функции, основанные на сферическом потенциале. Работа Бора и Уиллера о делении показала, что ядра могут принимать сфероидальную форму, если это энергетически выгодно. Для малых значений отклонений β (разность большой и малой осей, отнесенной к среднему радиусу ядра) при постоянном объеме ядра поверхностная энергия возрастает как β², при этом некоторая компенсация происходит за счет уменьшения кулоновской энергии (для больших Z). Моя модель предполагала постоянную глубину ямы, при искажении ее формы: в направлении оси Z радиус R возрастает до (1 + 2β/3)R₀ и уменьшается по X и Y до (1 – 2β/3)R₀  (или соответственно R₀e^2β/3 и R₀e^-2β/3) … Многие ядра весьма значительно отклоняются от сферической формы и поэтому для этих областей не имеет смысла использовать сферическую модель ядра».

    Модель, развитая О. Бором, включает в себя, на первый взгляд, две противоположные модели – капельную и оболочечную. Остов атомного ядра рассматривается как деформированная жидкая капля, в которой возможны различные типы коллективных движений – вращения, колебания. Внешние нуклоны описываются так же как в модели оболочек. Благодаря связи движения внешнего нуклона и изменению поверхности атомного ядра полный момент ядра складывается из проекции спина нуклона на ось симметрии ядра и коллективного момента остова ядра. В этом случае полный момент нуклона перестает быть хорошим квантовым числом. Энергия состояния нуклона в деформированном эллипсоидальном потенциале зависит от проекции момента на ось симметрии ядра.

    О.Бор: «Джеймс Рейнуотер думал о происхождении больших квадрупольных моментов и высказал идею, которая сыграла решающую роль в развитии теории. Он осознал, что если учесть деформированность ядра как целого, то прямым следствием одночастичного движения по анизотропным орбитам будет возникновение несферической равновесной формы… Оказалось, что схема связи, характеризующая сильно деформированные ядра с четко выраженной полосой вращательных состояний реализуется для обширного класса ядер. Кульминацией волнующей весны 1953 г. стало открытие процесса кулоновского возбуждения, представившего возможность систематического изучения вращательных возбуждений».

    Многие свойства атомных ядер зависят от деформации ядра, которая в свою очередь зависит от конфигурации нуклонов внешней оболочки. В области заполненных оболочек ядра имеют равновесную сферическую форму и в таких ядрах наблюдаются как одначастичные степени возбуждения, так и колебания сферически симметричного остова. Вдали от заполненных оболочек ядра приобретают большую деформацию. В этом случае также можно выделить одночастичные возбуждения нуклонов относительно деформированного остова и вращательное состояние деформированного остова.
    Разделение возбуждений в ядре на одночастичное и коллективное соответствует предположению, что в общем случае волновая функция Ψ, являющаяся решением уравнения Шредингера для ядра, имеет вид

Ψ = Ψ_{одночаст}Ψ_колебΨ_вращат,

Ψ_{одночаст}   соответствует одночастичному возбуждению,

Ψ_колеб  соответствует колебанию ядра относительно своей равновесной формы,

Ψ_вращат   соответствует коллективному вращательному движению ядра как целого.

    Б. Моттельсон: «Картина ядерной динамики включает большое разнообразие различных коллективных возбуждений, которые настолько элементарны как и сами одночастичные возбуждения, в том смысле, что они остаются приблизительно независимыми при конструировании ядерного спектра возбуждений … Центральным элементом в анализе элементарных видов возбуждений и их взаимодействий является связь частицы с колебаниями, которая выражает вариации среднего потенциала, связанные с коллективной колебательной амплитудой. Эта связь представляет собой организующий элемент, который генерирует самосогласованные коллективные типы возбуждений из возбуждений частиц. В то же время она приводит к взаимодействиям, которые дают естественный предел для анализа в терминах элементарных видов возбуждений».

Обобщенная модель ядра

Джеймс Рейнуотер (1917-1986)

Оге Бор (1922-2009)

Бен Моттельсон (р. 1926)

    В простейшем варианте обобщенной модели ядер учитываются два типа ядерных движений: коллективное вращение ядра относительно внешней системы координат (x,y,z), обусловленное его деформацией, и одночастичное движение нуклонов относительно внутренней, вращающейся системы координат (1, 2, 3) в деформированной потенциальной яме.
J' − момент количества движения нуклона,
R − вращательный момент количества движения остова ядра,
J − полный момент количества движения (спин) ядра,
ћK − проекция спина ядра на ось симметрии ядра.

Нобелевская премия по физике
1975 г. − О. Бор, Б. Моттельсон и Дж. Рейнуотер
За открытие связи между коллективным и одночастичным движением в атомном ядре и создание на базе этой теории структуры атомного ядра.

Как возникла модель сфероидальных ядер
Дж. Рейнуотер

    В первой половине 1949 г. три группы в одном и том же выпуске «Physical Review» представили различные «объяснения» оболочечной структуры ядра. Из них работа Марии Майер представляет принятую теперь, модель. Похожее предложение И. Г. Д. Иенсена с сотрудниками было опубликовано в то же время. За эти работы Майер и Иенсену была присуждена Нобелевская премия по физике в 1963 г.
    Я был весьма заинтересован моделью оболочек, предложенной Майер, поскольку эта модель неожиданно позволила понять большое количество экспериментальных данных о спинах, о магнитных моментах изомерных состояний, о систематике β-распада и «магические числа» при Z, N = 2, 8, 20 (28), 50, 82, 126.
    Наблюдается качественное согласие, с моделью «оболочек Майер – Иенсена, значения моментов проходят через нуль при заполнении нейтронных и протонных оболочек. Для ядер с заполнённой оболочкой плюс один протон с очень высоким значением орбитального момента квадрупольные моменты отрицательны, как и ожидалось, так как протон располагается на экваториальной орбите. При удалении нуклонов из заполненных оболочек с высоким значением l значение Q возрастает и становится положительным, достигая максимального значения при заполнении орбиты с данным l почти наполовину и убывая при дальнейшем уменьшении числа нуклонов. Проблема заключалась в том, что значение Q/R² при R=1,5·10^–12 см достигает 10 для ядра ¹⁷⁶Lu, что в 30 раз превышает значение, которое можно было бы ожидать на основе волновых функций для сферического потенциала модели оболочек, связанных таким образом, чтобы дать состояние 7^– (Z = 71, N = 105, τ = 4·10¹⁰ лет). Для ядер редкоземельной области наиболее часто встречаются значения Q, сильно превышающие ожидаемые величины.
    Одним из интересныx свойств, даваемых моделью оболочек для деформированного ядра, является возможность прохождения внутренней энергии через минимум при возрастании деформации. Затем внутренняя энергия возрастает, пока энергия орбиты, вначале расположенной при большей энергии, но убывающей быстрее с деформацией, не пересечет последнюю заполненную вначале орбиту и не станет определять наименее связанное заполненное состояние.

Вращательное движение в ядрах
О. Бор

    Трудно сегодня полностью представить то потрясение, которое испытали физики, воспитанные на представлениях модели жидкой капли и модели составного ядра, на которых основывалась интерпретация ядерных явлений в течение предыдущего десятилетия, в связи с обнаружением оболочечной структуры ядра.
    Значение магнитных моментов в то время представлял собой один из наиболее обширных количественных классов данных по свойствам ядер. Эти данные требовали разъяснения от теории. Значения моментов обнаруживали сильную корреляцию с предсказаниями одночастичной модели, однако вместе с тем наблюдались существенные отклонения, которые свидетельствовали о наличии некоторого не включенного в рассмотрение эффекта.
    Ключ к пониманию отклонений схемы связи угловых моментов в ядре от предсказаний одночастичной модели дало обнаружение у многих ядер большого квадрупольного момента, более чем на порядок превышающего одночастичные значения. Из этого факта непосредственно следовало распределение углового момента между многими частицами, что, казалось, подразумевало нарушение применимости одночастичной модели. Однако основные черты одночастичной модели могут быть сохранены, если предположить, наличие отклонения от сферической симметрии у среднего ядерного поля, в котором движется нуклон. Такая картина приводит к модели ядра, напоминающей модель молекулы. В этой модели сердцевина ядра обладает колебательными и вращательными степенями свободы. По-видимому, нет никакого основания ожидать, что вращательное движение является классическим движением твердого тела. Однако вследствие большого числа нуклонов, участвующих в образовании деформащш, частота вращения должна быть мала по сравнению с частотой движения отдельных частиц.
    В этот момент существенной поддержкой для обсуждаемых работ явилось следующее открытие. Оказалось, что схема связи, характеризующая сильно деформированные ядра с четко выраженной полосой вращательных состояний, реализуется для обширного класса ядер. Первое указанно было получено Гольдхабер и Саньяром, которые обнаружили, что вероятности электрических квадрупольных переходов для распада низколежащих возбужденных состояний в четно-четных ядрах в ряде случаев были значительно больше соответствующих значений для одночастичных переходов. Это свидетельствовало о наличии коллективных видов возбуждения. Вскоре стали накапливаться указания на то, что рассматриваемые возбуждения являются частью последовательности уровней с угловыми моментами I = 0, 2, 4… и энергиями, пропорциональными I (I + 1).

Элементарные виды возбуждения в ядрах
Б. Моттелъсон

    Когда я впервые приехал в Копенгаген в 1950 г., было известно, что в ядрах иногда имели место явления, обусловленные независимым движением частиц, тогда как в других явлениях, например, в процессе деления и в проблеме больших квадрупольных моментов, несомненно, проявлялось коллективное поведение всего ядра как целого.
    Большой класс спектров имеет черты, соответствующие квадрупольным колебаниям относительно сферически симметричной формы. Существование статической деформации в некоторых классах ядер получило дальнейшее решающее подтверждение в успешной классификации соответствующих состояний этих спектров в терминах одночастичного движения и надлежащим образом деформированном потенциале.
    Замечательной особенностью развивающейся картины ядерных спектров возбуждения было разделение на классы ядер сферической формы и ядер с большими деформациями.
    В то время как в образовании низкочастотных спектров доминируют переходы частиц внутри частично заполненных оболочек, с возбуждением замкнутых оболочек связаны новые виды ядерной динамики. Классическим примером коллективного возбуждения этого типа является «гигантский дипольный резонанс».
    Центральным элементом в анализе элементарных видов возбуждения и их взаимодействий является связь частицы с колебанием, которая выражает вариации среднего потенциала, связанные с коллективной колебательной амплитудой. Эта связь представляет собой организующий элемент, который генерирует самосогласованные коллективные типы возбуждений из возбуждений частиц. В то же время она приводит к взаимодействиям, которые дают естественный предел для анализа в терминах элементарных видов возбуждения.

Одночастичные состояния деформированных ядер

Энергетические уровни ядра ²⁴⁹Bk. Слева изображены все наблюдаемые уровни в энергетическом интервале 0-600 КэВ. Справа приведено разбиение этих уровней на три вращательных полосы.

Энергетические уровни ядра ¹⁶⁸Er. Под каждой вращательной полосой указаны проекция K углового момента на ось симметрии и четность π. Сверху над каждым вращательным уровнем указаны спин J и энергия возбуждения E соответствующего состояния. Уровень энергии 821.19 кэВ отвечает квадрупольным колебаниям деформированной ядерной поверхности.

    Дипольный гигантский резонанс атомных ядер. Яркий пример образования коллективной степени свободы из одночастичных переходов – электрический гигантский дипольный резонанс в атомных ядрах.
    Возбуждение ядерного кора проявляется при более высоких энергиях. Так, во всех ядрах наблюдается дипольный гигантский резонанс, который расположен в районе 25 МэВ в легких ядрах и при 12–15 МэВ – в тяжелых ядрах. Простейшая интерпретация дипольного гигантского резонанса – колебание всех протонов относительно всех нейтронов. Такие колебания возбуждаются в реакциях под действием γ-квантов.
    Одночастичные возбуждения, возникающие как результат перехода нуклона между соседними оболочками в результате частично-дырочного взаимодействия приводят к формированию коллективного состояния, вбирающего в себя всю силу одночастичных переходов и сдвинутого к более высокой энергии по сравнению с одночастичными переходами. В рамках коллективных моделей такое коллективное состояние интерпретируется как когерентные дипольные колебания протонов относительно нейтронов. Коллективизация состояний дипольного гигантского резонанса приводит к уменьшению его энергетической области возбуждения. По мере увеличения массового числа A положение максимума гигантского резонанса смещается к меньшим энергиям от 25 МэВ в лёгких ядрах к 12 МэВ в тяжёлых ядрах. Положением максимума гигантского резонанса E хорошо аппроксимируется соотношением

E = 78A^-1/3 МэВ.

Интегральное сечение поглощения в области гигантского резонанса σ описывается соотношением

σ = 60NZ/A МэВ×мбн.

    В области деформированных ядер гигантский резонанс расщепляется на две компоненты, соответствующие колебаниям протонов относительно нейтронов вдоль двух осей ядерного эллипсоида (¹⁵⁹Tb, ²³⁵U). В лёгких ядрах (⁶Li, ¹⁶O, ³²S) проявляется конфигурационное расщепление дипольного гигантского резонанса, соответствующее дипольным переходам нуклонов из различных оболочек. В лёгких ядрах эффекты коллективизации ещё не проявляются столь сильно, как в тяжёлых ядрах, в которых значительно увеличивается число коллективизированных одночастичных переходов.

Дипольный гигантский резонанс атомных ядер

Кластеры в лёгких ядрах

    Несмотря на то, что в простейших моделях атомное ядро обычно рассматривается как система, состоящая из отдельных нуклонов, в результате взаимодействия между нуклонами в ядре образуются компактные структуры, состоящие из двух или большего числа частиц, которые могут возникать внутри атомного ядра. Кластерная структура особенно отчетливо проявляется в лёгких ядрах. Кластерная структура атомных ядер проявляется в процессах α-распада, в различных ядерных реакциях.