Радиоактивностью называется способность атомного ядра самопроизвольно распадаться с испусканием частиц.
    Радиоактивный распад ядра возможен тогда, когда он энергетически выгоден, т.е. сопровождается выделением энергии. Условием этого является превышение массы M исходного ядра суммы масс m_i продуктов распада, которому соответствует неравенство M > ∑m_i. Это условие является необходимым, но не всегда достаточным. Распад может быть запрещен другими законами сохранения – сохранения момента количества движения, электрического заряда, барионного заряда и т.д.
    Радиоактивный распад характеризуется временем жизни радиоактивного изотопа, типом испускаемых частиц, их энергиями.
    Основными видами радиоактивного распада являются:

• α-распад – испускание атомным ядром α-частицы;
• β-распад – испускание атомным ядром электрона и антинейтрино, позитрона и нейтрино, поглощение ядром атомного электрона с испусканием нейтрино;
• γ-распад – испускание атомным ядром γ-квантов;

• спонтанное деление – распад атомного ядра на два осколка сравнимой массы.

    К более редким видам радиоактивного распада относятся процессы испускания ядром двух электронов, одного или двух протонов, а также кластеров – лёгких ядер от   ¹²C  до  ³²S.   Во  всех  видах  радиоактивности   (кроме γ-распада) изменяется состав ядра – число протонов Z, массовое
число A или и то и другое одновременно.
    На характеристики радиоактивного распада существенное влияние оказывает тип взаимодействия, вызывающего распад ядра.
    Для того чтобы происходил α-распад, необходимо, чтобы масса исходного ядра M(A,Z) была больше суммы масс конечного ядра M(A-4, Z-2) и α-частицы m_α:

M(A,Z) > M(A-4, Z-2) + m_α.

    Энергия α-распада

Q_α = [M(A,Z) - M(A-4, Z-2) - m_α]c².

    Энергия, освобождающаяся при α-распаде, обычно заключена в интервале 2 – 9 МэВ, и основная её часть (» 98%) уносится α‑частицей в виде её кинетической энергии. Оставшиеся 2% - это кинетическая энергия конечного ядра. Периоды полураспада α-излучателей изменяются в очень широких пределах: от 5·10^-8 с до 8·10¹⁸ лет. Столь широкий разброс периодов полураспада, а также огромные значения этих периодов для многих α-радиоактивных ядер объясняется тем, что α-частица не может «мгновенно» покинуть ядро, несмотря на то, что это энергетически выгодно. Для того чтобы покинуть ядро, α-частица должна преодолеть потенциальный барьер (рис. 11).

    Главной особенностью β-распада является то, что он обусловлен слабым взаимодействием. Бета-распад - процесс внутринуклонный. В ядре распадается одиночный нуклон. Происходящие при этом внутри ядра превращения нуклонов и энергетические условия соответствующего типа β‑распада выглядят так (масса ν_e, _e считается нулевой):

• β^--распад (n ® p + e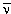^- + _e),      M(A,Z) > M(A, Z+1) + m_e,

• β⁺-распад (p ® n + e⁺ + ν_e),     M(A,Z) > M(A,Z-1) + m_e,

• e-захват (p + e^- ® n + ν_e),      M(A,Z) + m_e > M(A, Z-1).

При e-захвате ядро поглощает один из электронов атомной оболочки (обычно из ближайшей к нему K-оболочки), испуская нейтрино.

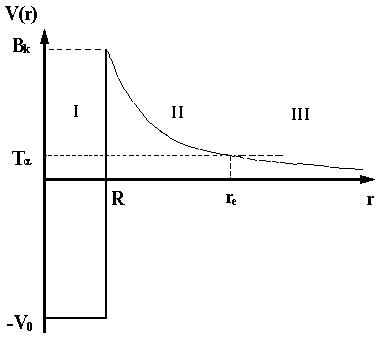Рис. 11. Потенциальная энергия α-частицы.

    Потенциальный барьер на границе ядра образуется за счет потенциальной энергии электростатического отталкивания α-частицы и конечного ядра и сил притяжения между нуклонами.
    Для четно-четных изотопов зависимость периода полураспада от энергии α-распада Q_α  хорошо описывается эмпирическим законом Гейгера-Неттола

lg T_1/2 = A + B/(Q_α)^1/2,

где A и B - константы слабо зависящие от Z.

   С учетом заряда дочернего ядра Z связь между периодом полураспада T_1/2 и энергией альфа-распада Q_α может быть представлено в виде (B.A. Brown, Phys. Rev. c46, 811 (1992))

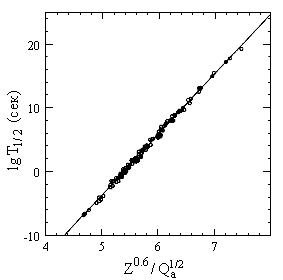
lg T_1/2 = 9.54Z^0.6/(Q_α)^1/2 - 51.37,

где период полураспада T_1/2 выражен в секундах, а Q_α - в МэВ.
  На рисунке показаны экспериментальные значения периодов полураспада для 119 альфа -радиоактивных четно-четных ядер (Z от 74 до 106) и их описание с помощью этого соотношения.
  Для нечетно-четных, четно-нечетных и нечетно-нечетных ядер общая тенденция сохраняется, но их периоды полураспада в 2 - 1000 раз больше, чем для четно-четных ядер с данными Z и Q_α.

     Если α-распад наблюдается только в случае самых тяжелых и некоторых редкоземельных ядер, то β‑радиоактивные ядра гораздо более многочисленны и имеются во всей области значений массового числа A, начиная от единицы (свободный нейтрон) и кончая массовыми числами самых тяжелых ядер. Для того чтобы выполнялись законы сохранения энергии и углового момента при распаде нуклона внутри ядра, последнее должно перестраиваться. Поэтому период полураспада, а также другие характеристики β‑распада зависят от того, насколько сложна эта перестройка. В результате периоды β‑распада варьируются почти в столь же широких пределах, как и периоды α-распада. Они лежат в интервале 10^-6 с - 10¹⁷ лет.
    Изменения состояний атомных ядер, сопровождающиеся    испусканием    или    поглощением    γ-квантов, называют γ-переходами. Периоды полураспада для γ-переходов изменяются от 10^-19 с до 10¹⁰ лет. Энергии γ-переходов изменяются от нескольких кэВ до нескольких МэВ.
    Полный момент количества движения фотона J называется мультипольностью фотона. Значение спина фотона J = 1, а поэтому, полный момент J, уносимый фотоном, может принимать целочисленные значения 1, 2, ... (кроме нуля).
    Различают электрические (EJ)  и магнитные (MJ) переходы. Е1 - электрический дипольный переход, М1 - магнитный дипольный переход, Е2 - электрический квадрупольный переход и т.д.
    Для электрических переходов четность определяется соотношением P = (–1)^J, для магнитных переходов — соотношением P = (–1)^J+1.
    В случае γ-переходов большой диапазон периодов полураспада объясняется сильной зависимостью вероятности γ-перехода от энергии и мультипольности переходов. Период полураспада T_1/2 γ-перехода зависит от мультипольности перехода J и приведенной длины волны излучения .

Для электрических переходов EJ –	,
для магнитных переходов MJ  –	,

где R - радиус ядра.

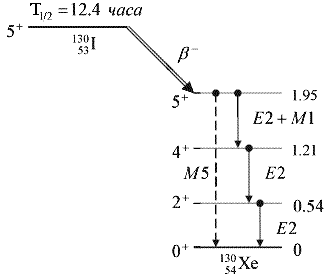Рис. 12. β- и γ-переходы в изотопах 130I и 130Xe.

    На рис. 12 приведена схема нижних уровней и γ‑переходов между ними в изотопах ¹³⁰I и ¹³⁰Xe. Уровни ядра ¹³⁰Xe заселяются в результате β^--распада основного состояния ядра ¹³⁰I, имеющего спин и четность J^P = 5⁺, на возбужденное состояние J^P = 5⁺ ядра ¹³⁰Xe с энергий 1.95 МэВ. При β^--распаде ядро ¹³⁰I превращается в ядро ¹³⁰Xe.
    В основном состоянии ядро ксенона имеет характеристики J^P = 0⁺. Поэтому распад на этот уровень является запрещенным β-переходом 4-го порядка и практически не происходит. Первый возбужденный уровень ядра ¹³⁰Xe с энергией 0.54 имеет характеристики J^P = 2⁺, а второй возбужденный уровень с энергией 1.21 МэВ - J^P = 4⁺. β-распады на них также подавлены, хотя и не так сильно, как распад на основное состояние.
    β^--распад на уровень ядра ¹³⁰Xe, имеющий энергию 1.95 МэВ и характеристики J^P = 5⁺, является разрешенным. Период полураспада изотопа ¹³⁰I равен 12.4 ч.
    Ядро ¹³⁰Xe, оказавшись в результате β^--распада ядра ¹³⁰I в состоянии с энергией 1.95 МэВ, может перейти в основное состояние очень большим числом способов, как в результате непосредственного перехода с испусканием γ‑кванта (показан пунктиром), так и в результате различных каскадов, например, каскада типа 5⁺ → 2⁺ → 0⁺, в котором первый переход имеет мультипольность M3, а второй – E2.
    Переход 5⁺ → 4⁺ может происходить в результате испускания Е2 и М1 γ-квантов.

    По мере удаления от долины β-стабильности происходит увеличение энергии β-распада и уменьшение энергии отделения нуклонов. Испускание запаздывающих частиц – двухстадийный процесс. На первой стадии происходит β-распад. При этом дочернее ядро может образоваться в возбужденном состоянии. На второй стадии происходит распад ядра из возбужденного состояния с испусканием нейтронов, протонов и более тяжелых фрагментов. Частицы, испускаемые в таком процессе, называются запаздывающими, так как период полураспада, наблюдаемый в результате регистрации нуклонов или фрагментов, будет определяться временем предшествующего β-распада. На рис. 13 показано испускание запаздывающих протонов ядром ²¹Mg.

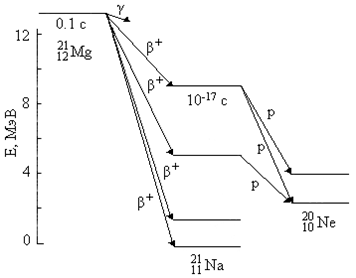Рис. 13. Испускание запаздывающих протонов ядром 21Mg.

    Ядро ²¹Mg нестабильно и в результате β⁺-распада превращается в изотоп ²¹Na:

²¹Mg  → ²¹Na + e⁺ + ν_e (T_1/2 = 0.12 c).

    В том случае, когда ядро ²¹Na образуется в состояниях с энергией меньше 2.5 МэВ, в нем происходят γ-переходы в основное состояние. Однако если энергия возбуждения ядра ²¹Na превышает 2.5 МэВ, открывается новая возможность. Ядро ²¹Na может, испустив протон, превратиться в устойчивый изотоп ²⁰Ne:

²¹Na → ²⁰Ne + p.

    Испускание протона происходит практически мгновенно, после β⁺-распада ядра ²¹Mg (T_1/2 около 10^-17 с), т. е. наблюдается практически одновременное появление протона и позитрона.

    Радиоактивный распад – статистический процесс. Каждое радиоактивное ядро может распасться в любой момент, и закономерности распада атомных ядер наблюдаются только в среднем, в случае распада достаточно большого количества ядер.
    Для характеристики скорости (вероятности) радиоактивного распада используются три взаимосвязанные величины − постоянная распада λ, среднее время жизни τ и период полураспада T_1/2.
    Постоянная распада λ − вероятность распада ядра в единицу времени. Если в образце в момент времени t имеется N радиоактивных ядер, то количество ядер dN, распавшихся за время dt, пропорционально N, λи интервалу времени наблюдений dt:

dN = –λNdt.

Знак «–» означает, что число радиоактивных ядер в образце в результате распада уменьшается.
    Закон радиоактивного распада имеет вид:

N(t) = N₀e^-λt,

    Среднее время жизни τ:

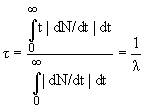
    Период полураспада T_1/2 – время, за которое первоначальное количество радиоактивных ядер уменьшается в два раза:

T_1/2 = ln2/λ=0.693/λ = ln2.

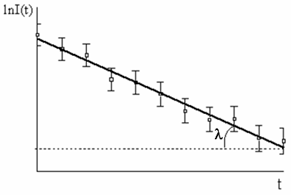Рис. 14. Определение постоянной распада.

    Постоянную распада λ определяют, измеряя зависимость числа распадов радиоактивного изотопа от времени. В тех случаях, когда период полураспада составляет от долей секунды до нескольких лет, для определения постоянной распада используется соотношение

lnI(t) = lnI(0) - λt.

Построив зависимость активности источника от времени в полулогарифмическом масштабе lnI(t) по углу наклона прямой к оси t, можно определить величину λ.