В процессах
взаимодействий и превращений частиц выполняются законы сохранения. Ряд законов
сохранения универсален, т. е. выполняется всегда, при всех типах
взаимодействий. Другие в некоторых взаимодействиях не выполняются. Как правило,
если существует сохраняющаяся физическая величина, ей соответствует определенная
инвариантность относительно операции симметрии.
К универсальным законам сохранения относятся законы,
которые обусловлены инвариантностью уравнений движения относительно
трансляций в пространстве и во времени. С этими типами симметрий – однородностью
пространства и времени – связано существование законов сохранения импульса и
энергии изолированных систем частиц. Изотропность трёхмерного пространства, т.
е. инвариантность уравнений движения относительно вращений, приводит к закону
сохранения момента количества движения.
Если преобразование волновой функции, отвечающее закону
сохранения, имеет непрерывный характер, то соответствующий закон сохранения
аддитивен, т.е. в реакции
a + b → c + d +...
сохраняется сумма соответствующих квантовых чисел:
Na + Nb = Nc + Nd +... = const.
Трансляции и повороты – непрерывные преобразования и соответствующие законы сохранения (энергии, импульса и момента количества движения) – аддитивны. Аддитивными сохраняющимися величинами являются также электрический заряд Q, барионное квантовое число (барионный заряд) B, лептонные квантовые числа (лептонные заряды) Le, Lμ, Lτ, изоспин I, а также ряд других квантовых чисел, имеющих кварковую природу – странность s, очарование (charm) c, bottom b, top t.
 Эуген Вигнер (1902 – 1995) |
Принципы симметрии в физике
1927 г. Э. Вигнер сформулировал закон сохранения
пространственной четности.
1936 г. Э. Вигнер разработал теорию поглощения нейтронов
атомными ядрами.
Инвариантность в физической теории
Мир очень сложен и человеческий разум явно не в
состоянии полностью постичь его. Именно поэтому человек придумал искусственный
прием − в сложной природе мира винить то, что принято называть случайным, − и
таким образом смог выделить область, которую можно описать с помощью простых
закономерностей. Сложности получили называние начальных условий, а то, что
абстрагировано от случайного, − законов природы. Каким бы искусственным ни
казалось подобное разбиение структуры мира при самом беспристрастном подходе и
даже вопреки тому, что возможность его осуществления имеет свои пределы, лежащая
в основе такого разбиения абстракция принадлежит к числу наиболее плодотворных
идей, выдвинутых человеческим разумом. Именно она позволила создать естественные
науки.
Возможность абстрагирования законов движения из
хаотического множества происходящих вокруг нас явлений основывается на двух
обстоятельствах. Во-первых, во многих случаях удается выделить множество
начальных условий, которое не слишком велико, но в то же время содержит все, что
существенно для интересующих нас явлений. В классическом примере свободно
падающего тела можно пренебречь почти всеми условиями, кроме начального
положения и начальной скорости падающего тела: его поведение будет всегда одним
и тем же, независимо от степени освещенности, наличия вблизи от него других тел,
их температуры и т. д. Выделение множества условий, оказывающих влияние на тот
или иной эксперимент, отнюдь не является тривиальной задачей. Наоборот, умение
выделить такие условия и составляет основу искусства экспериментатора.
Нобелевская премия по физике
1963 г. − Э. Вигнер. За вклад в теорию атомного ядра и элементарных частиц, в частности за открытие и применение фундаментальных принципов симметрии.
Таблица 17.1
Законы сохранения
Характеристика |
Взаимодействие |
||
|---|---|---|---|
Сильное |
Электромагнитное |
Слабое |
|
Аддитивные законы сохранения |
|||
Электрический заряд, Q |
+ |
+ |
+ |
Энергия, E |
+ |
+ |
+ |
Импульс,
|
+ |
+ |
+ |
Момент количества движения,
|
+ |
+ |
+ |
Барионный заряд, B |
+ |
+ |
+ |
Лептонные заряды, Le, Lμ, Lτ |
+ |
+ |
+ |
Странность, s |
+ |
+ |
- |
Очарование (charm), c |
+ |
+ |
- |
Bottom, b |
+ |
+ |
- |
Top, t |
+ |
+ |
- |
Изоспин, I |
+ |
- |
- |
Проекция изоспина, I3 |
+ |
+ |
- |
Мультипликативные законы сохранения |
|||
|---|---|---|---|
Пространственная четность, P |
+ |
+ |
- |
Зарядовая четность, C |
+ |
+ |
- |
Инвариантность к обращению времени, T |
+ |
+ |
- |
Комбинированная четность, CP |
+ |
+ |
- |
CPT-инвариантность |
+ |
+ |
+ |
С какими типами симметрий связаны законы сохранения
квантовых чисел Q, B, Le, Lμ, Lτ, I,
s, c, b, t? В настоящее время известен ответ лишь
для электрического заряда Q и изоспина I. Сохранение изоспина в
сильных взаимодействиях – следствие инвариантности этого взаимодействия
относительно поворотов в изоспиновом пространстве. Сохранение
электрического заряда есть следствие того, что не существует способа измерить
абсолютное значение электрического потенциала и во всех соотношениях он является
относительной величиной.
Наиболее неясная ситуация с барионным В и
лептонными квантовыми числами Le, Lμ, Lτ. Эти числа
лежат в основе классификации частиц, однако нет серьёзных теоретических
предпосылок для их строгого сохранения. Более того, в теориях объединения
взаимодействий (теориях Великого объединения) законы сохранения
барионного и лептонных чисел считаются нарушенными. В настоящее время оба этих
закона сохранения выполняются в пределах точности проведённых измерений, т. е.
эти законы сохранения имеют статус эмпирических. Обнаруженное явление
осцилляции нейтрино − превращение нейтрино одного типа в другой указывает на то,
что квантовые числа Le, Lμ и Lτ по-видимому не сохраняются порознь и более
общим законом сохранения будет закон сохранения суммы лептонных зарядов
Le + Lμ + Lτ = Le' + Lμ' + Lτ'.
Если преобразование волновой функции, отвечающее закону сохранения, дискретно, то соответствующий закон сохранения мультипликативен, т. е. в реакции сохраняется произведение соответствующих характеристик (квантовых чисел)
Na×Nb = Nc×Nd ... = const.
Дискретными преобразованиями являются операции
пространственной инверсии
![]() , зарядового
сопряжения
, зарядового
сопряжения ![]() , комбинированного преобразования
, комбинированного преобразования
![]()
![]() , операция обращения
времени
, операция обращения
времени ![]() и
и
![]()
![]()
![]() ‑преобразование.
Инвариантность относительно дискретных преобразований приводит к соответствующим
квантовым числам. Так инвариантность относительно пространственной инверсии
приводит к квантовому числу чётность Р. Все взаимодействия, кроме
слабого, инвариантны относительно пространственной инверсии и для них справедлив
закон сохранения пространственной чётности. Ещё одно дискретное преобразование
− операция зарядового сопряжения
‑преобразование.
Инвариантность относительно дискретных преобразований приводит к соответствующим
квантовым числам. Так инвариантность относительно пространственной инверсии
приводит к квантовому числу чётность Р. Все взаимодействия, кроме
слабого, инвариантны относительно пространственной инверсии и для них справедлив
закон сохранения пространственной чётности. Ещё одно дискретное преобразование
− операция зарядового сопряжения
![]() , изменяющая знаки зарядов частиц.
С инвариантностью относительно этого преобразования связано квантовое число
зарядовой чётности С.
, изменяющая знаки зарядов частиц.
С инвариантностью относительно этого преобразования связано квантовое число
зарядовой чётности С.
В таблице 17.1 дан перечень законов сохранения с
указанием выполнения законов сохранения в различных взаимодействиях. Значок «+» показывает, что квантовое число (величина) сохраняется в данном
взаимодействии, т.е. данное взаимодействие инвариантно к рассматриваемому
преобразованию. В противном случае приводится значок «–».
Первые шесть законов сохранения, приведенных в
таблице 17.1, универсальны, т. е. выполняются во всех взаимодействиях. Изоспин
сохраняется только в сильном взаимодействии. Остальные аддитивные величины не
сохраняются в слабом взаимодействии. Не сохраняются в слабом взаимодействии и
все три типа чётности − пространственная Р, зарядовая С и
комбинированная СР.
![]()
![]()
![]() -преобразование, являющееся совместным
действием
-преобразование, являющееся совместным
действием ![]() -,
-,
![]() - и
- и
![]() -преобразований, основано на
фундаментальных принципах квантовой теории поля. В силу инвариантности системы
относительно
-преобразований, основано на
фундаментальных принципах квантовой теории поля. В силу инвариантности системы
относительно ![]()
![]()
![]() -преобразования,
если в природе происходит какой-либо процесс, с такой же вероятностью должен
происходить процесс, в котором частицы заменены на античастицы, проекции их
спинов имеют противоположный знак, а начальное и конечное состояния поменялись
местами. Из CPT‑инвариантности следует, что энергетически спектры и угловые
распределения продуктов распада частиц и античастиц должны быть одинаковыми,
массы частицы и античастицы должны быть равны, времена жизни одинаковы,
электрические заряды и магнитные моменты частицы равны по абсолютной величине и
могут различаться только знаком.
-преобразования,
если в природе происходит какой-либо процесс, с такой же вероятностью должен
происходить процесс, в котором частицы заменены на античастицы, проекции их
спинов имеют противоположный знак, а начальное и конечное состояния поменялись
местами. Из CPT‑инвариантности следует, что энергетически спектры и угловые
распределения продуктов распада частиц и античастиц должны быть одинаковыми,
массы частицы и античастицы должны быть равны, времена жизни одинаковы,
электрические заряды и магнитные моменты частицы равны по абсолютной величине и
могут различаться только знаком.
Чень-Ин Янг:«Существование законов симметрии находится в полном соответствии с нашим жизненным опытом. Понятия о простейших
симметриях – изотропности и однородности пространства – появились на заре
человеческого сознания.
Инвариантность законов механики при
переходе к равномерно движущейся системе координат (известная также как инвариантность
относительно преобразования Галилея) явилась примером первой лишенной простоты
симметрии. Эта симметрия является одним из исходных принципов ньютоновской
механики. Следствия, вытекающие из этого принципа симметрии, интенсивно
разрабатывались физиками в прошлом веке и привели к ряду важных результатов.
Хорошим примером из этой области служит теорема, гласящая, что в изотропном
твердом теле могут быть только два модуля упругости.
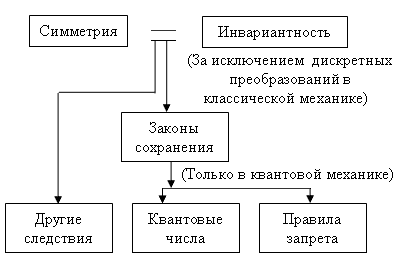
Соотношение между законами
сохранения и симметрией
Другого типа следствиями из законов
симметрии являются законы сохранения. В настоящее время общеизвестно, что,
вообще говоря, принцип симметрии (или, что то же самое, принцип
инвариантности) приводит к закону сохранения. Например, инвариантность
физических законов относительно пространственных трансляций приводит к закону
сохранения импульса, а инвариантность относительно пространственных вращений
приводит к сохранению момента. В то время как важность этих законов сохранения
была полностью понята, их тесная связь с законами симметрии не была полностью
установлена вплоть до начала
XX века.
В связи с созданием специальной и общей
теории относительности законы симметрии приобрели новое значение: между законами
симметрии и динамическими законами физика связь оказалась значительно более
тесной и взаимоопределяющей, чем в классической механике, где, по существу,
законы симметрии явились только следствиями динамических законов, случайно
обладавших симметрией. В релятивистской теории также было существенно расширено
число законов симметрии путем включения таких законов, которые на основе
обыденных представлений явились отнюдь не очевидными: скорее их справедливость
выводилась на основании сложных экспериментов (или в дальнейшем подтверждалась
сложными экспериментами).
Позвольте мне подчеркнуть, что для физиков
являлась могучим источником вдохновения идейная простота и внутренняя красота
симметрии, обнаруживаемой в сложных экспериментах. Появлялась надежда, что
природа таит в себе определенную упорядоченность, которую можно постигнуть.
Однако вплоть до появления квантовой
механики принципы симметрии были распространены в физике не очень широко.
Квантовые числа, которые определяют состояния системы, часто совпадают с
квантовыми числами, определяющими симметрию системы. Действительно, трудно
переоценить ту роль, которую играют принципы симметрии в квантовой механике.
Сошлемся на два примера: общее строение периодической системы элементов по
существу является прямым следствием изотропности закона Кулона; существование
античастиц – а именно позитрона, антипротона и антинейтрона – теоретически
предсказывалось как следствие инвариантности физических законов по отношению к
преобразованию Лоренца. В обоих случаях кажется, что природа использует
преимущество простоты математического представления законов симметрии. Чувство
глубочайшего уважения к мощи законов симметрии никогда не ослабевает у того, кто
обдумывал изящество и красоту безупречных математических доказательств и
сопоставлял это со сложными и далеко идущими физическими следствиями»[*].
Пространственная инверсия Р. Чётность
Операция пространственной инверсии P заключается в преобразовании
x, y, z,
![]() ,
,
![]()
![]() -x,
-y, -z, -
-x,
-y, -z, -![]() ,
,
![]() .
.
Операция P изменяет знак любого полярного вектора
![]()
![]() -
-![]() ,
,
![]()
![]() -
-![]() .
.
Аксиальные векторы при пространственной инверсии не изменяются
![]()
![]()
![]() .
.
Операция пространственной инверсии переводит систему в
зеркально симметричную. Зеркальная симметрия наблюдается в процессах под
действием сильного и электромагнитного взаимодействий. Зеркальная симметрия в
этих процессах означает, что в зеркально симметричных состояниях переходы
реализуются с одинаковой вероятностью. Это означает симметричность распадов
относительно плоскости перпендикулярной спину, т.е. угловые распределения
распадов поляризованных ядер симметричны под углами θ и (π − θ) относительно спина ядра.
Зеркальная симметрия гамильтониана взаимодействия не
исключает процессы, в которых зеркальная симметрия нарушена. Примером могут
служить некоторые молекулы, которые вращают плоскость поляризации света в
противоположные стороны. Это так называемое спонтанное нарушение симметрии.
Симметрия гамильтониана относительно зеркального отражения проявляется в том,
что наряду с левополяризующими молекулами существуют и правополяризующие
молекулы, являющиеся зеркальным отражением друг друга. Нарушение зеркальной
симметрии связано с вырождением основного состояния и распространением света в
среде, состоящей только из правополяризованных или левополяризованных молекул.
Инвариантность гамильтониана системы
![]() относительно
пространственного отражения – инверсии (замены
относительно
пространственного отражения – инверсии (замены
![]() → -
→ -![]() ) приводит к закону сохранения чётности и
квантовому числу чётность.
) приводит к закону сохранения чётности и
квантовому числу чётность.
Все свойства системы частиц определяются видом
гамильтониана ![]() и
волновой функции ψ(
и
волновой функции ψ(![]() ),
которая является решением соответствующего уравнения Шредингера. В приведенных
ниже соотношениях (17.1)–(17.23)
),
которая является решением соответствующего уравнения Шредингера. В приведенных
ниже соотношениях (17.1)–(17.23)
![]() обозначает совокупность координат всех
А
частиц, входящих в состав системы, т. е.
обозначает совокупность координат всех
А
частиц, входящих в состав системы, т. е.
![]() ≡
≡
![]() 1,
1,![]() 2,
...,
2,
...,![]() A.
A.
Инвариантность системы к пространственной инверсии
означает, что выполняется соотношение для плотности вероятности найти систему в
определенной точке многомерного пространства:
| |ψ( |
(17.1) |
В результате возникают два возможных преобразования волновой функции в результате пространственной инверсии:
| ψ(- |
(17.2) |
В первом случае волновая функция системы четная, во втором – нечётная. Соотношения (17.2) можно записать в виде одного равенства
ψ(-![]() )
= pψ(
)
= pψ(![]() ),
),
где
р = ±1 − квантовое
число чётность.
Квантовое число четность является собственным значением
оператора пространственной инверсии. Определим оператор пространственной
инверсии ![]() (оператор
чётности) для системы частиц следующим образом:
(оператор
чётности) для системы частиц следующим образом:
|
|
(17.3) |
Если подействовать на левую и правую части соотношения (17.3) ещё раз оператором
![]()
|
|
(17.4) |
получится исходное состояние системы, т. е.
![]() 2 − оператор тождественного
преобразования.
2 − оператор тождественного
преобразования.
Оператор ![]() , волновая функция ψ(
, волновая функция ψ(![]() ) и квантовое число четности р
в силу инвариантности системы относительно пространственного отражения должны
быть связаны уравнением на собственные значения
) и квантовое число четности р
в силу инвариантности системы относительно пространственного отражения должны
быть связаны уравнением на собственные значения
|
|
(17.5) |
Из (17.4) и (17.5) следует, что
![]() 2ψ(
2ψ(![]() )
= p2ψ(
)
= p2ψ(![]() )
= ψ(
)
= ψ(![]() ),
),
т.
е. p2
= 1 и собственные
значения оператора четности
![]() p = ±1.
p = ±1.
В результате получаем
|
|
(17.6) |
или
ψ(-![]() )
= ψ(
)
= ψ(![]() ) − чётные функции (состояния),
) − чётные функции (состояния),
ψ(-![]() ) = -ψ(
) = -ψ(![]() ) -нечётные функции (состояния).
) -нечётные функции (состояния).
В рассмотренном случае волновая функция ψ(![]() ) была волновой функцией
системы точечных (бесструктурных) частиц. В общем случае волновая функция
отдельной частицы имеет вид
) была волновой функцией
системы точечных (бесструктурных) частиц. В общем случае волновая функция
отдельной частицы имеет вид
| Ψ =
|
(17.7) |
где
![]() описывает внутреннее состояние частицы, а ψ(
описывает внутреннее состояние частицы, а ψ(![]() ) - перемещение частицы в пространстве как целого. Представление волновой
функции Ψ в форме (17.7) следует из того, что
гамильтониан частицы можно представить как сумму гамильтонианов
) - перемещение частицы в пространстве как целого. Представление волновой
функции Ψ в форме (17.7) следует из того, что
гамильтониан частицы можно представить как сумму гамильтонианов
![]() ψ +
ψ +
![]()
![]() , где
, где
![]() ψ описывает
бесструктурную частицу, а
ψ описывает
бесструктурную частицу, а
![]()
![]() -внутреннюю структуру частицы.
-внутреннюю структуру частицы.
Оператор чётности
![]() действует на каждый множитель волновой
функции Ψ =
действует на каждый множитель волновой
функции Ψ =
![]() ψ(
ψ(![]() ):
):
|
|
(17.8) |
Если ![]()
![]() -инвариантен относительно операции инверсии в пространстве внутренних
координат
-инвариантен относительно операции инверсии в пространстве внутренних
координат
![]() , то
, то
|
|
(17.9) |
где
π − внутренняя чётность
частицы.
Волновая функция ψ(![]() ) орбитального движения частицы в
центральном поле, т. е. движения с определённым орбитальным моментом
l,
может быть представлена в сферических координатах в виде разложения по
сферическим координатам
) орбитального движения частицы в
центральном поле, т. е. движения с определённым орбитальным моментом
l,
может быть представлена в сферических координатах в виде разложения по
сферическим координатам
| ψ( |
(17.10) |
Инверсия ![]() → -
→ -![]() соответствует в сферических координатах
преобразованию
соответствует в сферических координатах
преобразованию
r → r, θ → π − θ
(полярный угол),
φ →
π
+ φ (азимутальный угол),
при котором радиальная часть волновой функции Rnl(r) не изменяется, а Ylm(θ,φ) – собственная функция оператора орбитального момента количества движения (сферическая функция) – преобразуется следующим образом:
| Ylm(π-θ,φ+π) = (-1)lYlm(θ,φ). | (17.11) |
В результате получим
|
|
(17.12) |
Величина (-1)l называется
орбитальной чётностью.
Волновую функцию системы А независимых частиц
можно представить в виде произведения волновых функций отдельных частиц (в более
общем случае, в виде линейной комбинации этих произведений):
| ψ(1,2,...,A) = Ψ1·Ψ2·...ΨA, | (17.13) |
где
Ψ1 =
![]() 1ψ(
1ψ(![]() 1), Ψ2
=
1), Ψ2
= ![]() 2ψ(
2ψ(![]() 2), …, ΨA
=
2), …, ΨA
= ![]() Aψ(
Aψ(![]() A). Таким образом, при
движении частиц в центральном поле,
A). Таким образом, при
движении частиц в центральном поле,
![]() ψ(1,2,...,A) = π1π2...πA
ψ(1,2,...,A) = π1π2...πA![]() ψ(1,2,...,A),
ψ(1,2,...,A),
полная чётностьсистемы определяется четностью каждой частиц πi и её орбитальным моментом l.
|
|
(17.14) |
Для двух частиц
|
|
(17.15) |
где
L =
l1 + l2 –
орбитальный момент относительного движения частиц в системе их центра инерции.
Формулы (17.14), (17.15) можно применять к реакциям с частицами,
когда частицы до и после столкновения можно считать невзаимодействующими, а
также к ядру как системе нуклонов, рассматривая их как независимые частицы,
находящиеся в общем ядерном потенциале.
Ядерный гамильтониан
 |
(17.16) |
где

V(|![]() α
-
α
- ![]() β|) –
потенциал взаимодействия нуклонов
a и b, обладает инвариантностью к пространственной инверсии.
β|) –
потенциал взаимодействия нуклонов
a и b, обладает инвариантностью к пространственной инверсии.
Инвариантность гамильтониана относительно
пространственной инверсии (17.16) означает, что атомное ядро не изменяет своих
свойств при ![]() → -
→ -![]() и
ядерные состояния можно характеризовать определенной четностью, которая в
ядерных взаимодействиях сохраняется.
и
ядерные состояния можно характеризовать определенной четностью, которая в
ядерных взаимодействиях сохраняется.
Электромагнитные процессы также инвариантны
относительно пространственной инверсии, и четность в них сохраняется. Это
следует из того, что уравнения Максвелла не изменяются при преобразовании
![]() → -
→ -![]() . В отличие от сильных и
электромагнитных взаимодействий гамильтониан слабого взаимодействия не обладает
инвариантностью относительно зеркального преобразования
. В отличие от сильных и
электромагнитных взаимодействий гамильтониан слабого взаимодействия не обладает
инвариантностью относительно зеркального преобразования
![]() → -
→ -![]() . Это означает, что в слабых
взаимодействиях четность не сохраняется. Системы, в которых слабые
силы играют большую роль, нельзя характеризовать определенной четностью.
. Это означает, что в слабых
взаимодействиях четность не сохраняется. Системы, в которых слабые
силы играют большую роль, нельзя характеризовать определенной четностью.
Смысл имеют лишь относительные внутренние чётности. Для
протона, состоящего из трех кварков с положительной внутренней четностью и
нулевыми относительными орбитальными моментами, естественно получаем внутреннюю
чётность π(p) = +1.
Нейтроны также имеют внутреннюю чётность π(n) = +1. Внутренние чётности частиц определяют,
исходя из их кваркового состава и орбитального момента l кварков в составе адрона.
Соотношение
![]() ψ(
ψ(![]() )
= ψ(-
)
= ψ(-![]() )
)
справедливо для скалярных функций ψ(![]() ). При действии оператора
). При действии оператора
![]() на векторную функцию
на векторную функцию
![]() (
(![]() ) следует изменить не
только знаки радиусов-векторов частиц (
) следует изменить не
только знаки радиусов-векторов частиц (![]() → -
→ -![]() ), но также и знаки всех трёх компонент
вектора
), но также и знаки всех трёх компонент
вектора ![]() (Ax →
-Ax, Ay → -Ay, Az → -Az), что происходит при изменении направления
всех координатных осей на противоположные. Поэтому для любого истинного
(полярного) вектора имеет место соотношение
(Ax →
-Ax, Ay → -Ay, Az → -Az), что происходит при изменении направления
всех координатных осей на противоположные. Поэтому для любого истинного
(полярного) вектора имеет место соотношение
![]()
![]() (
(![]() )
= -
)
= -![]() (-
(-![]() ).
).
Для фотона внутренняя четность отрицательна π(γ) = -1. Это является
следствием того, что электромагнитное поле векторное. Оно описывается векторным
потенциалом ![]() ,
который эквивалентен волновой функции фотона, а для векторной функции
,
который эквивалентен волновой функции фотона, а для векторной функции
|
|
(17.17) |
что
позволяет приписать фотону π(γ) = -1.
Внутренние чётности частиц и античастиц с полуцелым
спином (фермионов) противоположны, с целым спином (бозонов) – одинаковы.
Внутренние чётности частиц определяют из распадов и
реакций с участием частиц с известной внутренней чётностью на
основе закона сохранения полной чётности.
В. Вайспопф,
Л. Родберг: «Новые недавно выполненные в ядерной физике опыты
свидетельствуют о том, что некоторые основные свойства природы имеют далеко не
тот характер, который им приписывали. В истории физики редко случалось, чтобы
изменение основных принципов следовало из результатов всего лишь нескольких
опытов.
Прежде чем обсудить сами опыты, мы
рассмотрим основной закон, ли который посягают полученные результаты. Это закон
четности. Он может быть выражен в следующей форме: каждый процесс, происходящий
в природе, может протекать и так, каким он виден отраженным в зеркале. Это
значит, что природа зеркально симметрична. Зеркальное изображение любого объекта
есть также возможный объект природы; движение любого объекта, рассматриваемого в
зеркале, есть также движение, разрешаемое законами природы. Любой выполненный в
лаборатории опыт может быть выполнен таким образом, каким он кажется в зеркале,
и любой полученный при этом эффект должен быть зеркальным изображением
действительного эффекта. Выражаясь кратко, законы природы инвариантны
относительно отражения.
Опыт был выполнен в Государственном Бюро
стандартов в Вашингтоне, где имеется криогенная техника для опытов при очень
низких температурах. Опыт осуществили
By из Колумбийского университета и Амблер, Хейворд, Хоппс и
Хадеон из Государственного Бюро стандартов. Они ориентировали вращение ядер
кобальта и сравнили электронные интенсивности в двух противоположных
относительно оси вращения направлениях.
Этот опыт имеет несколько замечательных
особенностей. Он принадлежит к тем опытам, произвести которые отважились бы
немногие физики, ибо его результат «с очевидностью» следовал из зеркальной
симметрии. Большие открытия всегда связаны с тем, что «очевидное» подвергается
сомнению. В этом случае заслуга принадлежит двум физикам теоретикам –
Ли из Колумбийского университета и Янгу из Института
проблемных исследований, которые указали экспериментаторам на необходимость
этого опыта. Ли и Янг предположили, что для некоторых слабых взаимодействий,
подобных β-распаду, принцип четности может оказаться неверным»[†].
Несохранение пространственной четности в слабых взаимодействиях
1956 г. Янг Чжэньнин, Ли Цзундао предположили нарушение
пространственной четности в слабых взаимодействиях.
1956 г. Ву Дзяньсюн открыла несохранение пространственной
четности в бета-распаде.
| Пространственная чётность P Пространственная чётность сохраняется в сильных и электромагнитных взаимодействиях и не сохраняется в слабых взаимодействиях. |
Нобелевская премия по физике
1957 г. − Янг Чжэньнин, Ли Цзундао. За глубокие исследования так называемых законов четности, которые привели к важным открытиям в области элементарных частиц.
 Янг Чжэньнин (р. 1922) |
 |
 Ли Цзундао (р. 1926) |
Зарядовая чётность
Операция ![]() зарядового сопряжения − это
операция замены знаков всех зарядов на противоположные
зарядового сопряжения − это
операция замены знаков всех зарядов на противоположные
x, y, z,
|
|
x, y, z,
|
При
этом пространственные координаты x, y, z,, импульс
![]() и спин
и спин
![]() частицы не изменяются. Так, например, в
случае барионов и лептонов изменение знака электрического заряда сопровождается
изменением знаков барионного B и лептонных Le, Lμ и
Lτ зарядов и, как следствие, изменением знака
магнитного момента
частицы не изменяются. Так, например, в
случае барионов и лептонов изменение знака электрического заряда сопровождается
изменением знаков барионного B и лептонных Le, Lμ и
Lτ зарядов и, как следствие, изменением знака
магнитного момента
![]() . Абсолютная величина магнитного момента не
изменяется.
. Абсолютная величина магнитного момента не
изменяется.
| Электрический заряд Q | |
| Барионный заряд B | |
| Лептонные заряды Le, Lμ, Lτ | |
| Спин J | |
| Магнитный момент | |
| Квантовые числа s,c,b,t |
Знаком перед магнитным моментом обозначен магнитный
момент параллельный и антипараллельный вектору спина, т.е. спиральность частицы.
Операция зарядового сопряжения переводит частицу в
античастицу и наоборот.
| (17.18) |
Это
утверждение несправедливо для нейтрино − частиц, имеющих определённое значение
спиральности[‡].
Если операцию зарядового сопряжения применить дважды,
то получится частица с исходными квантовыми числами:
| (17.19) |
Оператор ![]() 2 это оператор тождественного
преобразования, имеющий собственные значения c = ±1. Действительно, уравнение на собственные
значения имеет вид
2 это оператор тождественного
преобразования, имеющий собственные значения c = ±1. Действительно, уравнение на собственные
значения имеет вид
| (17.20) |
Отсюда, рассматривая совместно (17.19) и (17.20),
получаем c = 1 и
c = ±1. Однако оператор ![]() далеко не всегда имеет
собственные значения, т. е. не для всех частиц или систем частиц формально
записанное соотношение (17.20) имеет физический смысл. Если подействовать
оператором зарядового сопряжения
далеко не всегда имеет
собственные значения, т. е. не для всех частиц или систем частиц формально
записанное соотношение (17.20) имеет физический смысл. Если подействовать
оператором зарядового сопряжения ![]() на состояние |π+>, описывающее π+-мезон:
на состояние |π+>, описывающее π+-мезон:
| (17.21) |
Получаем состояние |π->,
отличное от исходного состояния |π+>. Поэтому для π±-мезона невозможно
выполнение уравнения (17.20). Это свойство оператора ![]() обусловлено тем, что он не коммутирует с
оператором заряда.
обусловлено тем, что он не коммутирует с
оператором заряда.
Оператор зарядового сопряжения имеет собственные
значения только для полностью нейтральных (истинно нейтральных) частиц, таких
как фотон γ, нейтральные мезоны qiqi −
π0, η, η', ρ,![]() , ω и другие, а также для
полностью нейтральных систем частиц π+π-, e+e- и др. Для таких частиц (систем)
соотношение (17.20) приобретает смысл и величина C, называемая
зарядовой чётностью, равна либо +1, либо -1. Зарядовая чётность с является мультипликативным квантовым
числом.
, ω и другие, а также для
полностью нейтральных систем частиц π+π-, e+e- и др. Для таких частиц (систем)
соотношение (17.20) приобретает смысл и величина C, называемая
зарядовой чётностью, равна либо +1, либо -1. Зарядовая чётность с является мультипликативным квантовым
числом.
Как приписать определённое значение
зарядовой чётности истинно нейтральным частицам? Квант электромагнитного поля – фотон – описывается векторным потенциалом ![]() (
(![]() ,t), который создается
электрическими зарядами. При зарядовом сопряжении все заряды изменяют знаки, а
значит, изменяет знак и создаваемый ими векторный потенциал
,t), который создается
электрическими зарядами. При зарядовом сопряжении все заряды изменяют знаки, а
значит, изменяет знак и создаваемый ими векторный потенциал ![]() . Поэтому, обозначая состояние
фотона |γ> = |
. Поэтому, обозначая состояние
фотона |γ> = |![]() >,
можно записать
>,
можно записать
| (17.22) |
Таким образом, зарядовая чётность фотона отрицательная
C(γ) = -1.
Используя то обстоятельство, что электромагнитное взаимодействие С-инвариантно и зарядовая чётность в этом взаимодействии сохраняется, можно приписать определённую зарядовую чётность π0-мезону. Так как π0 распадается в результате электромагнитного взаимодействия на два фотона: π0→2γ, то он должен иметь положительную зарядовую чётность:
| (17.23) |
Таким образом, зарядовая чётность π0 положительна
C(π0) = +1.
Сохранение зарядовой чётности запрещает некоторые
распады. Так, например, распад π0→3γ за счёт электромагнитного взаимодействия невозможен, т.к. зарядовая
чётность π0-мезона
+1, в то время как зарядовая чётность трёх γ-квантов (-1)(-1)(-1) =-1.
Получим общее выражение для зарядовой чётности системы
фермион-антифермион (позитроний e+e- или q![]() ). Для определённости рассмотрим систему
кварк-антикварк с противоположно направленными спинами, т. е. состояние
). Для определённости рассмотрим систему
кварк-антикварк с противоположно направленными спинами, т. е. состояние
![]() . Операция зарядового
сопряжения изменяет природу обеих частиц, сохраняя их спиновые состояния:
. Операция зарядового
сопряжения изменяет природу обеих частиц, сохраняя их спиновые состояния:
![]() ,
,
![]() . В результате получается
состояние
. В результате получается
состояние
![]() ,
которое возникло бы при перестановке кварка и антикварка с одновременным обменом
их спинами. Система q
,
которое возникло бы при перестановке кварка и антикварка с одновременным обменом
их спинами. Система q![]() является собственным состоянием оператора
является собственным состоянием оператора ![]() . Поэтому
можно записать
. Поэтому
можно записать
|
|
(17.24) |
Для того чтобы вернуться из состояния
![]() в исходное состояние
в исходное состояние
![]() , нужно осуществить
замену q↔
, нужно осуществить
замену q↔![]() и
вновь поменять спиновые состояния кварков, т. е. одновременно переставить
частицы и их спины. Операция перестановки q и
и
вновь поменять спиновые состояния кварков, т. е. одновременно переставить
частицы и их спины. Операция перестановки q и
![]() в системе их центра масс
эквивалентна операции пространственной инверсии, т.е. приводит к появлению перед
волновой функцией системы множителя полной чётности системы Р. В данном
случае P =Pq
в системе их центра масс
эквивалентна операции пространственной инверсии, т.е. приводит к появлению перед
волновой функцией системы множителя полной чётности системы Р. В данном
случае P =Pq![]() (-1)L
= (+1)(-1)(-1)L = -(-1)L = (-1)L+1, где Pq и
(-1)L
= (+1)(-1)(-1)L = -(-1)L = (-1)L+1, где Pq и
![]() -внутренние
чётности кварка и антикварка (соответственно +1 и -1), а L -их относительный орбитальный момент. Что касается
перестановки спинов кварков, то, если спины кварков параллельны (S
=1), то спиновая функция системы симметрична, т. е. не изменяет знак при
перестановке спинов. Если спины кварков антипараллельны (S = 0), то спиновая функция антисимметрична, т.е. изменяет знак при
перестановке спинов. Обе эти ситуации учитываются введением множителя (-1)S+1 перед волновой функцией
системы при перестановке спинов кварков. Таким образом, зарядовая чётность
системы кварк-антикварк
-внутренние
чётности кварка и антикварка (соответственно +1 и -1), а L -их относительный орбитальный момент. Что касается
перестановки спинов кварков, то, если спины кварков параллельны (S
=1), то спиновая функция системы симметрична, т. е. не изменяет знак при
перестановке спинов. Если спины кварков антипараллельны (S = 0), то спиновая функция антисимметрична, т.е. изменяет знак при
перестановке спинов. Обе эти ситуации учитываются введением множителя (-1)S+1 перед волновой функцией
системы при перестановке спинов кварков. Таким образом, зарядовая чётность
системы кварк-антикварк
![]() (и любой другой системы
фермион-антифермион) является произведением множителя полной чётности системы
(-1)L+1 и множителя (-1)S+1, учитывающего характер
симметрии спиновой волновой функции системы:
(и любой другой системы
фермион-антифермион) является произведением множителя полной чётности системы
(-1)L+1 и множителя (-1)S+1, учитывающего характер
симметрии спиновой волновой функции системы:
|
|
(17.25) |
Из закона сохранения зарядовой четности следует, какое
число фотонов образуется при распаде парапозитрония и ортопозитрония.
Распад позитрония происходит в результате аннигиляции
входящих в его состав e+ и e-, т. е. за счет
сохраняющего зарядовую чётность процесса e+ +
e- → фотоны,
обусловленного электромагнитным взаимодействием. У парапозитрония L
=S =0, а у ортопозитрония L =0, S =1. Поэтому зарядовая чётность парапозитрония
Cпара = (-1)L+S = (-1)0 = +1, а ортопозитрония −
Cорто = (-1)L+S = (-1)1 = -1. Поскольку зарядовая чётность фотона
Cγ = -1, то парапозитроний может распадаться
только на чётное число фотонов, а ортопозитроний − на нечётное
число фотонов. Наиболее вероятен распад с минимально возможным числом фотонов.
Распад с одним фотоном в конечном состоянии запрещён законами сохранения энергии
и импульса. Поэтому парапозитроний преимущественно распадается на 2 фотона, а
ортопозитроний -на 3 фотона.
Кварк-антикварковая (qi![]() j) структура мезонов делает возможным
существование истинно нейтральных мезонов. Все аддитивные квантовые числа
(электрический и барионный заряды, кварковый аромат) в мезоне, состоящем из
кварка и антикварка одного типа, в сумме равны нулю.
j) структура мезонов делает возможным
существование истинно нейтральных мезонов. Все аддитивные квантовые числа
(электрический и барионный заряды, кварковый аромат) в мезоне, состоящем из
кварка и антикварка одного типа, в сумме равны нулю.
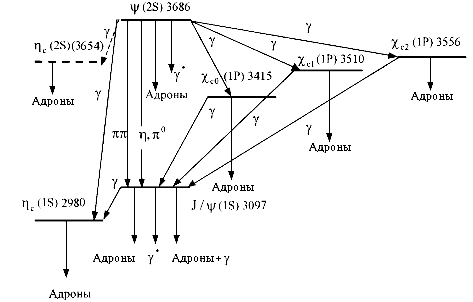
| JPC = | 0-+ | 1-- | 0++ | 1++ | 2++ |
| L = |
0 |
0 |
1 |
1 |
1 |
| S = |
0 |
1 |
1 |
1 |
1 |
Рис. 17.1. Связанные состояния c![]() .
.
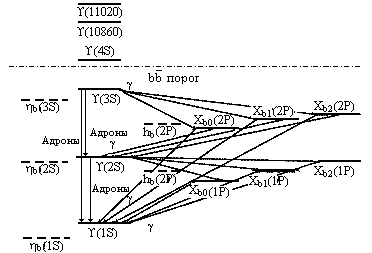
| JPC = | 0-+ | 1-- | 1+- | 0++ | 1++ | 2++ |
| L = | 0 | 0 | 1 | 1 | 1 | 1 |
| S = |
0 |
1 |
0 |
1 |
1 |
1 |
Рис. 17.2. Связанные состояния b![]() .
.
На рис. 17.1 и 17.2 показаны связанные состояния
чармония (c![]() ) и
боттомония (b
) и
боттомония (b![]() ).
Приведены спины
).
Приведены спины
![]() ,
четности P,
зарядовые четности C,
орбитальный L и
спиновый S моменты системы кварк-антикварк.
,
четности P,
зарядовые четности C,
орбитальный L и
спиновый S моменты системы кварк-антикварк.
![]() =
=
![]() +
+
![]() .
.
| Зарядовая чётность С Зарядовая чётность сохраняется в сильных и электромагнитных взаимодействиях и не сохраняется в слабых взаимодействиях. |
Нейтрино. С-, Р-, СР-преобразования
Зарядовая симметрия означает, что если существует
какой-либо процесс с участием частиц, то при замене их на античастицы (зарядовом
сопряжении), процесс также существует и происходит с той же вероятностью.
Зарядовая симметрия отсутствует в процессах с участием нейтрино и антинейтрино.
В природе существуют только левоспиральные нейтрино и правоспиральные
антинейтрино. Если каждую из этих частиц (для определённости будем рассматривать
электронное нейтрино νe и антинейтрино
![]() e) подвергнуть операции зарядового
сопряжения, то они перейдут в несуществующие объекты с лептонными числами и
спиральностями.
e) подвергнуть операции зарядового
сопряжения, то они перейдут в несуществующие объекты с лептонными числами и
спиральностями.
![]() νe =
νe =
![]() |Le
= +1, h = -1> = |Le = -1, h = -1>,
|Le
= +1, h = -1> = |Le = -1, h = -1>,
![]()
![]() e =
e =
![]() |Le
= -1, h = +1> = |Le = +1, h = +1>.
|Le
= -1, h = +1> = |Le = +1, h = +1>.
Таким образом, в слабых взаимодействиях нарушаются
одновременно P- и C-инвариантность. Однако, если над нейтрино
(антинейтрино) совершить две последовательные операции − P- и C‑преобразования (порядок операций не важен), то
вновь получим нейтрино, существующие в природе. Последовательность операций
![]() и
и
![]() (или в обратном порядке) носит
название CP-преобразования. Результат CP‑преобразования (комбинированной
инверсии) νe и
(или в обратном порядке) носит
название CP-преобразования. Результат CP‑преобразования (комбинированной
инверсии) νe и
![]() e следующий:
e следующий:
![]()
![]() νe
= |Le = -1, h = -1> =
νe
= |Le = -1, h = -1> =
![]() e,
e,
![]()
![]()
![]() e = |Le =
+1, h = +1> = νe.
e = |Le =
+1, h = +1> = νe.
Таким образом, для нейтрино и антинейтрино операция,
переводящая частицу в античастицу, это не операция зарядового сопряжения, а
CP-преобразование.
Было высказано предположение, что хотя в слабых
взаимодействиях нет отдельно P- и C-инвариантности, но есть CP‑инвариантность,
т. е. инвариантность к преобразованию комбинированной инверсии
![]()
![]() . Ставилось большое
число экспериментов по проверке CP-инвариантности в слабых процессах.
Так, изучались распады покоящихся π±-мезонов, идущие с нулевым относительным
орбитальным моментом образующихся лептонов
. Ставилось большое
число экспериментов по проверке CP-инвариантности в слабых процессах.
Так, изучались распады покоящихся π±-мезонов, идущие с нулевым относительным
орбитальным моментом образующихся лептонов
π+ → μ+ + νμ, π- → μ-
+
![]() μ.
μ.
Как известно, π± имеет нулевой спин s(π) = 0. В то же время s(μ) = s(ν) = 1/2. Таким образом, если бы P- и C‑инвариантности наблюдались в слабых распадах π±-мезонов, то были бы возможны четыре варианта распада покоящихся π±, удовлетворяющих законам сохранения импульса и углового момента (рис. 17.3).
|
|
a |
|
|
(b) |
|
|
(c) |
|
|
d |
Рис. 17.3. Распады заряженных пионов, разрешённые P- и C‑инвариантностью.Взаимная ориентация векторов импульсов (черные стрелки) и проекций спинов на направление движения (синие стрелки)
Однако в природе реализуются лишь состояния a и
d с «правильной» спиральностью, удовлетворяющие СР‑инвариантности
слабых взаимодействий для
![]() μ и
μ и
![]() μ. Вылетающие в этих случаях
μ. Вылетающие в этих случаях
![]() μ и
μ и
![]() μ в силу законов сохранения
импульса и момента количества движения «навязывают» μ+ и μ- соответственно левую и правую
спиральность. Такие спиральности образующихся в слабых взаимодействиях μ+ и μ- были бы запрещены, если бы мюоны
были ультрарелятивистскими (т. е. имели скорости v ≈ c). Однако распад пиона из состояния покоя идёт с малым
энерговыделением (34 МэВ), мюоны рождаются нерелятивистскими и могут иметь как
правую, так и левую спиральность.
μ в силу законов сохранения
импульса и момента количества движения «навязывают» μ+ и μ- соответственно левую и правую
спиральность. Такие спиральности образующихся в слабых взаимодействиях μ+ и μ- были бы запрещены, если бы мюоны
были ультрарелятивистскими (т. е. имели скорости v ≈ c). Однако распад пиона из состояния покоя идёт с малым
энерговыделением (34 МэВ), мюоны рождаются нерелятивистскими и могут иметь как
правую, так и левую спиральность.
Распады π+ → e+ + νe и π-
→ e-
+
![]() e должны
были бы происходить чаще, чем распады π+ → μ+ + νμ и π-
→ μ-
+
e должны
были бы происходить чаще, чем распады π+ → μ+ + νμ и π-
→ μ-
+
![]() μ,
т.к. в распадах с образованием e+νe и e-
μ,
т.к. в распадах с образованием e+νe и e-![]() e энерговыделение
гораздо больше. Однако большое энерговыделение приводит к подавлению распадов с
образование электронов и позитронов, т.к. в этом случае рождаются релятивистские
частицы.
e энерговыделение
гораздо больше. Однако большое энерговыделение приводит к подавлению распадов с
образование электронов и позитронов, т.к. в этом случае рождаются релятивистские
частицы.
Ультрарелятивистские фермионы, участвующие в
любом слабом процессе, должны иметь значение спиральности h = -1 для
частиц и h = +1 для
античастиц. В указанных распадах нейтрино будут иметь спиральность h = -1.
Поэтому из закона сохранения момента импульса следует, что спин e+ должен
быть направлен против его импульса. позитрон
образовался в результате слабого взаимодействия, и, следовательно, он должен был
бы иметь h(e+) = -1.
Т.к. масса позитрона мала, распад π+ → e+ + νe сильно
подавлен. Но масса μ+ Существенно
больше массы позитрона mμ >> me.
Поэтому он испускается в состоянии, которое является смесью состояний с
«правильной» (h = +1)
и «неправильной» (h = -1)
спиральностями. Распад происходит благодаря примеси «неправильной» компоненты.
Это позволяет объяснить подавление распада π+ → e+ + νe по
сравнению с распадом π+ → μ+ + νμ в
104 раз. В распаде π+ → e+ + νe доля
состояний с «неправильной» спиральностью гораздо меньше, чем в распаде. Величина
подавления распада имеет порядок v/c,
где v −
скорость заряженного лептона, образующегося в распаде π±‑мезона.
Распады нейтральных каонов. Нарушение CP-симметрии
Открытие несохранения комбинированной CP-четности было сделано при изучении свойств K-мезонов. Неожиданности начались с изучения образования и распада Λ-гиперона. В результате реакции π- + p вероятность рождения Λ-частицы оказалась большой по сравнению с её вероятностью распада
Λ → π- + p.
Λ рождались под действием π-мезонов в 1013 раз интенсивнее, чем распадались. Для объяснения этого явления Гелл-Манн, Пайс, Накано, Нишиджима независимо выдвинули гипотезу о том, что в отличие от триплета π-мезонов − π+, π- и π0, существует два дублета K-мезонов (K+, K0) и соответствующие им античастицы (K-, K0), а не казавшийся вполне естественным триплет (K+, K-, K0). Для объяснения поведения Λ-гиперона и дублетов K-мезонов Нишиджима ввел новое квантовое число странность s, которое сохраняется в сильных взаимодействиях и не сохраняется в слабых взаимодействиях. Мезонам K+ и K0 была приписана странность s = +1
s(K+,K0) = 1,
а мезонам K-, K- и Λ-гиперону странность s = -1
s(K-,K0,Λ) = -1.
Объединение K-мезонов в два дублета означало, что
K0 и
K0 являются двумя разными частицами.
Исследования свойств нейтральных K0 и
K0-мезонов представляет особый интерес, т. к.
они позволяют изучить ряд уникальных проявлений принципов квантовой механики.
- Линейные комбинации двух состояний также является состоянием системы. K0 и K0 можно представить как суперпозицию двух других состояний K1 и K2.
- Распады K0 и K0-мезонов показали, что CP-симметрия не является точной симметрией.
Нейтральные мезоны K0 и
K0 являются частицей и античастицей.
Единственное квантовое число, которым различаются K0 и
K0,
− это странность (s(K0) = +1, s(K0) = −1). Поэтому обе частицы
должны иметь одинаковые массы и одинаковые времена жизни. K0 имеет кварковую
структуру d![]() , а
K0 − s
, а
K0 − s![]() . Они по-разному ведут
себя в сильном взаимодействии. Так, согласно закона сохранения странности в
сильных взаимодействиях
K0-мезоны могут образовываться в реакции
. Они по-разному ведут
себя в сильном взаимодействии. Так, согласно закона сохранения странности в
сильных взаимодействиях
K0-мезоны могут образовываться в реакции
| π- + p → Λ + K0, Δs = 0 | (17.26) |
в то время как для K0-мезонов такая реакция запрещена
| π- + p
|
(17.27) |
K0 в сильных взаимодействиях могут образовываться в реакции
| π- + p → n + K0 + K0, | (17.28) |
которая идёт при более
высоких энергиях по сравнению с реакцией (17.26). Распады K0 и
K0-мезонов происходят в результате слабого
взаимодействия. При этом наблюдается ситуация показанная схематически на рис.
17.4.
Если пучком π−-мезонов обстреливать мишень,
то в результате реакции (17.26) из мишени будут вылетать Λ-гипероны и
K0‑мезоны. Так как
время жизни Λ-гиперонов
2.6·10-10 с, они распадаются вблизи мишени на протон и π−-мезон.
Λ → π- + p.
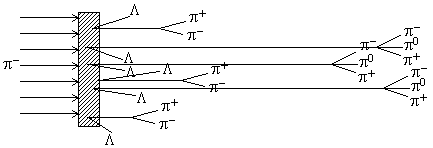
Рис. 17.4. Образование
K0 мезонов в реакции π-
+ p → Λ + K0.
Вблизи мишени наблюдаются также вилки π−π+ от распадов K0‑мезонов
K0 ![]() π−
+ π+.
π−
+ π+.
Однако такие распады наблюдаются лишь для 50% образовавшихся K0-мезонов.
В оставшихся 50% случаев K0 распадается гораздо дальше от мишени на 3 π-мезона.
Операция зарядового сопряжения
![]() превращает
K0 в
K0, а
K0 − в
K0.
превращает
K0 в
K0, а
K0 − в
K0.
![]() |К0>
= -|K0>,
|К0>
= -|K0>, ![]() |K0>
= -|К0>.
|K0>
= -|К0>.
Нейтральные каоны рождаются в сохраняющем изоспин и
странность сильном взаимодействии, а распадаются в результате слабого
взаимодействия на два или три пионы. В слабом взаимодействии странность может не
сохраняться. Поэтому, находясь в свободном состоянии, K0- и
K0-мезоны могут переходить друг в друга в
результате двух последовательных виртуальных процессов с изменением странности в
каждом из них на единицу Δs = 1.
В результате возникает смешивание состояний
K0 и
K0. Механизм этого смешивания можно
описать с помощью кварковой диаграммы (рис. 17.5).
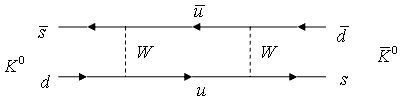
Рис. 17.5. Кварковая диаграмма, поясняющая механизм смешивания K0 и K0.
Действие операторов ![]() ,
, ![]() и
и
![]()
![]() на волновые функции K0 и
K0 можно записать в виде:
на волновые функции K0 и
K0 можно записать в виде:
![]() |К0> = -|K0>,
|К0> = -|K0>, ![]() |K0>
= -|К0>,
|K0>
= -|К0>,
![]() |К0>
= -|К0>,
|К0>
= -|К0>, ![]() |K0> =
-|K0>,
|K0> =
-|K0>,
![]()
![]() |К0> = |K0>,
|К0> = |K0>, ![]()
![]() |K0> = |К0>,
|K0> = |К0>,
т. е. состояния K0 и
K0 не имеют определенного значения
СР‑четности. Однако из состояний K0 и
K0 можно построить линейную комбинацию
состояний
![]() и
и
![]() , имеющую определенные
значения СР-четности:
, имеющую определенные
значения СР-четности:
![]() ,
,
![]() .
.
СР-четности состояний
![]() и
и
![]()
![]()
![]() |
|![]() >
= +1|
>
= +1|![]() >,
>,
![]()
![]() |
|![]() > =
-1|
> =
-1|![]() >.
>.
K1 и K2 не являются частицей и
античастицей и поэтому могут иметь разные характеристики распада.
Проанализируем выполнение закона сохранения
комбинированной СР-четности в распадах
K0-мезонов на 2 и 3 π‑мезона.
Двухпионные π+π− и трехпионные π+π−π0
системы при нулевом орбитальном моменте L являются собственными состояниями ![]()
![]() -оператора. Для двухпионной системы
-оператора. Для двухпионной системы
π+π−-система, L = 0.
Операция ![]() эквивалентна обмену π+ π−-мезонов местами. При таком обмене волновая функция приобретает множитель
(-1)L.
эквивалентна обмену π+ π−-мезонов местами. При таком обмене волновая функция приобретает множитель
(-1)L.
![]() |π+π->
=
|π+π->
= ![]() |π+>
|π+>
![]() |π->
(-1)L = +1 |π+π->.
|π->
(-1)L = +1 |π+π->.
Операция ![]() превращает π+
в π−и π−в π+, т. е. она тоже
эквивалентна обмену местами π+π−-мезонов.
превращает π+
в π−и π−в π+, т. е. она тоже
эквивалентна обмену местами π+π−-мезонов.
![]() |π+π->
= (-1)L |π+π->
= +1|π+π->,
|π+π->
= (-1)L |π+π->
= +1|π+π->,
![]()
![]() |π+π->
= (-1)2L |π+π->
= |π+π->.
|π+π->
= (-1)2L |π+π->
= |π+π->.
Собственное значение ![]()
![]() -оператора
двухпионной системы в состоянии L = 0 равно +1.
-оператора
двухпионной системы в состоянии L = 0 равно +1.
Для трехпионной системы
π+π-π0
система, L = 0.
![]() |π+π-π0>
=
|π+π-π0>
= ![]() |π+>
|π+>
![]() |π->
|π->
![]() |π0>
(-1)L = -1 |π+π-π0>,
|π0>
(-1)L = -1 |π+π-π0>,
![]() |π+π-π0>
= |π+π-π0> (-1)L = +1|π+π-π0>,
|π+π-π0>
= |π+π-π0> (-1)L = +1|π+π-π0>,
![]()
![]() |π+π-π0> = -1|π+π-π0>.
|π+π-π0> = -1|π+π-π0>.
Собственное значение ![]()
![]() -оператора
трехпионной системы (L = 0) равно −1 .
-оператора
трехпионной системы (L = 0) равно −1 .
Таким образом, состояния |![]() > и |
> и |![]() >
имеют определенные значения CP-четности, но не имеют определенного значения
странности s. Можно записать
>
имеют определенные значения CP-четности, но не имеют определенного значения
странности s. Можно записать
|К0> = (|![]() >
+ |
>
+ |![]() >)/
>)/![]() ,
,
|K0>
= (|![]() > −
|
> −
|![]() >)/
>)/![]() .
.
Т.е. каждая из частиц K0 и
K0 является суперпозицией
состояний
![]() и
и
![]() .
Т.к.
.
Т.к. ![]() ) = +1,
) = +1,![]() распадается на 2 π-мезона. Среднее время жизни состояния τ(
распадается на 2 π-мезона. Среднее время жизни состояния τ(![]() ) ~ 0.9·10-19 с. В свою
очередь CP(
) ~ 0.9·10-19 с. В свою
очередь CP(![]() ) = -1,
поэтому
) = -1,
поэтому
![]() распадается на 3 π-мезона, также без нарушения комбинированной четности. Время
жизни
распадается на 3 π-мезона, также без нарушения комбинированной четности. Время
жизни
![]() должно быть больше времени жизни
должно быть больше времени жизни
![]() из-за меньшего фазового объема для продуктов распада
из-за меньшего фазового объема для продуктов распада ![]() ) ~
5·10-8 с).
) ~
5·10-8 с).![]() ,
то вблизи мишени наблюдаются распады этой компоненты на 2
,
то вблизи мишени наблюдаются распады этой компоненты на 2 ![]() -мезона.
На большем расстоянии от мишени наблюдается распад компоненты
-мезона.
На большем расстоянии от мишени наблюдается распад компоненты
![]() на 3 π-мезона.
на 3 π-мезона.
В природе существует две линейно независимые комбинации
состояний
![]() и
и
![]() ,
которые отвечают частицам с различными массами и средним временем жизни:
,
которые отвечают частицам с различными массами и средним временем жизни:
m(К0) = 497.67 МэВ
τ(![]() )
= 5.2·10-8 c,
)
= 5.2·10-8 c,
τ(![]() )
= 0.9·10-10 c.
)
= 0.9·10-10 c.
Основные каналы распада
![]()
|
π+π- | 68.6%, |
| π0π0 | 31.4% |
Основные каналы распада
![]()
|
π0π0π0 | 21.1%, |
| π+π-π0 | 12.6% | |
| π+μ- |
27.1% | |
| π+е- |
38.8% |
Рассчитанная в предположении
сохранения СР‑инвариантности разность масс
![]() и
и
![]()
m(![]() )
- m(
)
- m(![]() )
=(3.491 + 0.009)·10-12 МэВ.
)
=(3.491 + 0.009)·10-12 МэВ.
Если СР-инвариантность имеет место, можно считать:
|![]() >|
>|![]() |
|![]() >,
|
>,
|![]() >
> ![]() |
|![]() >.
>.
Однако, в 1964 г. Дж. Кронин и В.Фитч обнаружили, что в
распадах нейтральных каонов происходит нарушение СР‑инвариантности. Оказалось,
что существует малая, но конечная вероятность распада
![]() -мезона на два π-мезона
-мезона на два π-мезона
![]() → π++ π−,
→ π++ π−,
в котором собственное
значение
![]()
![]() -оператора
в конечном состоянии имеет СР = +1:
-оператора
в конечном состоянии имеет СР = +1:
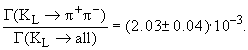
Этот результат означает, что нельзя отождествлять состояние
![]() с
с
![]() и
и
![]() с
с
![]()
Вместо этого можно следующим образом определить состояния
![]() и
и
![]()
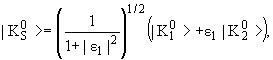
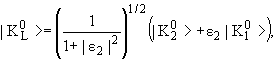
где ε1 и ε2 - малые комплексные числа.
1964 г. В. Фитч, Дж. Кронин обнаружили нарушение CP‑четности в распадах K0-мезонов.
В. Л. Фитч:«Общий вид использованной нами в этих экспериментах
аппаратуры показан на рис. 1. Она представляла собой двухплечовой спектрометр, в
каждом плече которого до и после отклоняющего магнита расположены искровые
камеры, фиксирующие траектории частиц. Черенковские сцинтилляционные счетчики в
обоих плечах были включены на совпадения и вырабатывали сигналы, запускающие
искровые камеры, и треки частиц фотографировались на пленку. Аппаратура была
расположена в пучке нейтральных частиц брукхейвенского протонного синхротрона на
таком расстоянии, что
![]() -мезоны должны были уже
распасться и в пучке оставались только
-мезоны должны были уже
распасться и в пучке оставались только ![]()
![]()
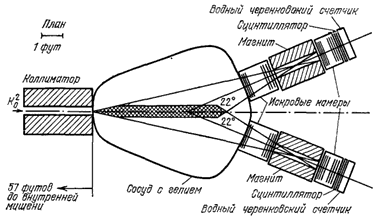
Рис.1. Общий вид установки.
Распад на два пиона выделялся среди огромного
количества обычных трехчастичных распадов ![]()
![]()
![]()
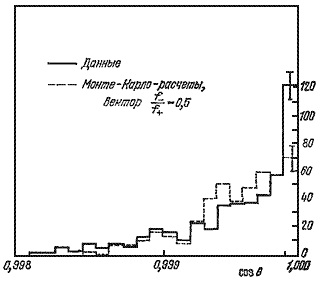
Рис. 2. Угловое распределение событий в
соответствующем интервале масс.
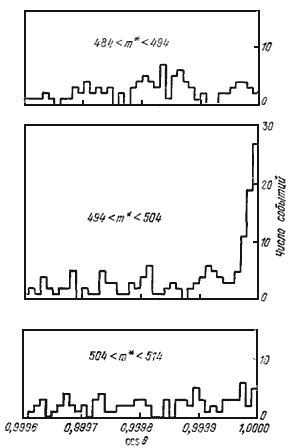
Рис.3. Угловое
распределение событий, полученное после точной обработки, в трех интервалах
масс.
Нарушение СР-четности невелико (доля распадов нейтральных каонов с нарушением СР-инвариантности ≈10-3), однако само его существование важно для фундаментальной физики.
Нобелевская премия по физике
1980 г. − В. Фитч, Дж. Кронин.
За открытие
нарушения фундаментальных принципов симметрии в распаде нейтральных K-мезонов.
 Вал Фитч (р. 1923) |
 Джеймс Кронин (р. 1931) |
Операция обращения времени
Операция обращения времени Т сводится к замене
t → −t. Преобразование
пространственных координат
![]() , импульса
, импульса
![]() и момента импульса
и момента импульса
![]() при операции обращения времени:
при операции обращения времени:
![]()
В результате Т-преобразования происходит
изменение знаков импульса, момента импульса и меняются местами начальное и
конечное состояния. Операция обращения времени превращает исходное движение
в обратное.
Импульс и момент количества движения при обращении
времени изменяют свои направления на противоположные, так как эти величины по
определению содержат производные по времени d![]() /dt (импульс
/dt (импульс
![]() = m(d
= m(d![]() /dt), момент количества движения
/dt), момент количества движения
![]() = [
= [![]()
![]() ]). При обращении времени
энергия не изменяется.
]). При обращении времени
энергия не изменяется.
На рис. 17.6 показано Т-преобразование процесса
распада π-‑мезона:
|
|
||
|
|
||
| Т: |
|
|
|
|
Рис. 17.6. Т-преобразование процесса распада π-‑мезона.
Из требования Т-инвариантности следует равенство сечений прямого и обратного процессов, что позволяет проверить выполнение Т‑инвариантности в различных процессах.
Спиральность частицы
![]() инвариантна по
отношению к обращению времени,
инвариантна по
отношению к обращению времени,
![]() − спин частицы,
− спин частицы,
![]() − ее импульс.
− ее импульс.
При обращении времени как импульс, так и спин (момент
количества движения) изменяют знаки. Следовательно, спиральность, являющаяся
произведением этих величин, должна сохраняться.
Рассмотрим, как изменяются при операции обращения
времени векторный и скалярный потенциалы, напряженность электрического и
магнитного поля. По определению
![]()
и
![]() = rot
= rot![]() ,
,
где
φ и ![]() − скалярный и векторный
потенциалы электромагнитного поля,
− скалярный и векторный
потенциалы электромагнитного поля,
![]() − напряженность электрического поля и
− напряженность электрического поля и
![]() − напряженность
магнитного поля. Уравнение движения заряда в электромагнитном поле будет
− напряженность
магнитного поля. Уравнение движения заряда в электромагнитном поле будет
![]()
Уравнения движения инвариантны по отношению к обращению времени, поэтому вместе с заменой t на -t надо изменить знак магнитного поля, то есть уравнение движения не изменяется, если провести замену
t → -t,
![]() →
→
![]() ,
,
![]() → -
→ -![]() .
.
При этом скалярный потенциал не изменяется, а векторный потенциал изменяет знак:
φ → φ,
![]() → -
→ -![]() .
.
Таким образом, обращение времени оставляет скалярный
потенциал и напряженность электрического поля неизменными, а векторный потенциал
и напряженность магнитного поля при этом изменяют направление на
противоположное.
Уравнения Максвелла Т-инвариантны. Сильное
взаимодействие тоже Т-инвариантно. Одно из следствий Т‑инвариантности
– равные вероятности прямых и обратных реакций a + b ↔ c
+ d. Многочисленные проверки не обнаружили
нарушения этого равенства. Однако точность таких проверок не слишком высока –
обычно на уровне 10-2 – 10-3.
Обнаружение нарушения CP-инвариантности
позволяет сделать очень важный для физики вывод о Т-инвариантности нашего
мира. Дело в том, что существует CPT-теорема. Смысл CPT‑теоремы
можно свести к следующему утверждению: наш мир и мир, полученный из нашего путём
зарядового сопряжения, пространственной инверсии и обращения времени, идентичны.
То есть наш мир и мир, являющийся его зеркальным отражением с заменой всех
частиц на античастицы и движением всех объектов в обратном направлении,
идентичны. Любой мыслимый гамильтониан инвариантен относительно CPT преобразования.
CPT-инвариантность является фундаментальным физическим принципом, который
следует из требований специальной теории относительности и соблюдения принципа
причинности.
СРТ-теорема и
нарушение CP-инвариантности приводят к дилемме. Либо нет T-инвариантности
(она должна нарушаться, если справедлива CPT-теорема), либо CPT-теорема
не верна. Все известные факты свидетельствуют в пользу справедливости СРТ‑теоремы.
СРТ-инвариантность следует из общих принципов квантовой теории поля. Её
нарушение потребовало бы радикально изменить такие основы этой теории, как
принцип причинности и связь спина с квантовой статистикой. Простейшие тесты
СРТ‑инвариантности – равенство масс и времён жизни частиц и античастиц.
Лучший известный тест – ограничение на разность масс K0 и её античастицы
K0
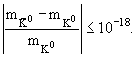
Нарушение CP-инвариантности убедительно, хотя и
косвенно, доказывает нарушение T-инвариантности в распадах нейтральных
каонов. Распад нейтральных каонов – не единственный известный процесс, в котором
обнаружено нарушение CP-, а значит и T‑инвариантности.
Исследования распадов B0-мезонов показали, что и в этом случае
также нарушается СР-четность.
Нарушение СР-симметрии в распадах В-мезонов наблюдалось
в 2001 г. в эксперименте BaBar на ускорителе
Стэндфордского центра линейных ускорителей SLAC (США) и в экспериментах на
ускорителе KEK (Япония).
Объяснение причин нарушения СР-инвариантности в системе
B-мезонов
является одной из фундаментальных проблем физики. В частности на
B-фабриках планируется
исследование распадов в области энергии ![]() (4s) резонанса, который распадается на
B+B- и B0В-мезоны. Преимущество рождения
B-мезонов на B‑фабриках состоит в
большом отношении числа нужных событий к фону. В частности на ускорителе LHC
создан специальный детектор LHCb, предназначенный для изучения образования и распада
прелестных частиц, содержащих b-кварк. Выяснение причин нарушения СР‑четности
является одной из фундаментальных проблем современной физики.
(4s) резонанса, который распадается на
B+B- и B0В-мезоны. Преимущество рождения
B-мезонов на B‑фабриках состоит в
большом отношении числа нужных событий к фону. В частности на ускорителе LHC
создан специальный детектор LHCb, предназначенный для изучения образования и распада
прелестных частиц, содержащих b-кварк. Выяснение причин нарушения СР‑четности
является одной из фундаментальных проблем современной физики.
| СP- и T-инвариантность СP- и T-инвариантность сохраняется в сильных и электромагнитных взаимодействиях и не сохраняется в слабых взаимодействиях. |