11. Адроны - системы связанных цветных кварков
К середине шестидесятых годов XX столетия, когда наряду
с протоном и нейтроном было открыто несколько десятков «элементарных» частиц,
стало ясно, что эти «элементарные» частицы состоят из более фундаментальных
частиц. В 1964 г. Независимо друг от друга
М. Гелл-Манн и
Д. Цвейг предложили
составную кварковую модель адронов.
Кварки объединяются в частицы, называемые адронами.
Термин «адрон» происходит от греческого «хадрос» – сильный и отражает свойство
адронов участвовать в сильных взаимодействиях. Адроны
– связанные системы кварков и антикварков. Адроны существуют двух типов –
барионы и мезоны.
- Барионы (барионный заряд В
=
+1) - частицы, состоящие из
трёх кварков (qqq), и являющиеся фермионами (J
= 1/2, 3/2, …). К числу
барионов относятся, например, протон и нейтрон.
- Антибарионы (В
=
-1) состоят из трех
антикварков (
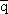 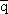 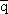 ). Антипротон и антинейтрон входят с группу антибарионов. ). Антипротон и антинейтрон входят с группу антибарионов.
- Мезоны (В
= 0), состоящие
из кварка и антикварка (q
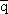 ), занимают промежуточное положение.
Мезоны имеют целочисленное значение спина и являются бозонами (J
= 0, 1, 2, …). ), занимают промежуточное положение.
Мезоны имеют целочисленное значение спина и являются бозонами (J
= 0, 1, 2, …).
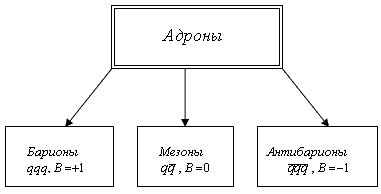
Рис. 11.1. Типы адронов и их кварковый состав.
Квантовые числа кварков, образующих адрон, определяют
квантовые числа адронов. Адроны имеют определенные значения электрического
заряда Q, спина J, чётности P, изоспина I. Квантовые
числа s (странность), c (очарование или шарм),
b (bottom) и
t
(top) разделяют адроны на обычные нестранные частицы
(р,
n, π, …), странные частицы (K,
Λ, Σ, …), очарованные (D, Λc, Σc, …) и боттом-частицы (B, Λb, Ξb ). t‑кварк имеет время
жизни ≈ 10-25
с, поэтому за такое короткое время он не успевает
образовать адрон.
Всё многообразие адронов возникает в результате
различных сочетаний u-, d-, s-, c-, b-кварков,
образующих связанные состояния.
Квантовые характеристики кварков приведены в табл.
11.1. Каждый кварк имеет еще три цветные степени свободы (красный, синий,
зеленый). Цветные степени свободы в таблице не указаны. Античастицы кварков – антикварки.
Таблица
11.1
Характеристики
кварков
| Характеристика |
Тип
кварка (аромат) |
| d |
u |
s |
c |
b |
t |
Электрический заряд Q,
в единицах е |
-1/3 |
+2/3 |
-1/3 |
+2/3 |
-1/3 |
+2/3 |
| Барионное число B |
+1/3 |
| Спин J |
1/2 |
| Четность P |
+1 |
| Изоспин I |
1/2 |
0 |
| Проекция изоспина I3 |
-1/2 |
+1/2 |
0 |
| Странность s |
0 |
0 |
-1 |
0 |
0 |
0 |
| Очарование (charm) c |
0 |
0 |
0 |
+1 |
0 |
0 |
| Bottom b |
0 |
0 |
0 |
0 |
-1 |
0 |
| Top t |
0 |
0 |
0 |
0 |
0 |
+1 |
| Масса конституэнтного кварка mс2,
ГэВ |
0.33 |
0.33 |
0.51 |
1.8 |
5 |
180 |
| Масса токового кварка |
4-8 МэВ |
1.5-4 МэВ |
80-130 МэВ |
1.1-1.4 ГэВ |
4.1-4.9 ГэВ |
174±5 ГэВ |
Квантовые характеристики
антикварков приведены в табл. 11.2.
Таблица
11.2
Характеристики
антикварков
| Характеристика |
Тип
кварка (аромат) |
| d |
u |
s |
c |
b |
t |
Электрический заряд Q,
в единицах е |
+1/3 |
-2/3 |
+1/3 |
-2/3 |
+1/3 |
-2/3 |
| Барионное число B |
-1/3 |
| Спин J |
1/2 |
| Четность P |
-1 |
| Изоспин I |
1/2 |
0 |
| Проекция изоспина I3 |
+1/2 |
-1/2 |
0 |
| Странность s |
0 |
0 |
+1 |
0 |
0 |
0 |
| Очарование (charm) c |
0 |
0 |
0 |
-1 |
0 |
0 |
| Bottom b |
0 |
0 |
0 |
0 |
+1 |
0 |
| Top t |
0 |
0 |
0 |
0 |
0 |
-1 |
| Масса конституэнтного кварка mс2,
ГэВ |
0.33 |
0.33 |
0.51 |
1.8 |
5 |
180 |
| Масса токового кварка |
4-8 МэВ |
1.5-4 МэВ |
80-130 МэВ |
1.1-1.4 ГэВ |
4.1-4.9 ГэВ |
174±5 ГэВ |
Кварки не существуют в свободном состоянии, а заключены
в кварковых системах – адронах. Поэтому им нельзя освободиться от взаимодействия
с другими кварками, находящимися в том же объеме и связывающими их в адрон
глюонами.
Барионное число B − квантовая характеристика частиц, отражающая установленный на опыте ещё
до открытия кварков закон сохранения числа барионов. Так например, протон без
нарушения законов сохранения энергии, импульса, момента количества движения,
электрического заряда мог бы распасться на позитрон e+ и γ-квант
p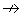 e+
+ γ e+
+ γ
или
на положительно заряженный пион π+ и γ-квант
p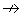 π+
+ γ. π+
+ γ.
Однако такие распады не наблюдаются. Это можно понять, приписав протону
барионное число В = +1 и считать, что все частицы, состоящие из трёх
кварков, имеют барионное число, равное плюс единице. Мезоны имеют барионное
число В = 0. Антибарионы имеют
барионное число В = -1.
Лептоны имеют барионное число В = 0.
Все имеющиеся опытные данные свидетельствуют о
существовании закона сохранения барионного числа (заряда) или закона сохранения
числа барионов:
|
Закон сохранения числа
барионов
Во всех процессах,
происходящих в природе, разность числа
барионов и антибарионов
сохраняется |
Барионное число является аддитивным квантовым числом.
Барионные числа адронов – следствие их кварковой структуры. Кваркам приписывают
барионное число В = +1/3, а антикваркам В = -1/3. Тогда все частицы, состоящие из трех кварков (барионы), будут иметь
барионное число В = +1, частицы из трех
антикварков (антибарионы) − B
= -1, а частицы
из кварка и антикварка (мезоны) − B = 0.
В отличие от точечных кварков, адроны протяжённые
объекты, т. е. имеют размер (≈ 1 Фм).
Среднеквадратичные зарядовые радиусы протона p, пиона π и каона K

дают представление о размерах этих адронов.
Ф. Вилчек:
«Кварки рождаются свободными, но встречаются только связанными… В начале
двадцатого века, после пионерских экспериментов Резерфорда, Гейгера и Марсдена,
физики открыли, что большая часть массы и весь положительный заряд внутри атома
сконцентрированы в крошечных ядрах. В 1932 г. Чедвик открыл нейтроны, которые
вместе с протонами могли бы рассматриваться как составляющие атомного ядра.
Однако известных тогда сил гравитации и электромагнетизма было недостаточно, для
того чтобы связать протоны и нейтроны в такие малые объекты, как наблюдаемые
ядра. Физики столкнулись с новым видом взаимодействия, самым сильным в природе.
Объяснение этой новой силы стало основной задачей теоретической физики.
Для решения указанной проблемы физики в течение многих
лет собирали данные, полученные, в основном, из изучения результатов
столкновений протонов и нейтронов. Однако результаты этих исследований
оказывались громоздкими и сложными.
Если бы частицы в указанных экспериментах были
фундаментальными (неделимыми), то после их столкновения следовало бы ожидать те
же частицы, только выходящие по измененным траекториям. Вместо этого на выходе,
после столкновения, часто оказывалось множество частиц. Конечное состояние могло
содержать как несколько копий исходных частиц, так и другие частицы. Многие
новые частицы были открыты именно таким образом. Несмотря на то, что эти
частицы, называемые адронами, были нестабильны, их свойства были очень схожи со
свойствами нейтронов и протонов. Тогда характер исследования изменился. Уже не
казалось естественным полагать, что речь идет просто об изучении новой силы,
связывающей протоны и нейтроны в атомные ядра. Скорее, открылся новый мир
явлений. Этот мир состоял из множества новых неожиданных частиц, преобразующихся
друг в друга удивительно большим количеством способов. Отражением изменения во
взглядах стало и изменение в терминологии.
Вместо ядерных сил физики стали говорить о сильном
взаимодействии.
В начале 1960-х годов Мюррей Гелл-Ман и Джордж Цвейг
совершили огромный прорыв в теории сильного взаимодействия, предложив концепцию
кварков. Если вы представите, что адроны не являются фундаментальными частицами,
а состоят из некоторого числа неделимых кварков, то все становится на свои
места. Десятки наблюдаемых адронов, по крайней мере в грубом приближении, можно
объяснить различными возможными способами соединений всего трех типов
(«ароматов») кварков. Один и тот же набор кварков может иметь различные
пространственные орбиты и разнообразные спиновые конфигурации. Энергия такой
системы будет зависеть от всех этих факторов, и таким образом получатся
состояния с разными энергиями, соответствующие частицам с разными массами,
согласно формуле m = E/c2. Это аналогично тому, как спектр
возбужденных состояний в атоме мы понимаем как проявление различных орбит и
спиновых конфигураций электронов. (Правда, энергии взаимодействия электронов в
атомах относительно малы, и влияние этих энергий на полную массу атома
незначительно.)
Тем не менее, правила использования кварков для
описания реалистических моделей казались довольно странными и непонятными.
Предполагалось, что кварки едва ли чувствуют
присутствие друг друга, когда находятся рядом, но если вы попытаетесь их
изолировать друг от друга, то обнаружите, что это невозможно. Усиленные попытки
найти изолированный кварк успехом так и не увенчались. Наблюдаемыми оказались
только связанные состояния кварка с антикварком (мезоны) и трех кварков
(барионы). Этот принцип, выведенный из экспериментальных наблюдений, назвали
конфайнментом. Однако возвышенное название не сделало само явление менее
таинственным.
Была у кварков и еще одна примечательная особенность.
Предполагалось, что их электрические заряды являются дробными (1/3 или 2/3) по
отношению к основному единичному заряду, например, электрона или протона. Все
остальные наблюдаемые заряды известны с большой точностью и кратны основному.
Кроме того, тождественные кварки не подчиняются обычным правилам квантовой
статистики. Эти правила требуют, чтобы кварки, как частицы со спином 1/2, были
фермионами с антисимметричными волновыми функциями (если не учитывать цветовую
симметрию). Однако наблюдаемые данные о барионах не могут быть объяснены с
помощью антисимметричных волновых функций они должны быть симметричными.
Атмосфера таинственности вокруг свойств кварков еще
более сгущалась, когда Дж. Фридман. Г. Кендалл, Р. Тейлор и их коллеги на
линейном ускорителе в Стэнфорде (SLAC) направили фотоны с
высокой энергией на прогоны и обнаружили внутри нечто вроде кварков. Неожиданным
было то. что при сильных столкновениях кварки двигаются (точнее, переносят
энергию и импульс) так, как если бы они были свободными частицами. До этого
эксперимента большинство физиков предполагало, что каким бы ни было сильное
взаимодействие кварков, оно должно заставить кварки обильно излучать энергию, и,
следовательно, после резкого ускорения энергия движения должна быстро
рассеиваться»[*].
Таблица
Некоторые барионы
| Частица |
Кварковая
структура |
Масса
mc2, МэВ |
Время жизни
t (сек) или
ширина Г |
Спин-четность,
изоспин JP(I) |
Основные
моды распада |
| p |
uud |
938.27 |
>1032 лет |
1/2+(1/2) |
|
| n |
udd |
939.57 |
885.7±0.8 |
1/2+(1/2) |
pe-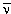 e e |
| Λ |
uds |
1116 |
2.6×10-10 |
1/2+(0) |
pπ-, nπ0 |
| Σ+ |
uus |
1189 |
0.80×10-10 |
1/2+(1) |
pπ0, nπ+ |
| Σ0 |
uds |
1193 |
7.4×10-20 |
1/2+(1) |
Λγ |
| Σ- |
dds |
1197 |
1.5×10-10 |
1/2+(1) |
nπ- |
| Ξ0 |
uss |
1315 |
2.9×10-10 |
1/2+(1/2) |
Λπ0 |
| Ξ- |
dss |
1321 |
1.6×10-10 |
1/2+(1/2) |
Λπ- |
|
| Δ++ |
uuu |
1230-1234 |
115-125 МэВ |
3/2+(3/2) |
(n или p) + p |
| Δ+ |
uud |
| Δ0 |
udd |
| Δ+ |
ddd |
| Σ(1385)+ |
uus |
1383 |
36 МэВ |
3/2+(1) |
Λπ, Σπ |
| Σ(1385)0 |
uds |
1384 |
36 МэВ |
| Σ(1385)- |
dds |
1387 |
39 МэВ |
| Ξ(1530)0 |
uss |
1532 |
9.1 МэВ |
3/2+(1/2) |
Ξπ |
| Ξ(1530)- |
dss |
1535 |
9.9 МэВ |
| Ω- |
sss |
1672 |
0.82×10-10 |
3/2+(0) |
ΛK-, Ξ0π- |
|
| N(1440)+ |
uud |
1430-1470 |
250-450 МэВ |
1/2+(1/2) |
n(π)+p(2π), Δπ |
| N(1440)0 |
udd |
| N(1520)+ |
uud |
1515-1530 |
110-135 МэВ |
3/2-(1/2) |
n(π)+p(2π), Δπ |
| N(1520)0 |
udd |
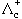 |
udc |
2285 |
2.0×10-13 |
1/2+(0) |
(n или p)+др. |
| Σc(2455)++ |
uuc |
2453 |
2.2 МэВ |
1/2+(1) |
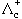 π π |
| Σc(2455)+ |
udc |
2451 |
< 4.6 МэВ |
| Σc(2455)0 |
ddc |
2452 |
2.2 МэВ |
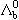 |
udb |
5620 |
1.4×10-13 |
1/2+(0) |
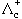 e- e- |
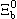 |
usb |
5792 |
1.4×10-12 |
1/2+ (1/2) |
Ξ-e- X X |
Таблица
Некоторые мезоны
| Частица |
Кварковая
структура |
Масса
mc2, МэВ |
Время жизни
t (сек) или
ширина Г |
Спин-четность,
изоспин JP(I) |
Основные
моды распада |
| π+ |
u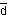 |
139.57 |
2.6×10-8 |
0-(1) |
νμμ+ |
| π- |
d |
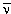 μμ- μμ- |
| π0 |
u - d
- d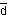 |
134.98 |
8.4×10-17 |
2γ |
| K+ |
u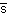 |
494 |
1.2×10-8 |
0-(1/2) |
νμμ+, π0π+ |
| K- |
s |
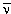 μμ-, π0π- μμ-, π0π- |
| K0 |
d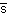 |
498 |
8.9×10-11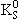 |
0-(1/2) |
π+π-, π0π0 |
|
K0 |
s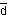 |
5.2×10-8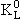 |
πeν, πμν, 3π |
|
| η |
u + d
+ d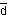 - 2s
- 2s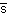 |
548 |
1.29 кэВ |
0-(0) |
2γ, 3π |
| η' |
u + d
+ d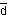 + s
+ s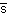 |
958 |
0.20 МэВ |
0-(0) |
η2π, ρ0γ |
| ρ+ |
u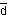 |
776 |
150 МэВ |
1-(1) |
ππ |
| ρ- |
d |
ππ |
| ρ0 |
u - d
- d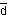 |
776 |
150 МэВ |
ππ |
| ω |
u + d
+ d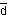 |
783 |
8.5 МэВ |
1-(0) |
3π |
| ¢ |
s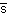 |
1019 |
4.3 МэВ |
1-(0) |
K+K-,
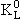 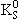 |
|
| D+ |
c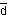 |
1869 |
1.0×10-12 |
0-(1/2) |
K+др., e+др., μ+др. |
| D- |
d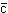 |
K+др., e+др., μ+др. |
| D0 |
c |
1865 |
4.1×10-13 |
0-(1/2) |
K+др., e+др., μ+др. |
|
D0 |
u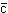 |
K+др., e+др., μ+др. |
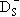 |
c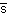 |
1968 |
4.9×10-13 |
0-(0) |
K+др. |
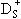 |
s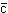 |
K+др. |
| B+ |
u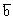 |
5279 |
1.7×10-12 |
0-(1/2) |
D+др.,
D*+др., ν+др. |
| B- |
b |
D+др.,
D*+др., ν+др. |
| B0 |
d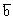 |
5279 |
1.5×10-12 |
0-(1/2) |
D+др.,
D*+др., ν+др. |
|
B0 |
b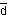 |
D+др.,
D*+др., ν+др. |
| J/ψ |
c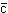 |
3097 |
91 кэВ |
1-(0) |
адроны, 2e,
2μ |
| Y |
b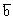 |
9460 |
53 кэВ |
1-(0) |
τ+τ-, μ+μ-, e+e- |
Кварки, образующие адроны, могут находиться в
состояниях с различными орбитальными моментами lq и в состояниях с различными
значениями радиального квантового числа n. Так как кварк имеет
положительную чётность, а антикварк
-
отрицательную, чётности барионов, антибарионов и мезонов определяются
соотношениями


где
L - результирующий орбитальный момент кварков в адроне.
Аналогичным образом можно получить формулу для чётности
мезона/антимезона:

Спины кварков могут быть ориентированы различным
образом. Поэтому для одной и той же кварковой комбинации допустимы различные
значения полного момента и чётности JP. Энергия (масса)
фиксированной кварковой комбинации зависит от JP и других квантовых чисел, таких как
изоспин, т. е. для каждой кварковой комбинации получается набор энергий (масс).
Такова суть спектроскопии адронов, которая по существу не отличается от атомной
или ядерной спектроскопии. Отличие в атоме состоит в том, что если в атоме (или
в ядре) с определённым внутренним составом частиц изменяется энергия и квантовые
числа, то это означает переход в другое состояние этого же
атома (ядра). В физике адронов изменение энергии (массы) и квантовых чисел
фиксированной кварковой комбинации означает переход к другой частице.
Адроны - бесцветные образования цветных кварков
Почему существует столь
ограниченный набор связанных кварковых структур - трёхкварковые и кварк-антикварковые состояния? Для
ответа на этот вопрос нужно пояснить понятие бесцветного состояния.
Кварковая модель в своем первоначальном варианте не содержала понятия «цвет».
Исходная модель смогла представить все многочисленное семейство адронов всего
лишь в виде трех кварковых комбинаций −
qqq (барионы),
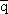 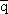 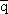 (антибарионы) и q (антибарионы) и q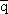 (мезоны). Однако
оставалось неясным, почему других комбинаций кварков, например, qq, (мезоны). Однако
оставалось неясным, почему других комбинаций кварков, например, qq,
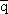 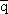 , qq , qq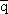 , q , q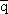 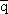 ,
qqqq, qq ,
qqqq, qq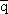 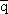 , q , q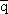 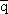 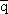 и т.д. в природе нет, да и сами
отдельные кварки не наблюдаются. Кроме того, были известны барионы из трех
тождественных кварков – uuu (Δ++-резонанс),
ddd (Δ-‑резонанс),
sss (Ω--гиперон), в которых
кварки находились в одинаковых квантовых состояниях, что противоречило принципу
Паули. Все эти трудности начального варианта кварковой модели снимались
введением для кварков еще одного квантового числа, названного цветом. Это
квантовое число должно было иметь три возможных значения с тем, чтобы можно было
восстановить принцип Паули для барионов, построенных из трех кварков одинакового
аромата. Эти три возможных значения цвета – красный (к), зеленый (з)
и синий (с) – можно рассматривать как три проекции своеобразного
цветового спина в трехмерном цветовом пространстве (с осями К,
З. С). и т.д. в природе нет, да и сами
отдельные кварки не наблюдаются. Кроме того, были известны барионы из трех
тождественных кварков – uuu (Δ++-резонанс),
ddd (Δ-‑резонанс),
sss (Ω--гиперон), в которых
кварки находились в одинаковых квантовых состояниях, что противоречило принципу
Паули. Все эти трудности начального варианта кварковой модели снимались
введением для кварков еще одного квантового числа, названного цветом. Это
квантовое число должно было иметь три возможных значения с тем, чтобы можно было
восстановить принцип Паули для барионов, построенных из трех кварков одинакового
аромата. Эти три возможных значения цвета – красный (к), зеленый (з)
и синий (с) – можно рассматривать как три проекции своеобразного
цветового спина в трехмерном цветовом пространстве (с осями К,
З. С).
С введением цвета Δ++-резонанс, например, можно представить как
комбинацию трех u-кварков в разных цветовых состояниях: Δ++ = uкuзuс. Это означало, что
принцип Паули справедлив и в физике адронов. Однако, ограничиться только
трехзначностью цвета было невозможно. Оставалась ещё одна проблема. Если uкuзuс
- это
единственный вариант Δ++‑резонанса, то для
протона можно предложить несколько кандидатов, не нарушая принципа Паули: uкuзdс,
uкuзdз,
uсuкdк и т. д. Но существует только одно
протонное состояние и введение нового квантового числа «цвет» не должно
увеличивать число наблюдаемых состояний.
Выходом из этой ситуации явилось принятие постулата о бесцветности наблюдаемых квантовых состояний адронов. Бесцветность
адронов означает, что в них кварки разного цвета представлены с равными весами.
О таких бесцветных состояниях говорят как о цветовых
синглетах. Они инвариантны относительно преобразований в трехмерном цветовом
пространстве. Если цветовой индекс кварка принимает три значения α = 1, 2, 3, то такие преобразования имеют вид

при
условии ортонормированности цветовых состояний

где
(*) означает комплексное сопряжение, а δβγ − символ Кронекера.
В отличие от цветных кварков, их наблюдаемые комбинации
− адроны
− всегда бесцветны. В
них все кварковые цвета представлены с одинаковыми весами. В этом состоит
аналогия между цветом в оптике ик вантовым числом цвет. В обоих случаях
равномерная смесь трёх базовых цветов дает бесцветную (белую) комбинацию.
Рассмотрим вопрос о том, как цветовые степени свободы
кварков должны быть учтены в волновых функциях адронов
Y. Поскольку эти степени свободы не зависят от других кварковых степеней
свободы – пространственных координат, спина и аромата, то цветовая часть полной
волновой функции адрона может быть выделена в виде множителя ψcolor:
Ψ = ψcolorФ,
где Ф − часть волновой функции адрона,
куда входят пространственные (space), спиновые (spin) и ароматовые
(flavor) степени свободы кварков. Установим вид ψcolor. Он различен для
мезонов и барионов.
Кварковая структура мезонов q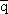 . Для того, чтобы мезон был
бесцветным, все возможные цвета кварка (антикварка) в нём должны быть
представлены с одинаковым весом, что дает цветовую структуру мезона
~ (k . Для того, чтобы мезон был
бесцветным, все возможные цвета кварка (антикварка) в нём должны быть
представлены с одинаковым весом, что дает цветовую структуру мезона
~ (k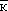 +з +з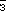 +с +с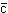 ).
Поэтому, независимо от типа (кваркового состава) мезона цветовая часть его
волновой функции с учетом нормировки имеет вид ).
Поэтому, независимо от типа (кваркового состава) мезона цветовая часть его
волновой функции с учетом нормировки имеет вид

При установлении вида цветовой волновой функции бариона
необходимо учесть принцип Паули. В состав бариона могут входить тождественные
кварки, а, поскольку кварки являются фермионами, то в таких барионах эти кварки
не должны находиться в одинаковых квантовых состояниях. В случае мезонов такого
ограничения нет, так как они содержат только различные частицы
- кварк и антикварк. Это означает, что волновая функция
бариона, содержащего кварки одинакового аромата, должна быть антисимметричной
при перестановке этих кварков.
Рассмотрим ситуацию на примере Δ++-резонанса, состоящего из трёх u-кварков. Его спин-чётность
JP = 3/2+.
Эксперименты показали, что его волновая функция симметрична по пространственным
координатам кварков и не имеет узлов. Следовательно, орбитальный момент кварков
L = 0 и полный момент JP = 3/2 целиком обусловлен спинами кварков,
направленными в одну сторону (↑↑↑). Такое спиновое
состояние симметрично. Следовательно, пространственно-спиново-ароматовая
волновая функция Δ++-резонанса
F симметрична по этим трём переменным. Как показывает
опыт это утверждение справедливо для всех барионов, т. е. все барионы имеют
волновые функции, полностью симметричные к одновременной перестановке
пространственных координат, спинов и ароматов любых двух кварков. Для того
чтобы быть антисимметричной в целом, полная волновая функция
Y любого бариона должна содержать антисимметричную цветовую функцию ψcolor. Нормированная
антисимметричная цветовая волновая функция бариона имеет вид

Такая цветовая функция автоматически обеспечивает выполнение принципа Паули,
запрещающего существование бариона, содержащего кварки одного и того же аромата
в полностью одинаковых квантовых состояних. Ароматово-цветовая волновая
функция Δ++-резонанса
имеет вид

Требуемая антисимметризация волновой функции Δ++-резонанса получена. Она антисимметрична по
цвету, симметрична по пространственным координатам (орбитальные моменты кварков
нулевые) и спинам (↑↑↑). Таким образом, волновая
функция Δ++-резонанса
Y антисимметрична в целом, как и должно быть для систем,
содержащих тождественные фермионы. Легко проверить выполнение принципа Паули для
этого состояния. Пусть зелёный u-кварк стал красным: uз→ uк. Тогда в Δ++‑резонансе имеем два красных u-кварка
в одном и том же состоянии. При этом волновая функция Δ++-резонанса обращается в нуль.
Глюоны – переносчики
сильного цветного взаимодействия
Глюоны – безмассовые электрически нейтральные частицы
со спином J = 1, четностью Р
= -1
- переносят сильное, т. е. цветное
взаимодействие между кварками. Они как бы склеивают кварки в адронах (название
глюона происходит от англ.
glue – клей).
При испускании или поглощении глюона кварки могут изменить свой цвет. При этом
остальные квантовые числа кварка и его аромат не изменяются. Глюоны обладают
цветом. Однако цветовая структура глюона отличается от цветовой структуры
кварка. Её можно установить, используя закон сохранения цвета.
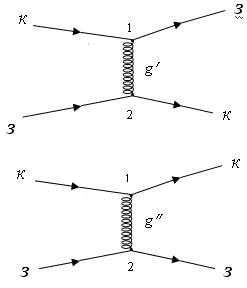
Рис. 11.2.
Варианты сильного взаимодействия красного и зелёного кварков
Рассмотрим сильное взаимодействие двух цветных кварков
- красного (к) и зелёного (з). Могут быть
два варианта этого взаимодействия
– с обменом цветом
(верхняя часть рис. 11.2) и без обмена цветом (нижняя часть рис. 11.2). Будем
считать, что красный кварк испускает глюон (g' или
g") в точке 1, а зелёный его поглощает в
точке 2. Таким образом, понимая под
g' и
g" цветовые заряды (цвета) глюонов, можно, используя
сохранение цвета, записать для верхней диаграммы
точка 1: к
=
g' + з,
точка 2: з +
g' = к,
для нижней диаграммы
точка 1: к
=
g"
+ к,
точка 2: з +
g"
= з.
Откуда получаем цветовую
структуру глюонов
g' и
g":
g' = к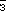 , ,

т. е. глюон обладает
двумя цветовыми признаками – цветом и антицветом. Глюон
g' явно окрашен, а глюон
g" несёт так называемый
скрытый цвет.
Каждый глюон имеет пару цветовых зарядов – цвет и
антицвет. Всего из трех цветов (к, с, з) и трех антицветов
(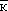 , , 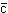 , , 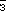 ) можно для глюонов составить
девять возможных парных комбинаций цвет-антицвет: ) можно для глюонов составить
девять возможных парных комбинаций цвет-антицвет:
Парные
комбинации цвет-антицвет
Эти 9 парных комбинаций цвет-антицвет разбиваются на
6 недиагональных явно окрашенных и 3 диагональных, обладающих скрытым цветом: 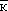 к, к, 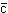 с и с и 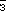 з. Цветовые заряды, как и электрические,
сохраняются. Поэтому 6 недиагональных явно окрашенных пар не смешиваются между
собой. Что касается трёх диагональных пар, то сохранение цветового заряда не
препятствует переходам типа з. Цветовые заряды, как и электрические,
сохраняются. Поэтому 6 недиагональных явно окрашенных пар не смешиваются между
собой. Что касается трёх диагональных пар, то сохранение цветового заряда не
препятствует переходам типа 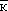 к↔ к↔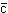 с↔ с↔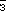 з, т. е. диагональные
пары смешиваются. В результате этих переходов вместо трёх цветовых сочетаний з, т. е. диагональные
пары смешиваются. В результате этих переходов вместо трёх цветовых сочетаний 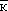 к, к, 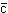 с и с и 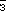 з возникают три других, являющихся их
линейными комбинациями. Стандартные требования симметрии, ортогональности и
нормировки, примененные к глюонным состояниям, позволяют получить вид трёх
недостающих глюонов со скрытым цветом. Три глюона со скрытым цветом представляют
собой следующие цветовые комбинации: з возникают три других, являющихся их
линейными комбинациями. Стандартные требования симметрии, ортогональности и
нормировки, примененные к глюонным состояниям, позволяют получить вид трёх
недостающих глюонов со скрытым цветом. Три глюона со скрытым цветом представляют
собой следующие цветовые комбинации:

Последняя комбинация является симметричной комбинацией
цвета и антицвета. В ней все три цвета и три антицвета смешаны поровну. Такая
лишенная цвета линейная комбинация цветов-антицветов не может играть роль
цветного глюона, реализующего сильное взаимодействие и переносящего цвет от
одного кварка к другому. Таким образом, после исключения комбинации
 остаётся 8 глюонов. остаётся 8 глюонов.
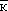 з, з, 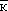 с, с, 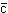 к, к, 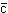 з, з, 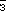 к, к, 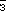 с, с,

Эти
восемь глюонов переносят сильное взаимодействие между кварками.
Так как глюоны обладают цветовым зарядом, то в отличие
от электрически нейтральных фотонов, для них возможны процессы испускания
(поглощения) глюоном глюона (рис. 11.3 а) и рассеяния глюона на глюоне
(рис. 11.3 б).
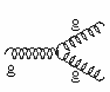
а |
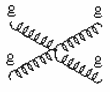
б |
Рис. 11.3. Процессы с участием глюонов.
Взаимодействие глюонов ответственно за удержание
кварков внутри адрона. Особенности этого взаимодействия таковы, что величина
(константа) сильного взаимодействия растет с увеличением расстояния между
кварками.
Экспериментально глюоны наблюдались в виде узких
адронных струй, возникающих при взаимодействии частиц высоких энергий.
Глюоны играют существенную роль в формировании
внутренней структуры адронов. Из процессов глубоконеупругого рассеяния частиц на
нуклонах следует, что примерно половина энергии нуклона приходится на глюоны.
Цветовые заряды кварков являются источниками цветовых
глюонных полей. На этом основании кварки часто называют материей, а глюоны
просто полями. Эта терминология, однако, имеет ограниченный смысл: цветные
заряды глюонов также могут быть источниками глюонов и кварков. Глюон
электрически нейтрален. Поэтому он может порождать кварки только парами –
кварк-антикварк.
Асимптотическая свобода – свойство некоторых моделей сильного взаимодействия,
заключающееся в том, что интенсивность взаимодействия двух кварков в адроне,
характеризуемая эффективной константой взаимодействия αs стремится к нулю с увеличением
переданного импульса Q

где
n – число типов
(ароматов) кварков, Λ – размерный параметр сильного
взаимодействия, экспериментальное значение которого Λ ~100–200 МэВ/с.
То есть при сближении кварки ведут себя как свободные,
невзаимодействующие частицы. Асимптотическая свобода лежит в основе моделей
Великого объединения взаимодействий. Константа сильного взаимодействия
уменьшается до ≈ 1.5 при |Q2| > |1015 ГэВ/с|2 . Свойство
асимптотической свободы ярко проявляется в глубоко неупругих процессах в
приближенном скейлинге Бьёркена.
Нобелевская премия по физике
2004 г. – Д. Гросс,
Д. Политцер,
Ф. Вилчек. За
открытие асимптотическое свободы в теории сильных взаимодействий.

Д. Гросс
(р. 1941) |

Д. Политцер
(р. 1949) |

Ф. Вилчек
(р. 1951) |
[*]
Вильчек Ф.А. «Асимптотическая свобода: от парадоксов
к парадигмам» УФН 175 1325 (2005)
  

|
![]()
![]()
![]() (антибарионы) и q
(антибарионы) и q![]() (мезоны). Однако
оставалось неясным, почему других комбинаций кварков, например, qq,
(мезоны). Однако
оставалось неясным, почему других комбинаций кварков, например, qq,
![]()
![]() , qq
, qq![]() , q
, q![]()
![]() ,
qqqq, qq
,
qqqq, qq![]()
![]() , q
, q![]()
![]()
![]() и т.д. в природе нет, да и сами
отдельные кварки не наблюдаются. Кроме того, были известны барионы из трех
тождественных кварков – uuu (Δ++-резонанс),
ddd (Δ-‑резонанс),
sss (Ω--гиперон), в которых
кварки находились в одинаковых квантовых состояниях, что противоречило принципу
Паули. Все эти трудности начального варианта кварковой модели снимались
введением для кварков еще одного квантового числа, названного цветом. Это
квантовое число должно было иметь три возможных значения с тем, чтобы можно было
восстановить принцип Паули для барионов, построенных из трех кварков одинакового
аромата. Эти три возможных значения цвета – красный (к), зеленый (з)
и синий (с) – можно рассматривать как три проекции своеобразного
цветового спина в трехмерном цветовом пространстве (с осями К,
З. С).
и т.д. в природе нет, да и сами
отдельные кварки не наблюдаются. Кроме того, были известны барионы из трех
тождественных кварков – uuu (Δ++-резонанс),
ddd (Δ-‑резонанс),
sss (Ω--гиперон), в которых
кварки находились в одинаковых квантовых состояниях, что противоречило принципу
Паули. Все эти трудности начального варианта кварковой модели снимались
введением для кварков еще одного квантового числа, названного цветом. Это
квантовое число должно было иметь три возможных значения с тем, чтобы можно было
восстановить принцип Паули для барионов, построенных из трех кварков одинакового
аромата. Эти три возможных значения цвета – красный (к), зеленый (з)
и синий (с) – можно рассматривать как три проекции своеобразного
цветового спина в трехмерном цветовом пространстве (с осями К,
З. С). 
![]()
![]() . Для того, чтобы мезон был
бесцветным, все возможные цвета кварка (антикварка) в нём должны быть
представлены с одинаковым весом, что дает цветовую структуру мезона
~ (k
. Для того, чтобы мезон был
бесцветным, все возможные цвета кварка (антикварка) в нём должны быть
представлены с одинаковым весом, что дает цветовую структуру мезона
~ (k![]() +з
+з![]() +с
+с![]() ).
Поэтому, независимо от типа (кваркового состава) мезона цветовая часть его
волновой функции с учетом нормировки имеет вид
).
Поэтому, независимо от типа (кваркового состава) мезона цветовая часть его
волновой функции с учетом нормировки имеет вид![]()
![]()
![]()

![]() ,
,
![]()
![]() ,
, ![]() ,
, ![]() ) можно для глюонов составить
девять возможных парных комбинаций цвет-антицвет:
) можно для глюонов составить
девять возможных парных комбинаций цвет-антицвет:![]() к,
к, ![]() с и
с и ![]() з. Цветовые заряды, как и электрические,
сохраняются. Поэтому 6 недиагональных явно окрашенных пар не смешиваются между
собой. Что касается трёх диагональных пар, то сохранение цветового заряда не
препятствует переходам типа
з. Цветовые заряды, как и электрические,
сохраняются. Поэтому 6 недиагональных явно окрашенных пар не смешиваются между
собой. Что касается трёх диагональных пар, то сохранение цветового заряда не
препятствует переходам типа ![]() к↔
к↔![]() с↔
с↔![]() з, т. е. диагональные
пары смешиваются. В результате этих переходов вместо трёх цветовых сочетаний
з, т. е. диагональные
пары смешиваются. В результате этих переходов вместо трёх цветовых сочетаний ![]() к,
к, ![]() с и
с и ![]() з возникают три других, являющихся их
линейными комбинациями. Стандартные требования симметрии, ортогональности и
нормировки, примененные к глюонным состояниям, позволяют получить вид трёх
недостающих глюонов со скрытым цветом. Три глюона со скрытым цветом представляют
собой следующие цветовые комбинации:
з возникают три других, являющихся их
линейными комбинациями. Стандартные требования симметрии, ортогональности и
нормировки, примененные к глюонным состояниям, позволяют получить вид трёх
недостающих глюонов со скрытым цветом. Три глюона со скрытым цветом представляют
собой следующие цветовые комбинации:![]()
![]() остаётся 8 глюонов.
остаётся 8 глюонов.
![]() з,
з, ![]() с,
с, ![]() к,
к, ![]() з,
з, ![]() к,
к, ![]() с,
с,
![]()






