Электромагнитные взаимодействия

Электромагнитное взаимодействие является одним из четырех типов фундаментальных взаимодействий:

Переносчиком электромагнитного взаимодействия является квант электромагнитного поля – фотон. Радиус действия сил R и масса переносчика взаимодействия m связаны соотношением

Так как фотон имеет нулевую массу, радиус действия электромагнитных сил бесконечный. Поэтому к электромагнитному взаимодействию сводится большинство явлений, наблюдаемых в макроскопических масштабах – силы трения, упругости и другие. Безразмерная константа

определяет интенсивность электромагнитного взаимодействия.

Фундаментальная вершина электромагнитного взаимодействия

Процессы квантовой электродинамики описываются с помощью одной фундаментальной вершины состоящей из двух фермионных линий ƒ и одной фотонной γ (рис. 4.1)

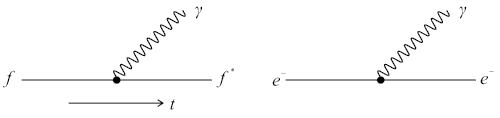
Рис. 4.1. Фундаментальная вершина, описывающая виртуальный процесс испускания фермионом (электроном) фотона.

Вершина электромагнитного взаимодействия описывает виртуальный процесс испускания фермионом, например, электроном фотона (рис. 4.1). Этот процесс является виртуальным, т.к. свободный электрон ни испустить, ни поглотить фотон не может, что можно показать, воспользовавшись равноправием инерциальный систем координат и рассмотрев процесс в системе координат, в которой электрон покоится после поглощения фотона (рис. 4.2). Из законов сохранения энергии и импульса следует = , т. к. до поглощения импульс фотона равен импульсу фотона . После поглощения фотона электроном из закона сохранения энергии следует

(c²p² + m²c⁴)^1/2 + |k|c = mc².

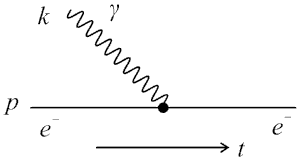
Рис. 4.2. Виртуальный процесс поглощения электроном фотона.

Законы сохранения энергии и импульса могут может выполняться только в том случае, если p = k = 0, т.е. в случае отсутствия фотона. В зависимости от ориентаций фермионных и фотонных линий относительно оси времени основной узел квантовой электродинамики описывает различные виртуальные процессы взаимодействия электронов, позитронов и фотонов.
В приведенных ниже виртуальных процессах (рис. 4.3–4.9) ось времени направлена слева направо.

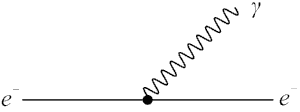
Рис.4.3. Виртуальный процесс испускания электроном фотона

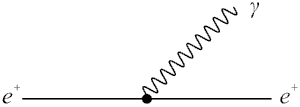
Рис. 4.4. Виртуальный процесс испускания фотона позитроном. Позитрон распространяется по оси времени в противоположном направлении.

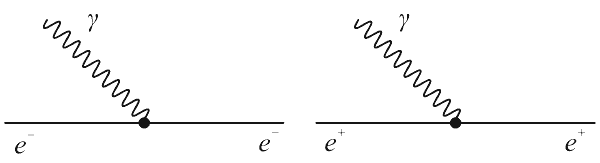
Рис. 4.5. Виртуальные процессы поглощения фотона электроном (слева) позитроном (справа).

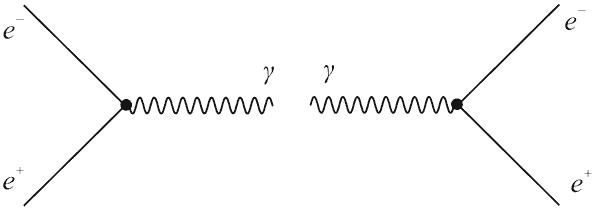
Рис. 4.6. Виртуальные процессы e⁺e^--аннигиляции (слева), образования пары электрон-позитрон (справа).

Образование e⁺e^--пар

Релятивистское обобщение Дираком теории электрона привело не только к предсказанию позитрона, но и к предсказанию того, что при достаточно высоких энергиях E > 1 МэВ возможен процесс образования электрон-позитронных пар. Этот процесс был экспериментально обнаружен в 1932 г.
Во всех процессах, происходящих в Природе, выполняется закон сохранения электрического заряда. Электрону приписывается электрический заряд Q = -1, протону − Q = +1, фотону и другим нейтральным частицам приписывается величины электрического заряда Q = 0. Позитрон, являющийся античастицей по отношению к электрону имеет электрический заряд Q = -1.

Закон сохранения электрического заряда

Квантовое число суммарного электрического заряда не изменяется во всех типах взаимодействий. Сумма всех квантовых чисел электрического заряда частиц после взаимодействия равна их сумме до взаимодействия.

Закон сохранения электрического заряда не запрещает изменение числа заряженных частиц. В результате аннигиляции электрона и позитрона число заряженных частиц уменьшается на две единицы. При этом суммарный электрический заряд остаётся равным нулю, как до взаимодействия, так и после взаимодействия. Процесс рождения электрон-позитронной пары подчиняется тому же закону сохранения электрического заряда. Любая частица может быть рождена или уничтожена одновременно со своей античастицей. При этом все квантовые числа будут автоматически сохраняться.
Из законов сохранения импульса и энергии следует, что процесс образования электрон-позитронных пар не может происходить в вакууме. Процесс образования пар происходит лишь в кулоновском поле третьей частицы, получающей часть импульса и энергии. Процесс рождения фотоном электрон-позитронной пары в поле атомного ядра Z показан на рис. 4.7.

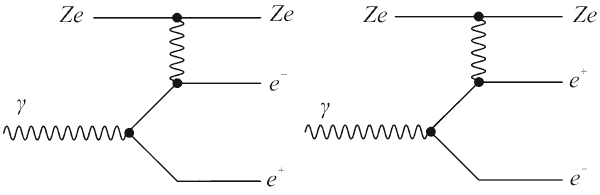
Рис. 4.7. Образование e⁺e^--пары в кулоновском поле атомного ядра.

В более компактном виде диаграмму Фейнмана образования электрон-позитронной пары в кулоновском поле атомного ядра можно изобразить в виде, показанном на рис. 4.8.

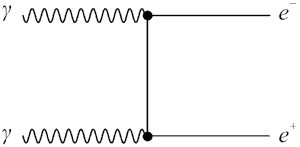
Рис. 4.8. Образование e⁺e^--пары в кулоновском поле атомного ядра.

Диаграмма Фейнмана рассеяния фотона на фотоне имеет вид.

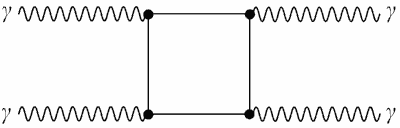
Рис. 4.9. Диаграмма Фейнмана рассеяния фотона на фотоне.

Образование e⁺e^--пар в поле атомного ядра происходит в случае, если энергия γ-кванта удовлетворяет соотношению

E_γ ≥ 2m_ec² + E_n,

где первый член соответствует энергии покоя пары электрон и позитрон, а второй − энергии отдачи ядра. Так как энергия отдачи ядра сравнительно мала, то энергия, определяемая первым членом, является порогом рождения пар (2m_ec² 1.022 МэВ). Одиночный квант любой энергии не может превратиться в электрон-позитронную пару, т.к. при этом не выполняются одновременно законы сохранения энергии и импульса. В основном образование e⁺e^--пар происходит в кулоновском поле ядер атомов. Эффективное сечение этого процесса пропорционально квадрату заряда ядра Z². Электрон-позитронные пары также могут образовываться в кулоновском поле электрона.
В этом случае порог рождения e⁺e^--пар в поле электрона равен 4m_ec². Увеличение порога рождения e⁺e^--пар в кулоновском поле электрона связано с тем, что энергию отдачи получает электрон, имеющий малую массу, и пренебречь ею уже нельзя. Образование пар в поле электрона имеет сравнительно малую вероятность. На рис. 4.10 показана зависимость сечений образования e⁺e^-‑пар на протоне и электроне в области энергий до 100 МэВ. С увеличением энергии γ-кванта разность сечений убывает.

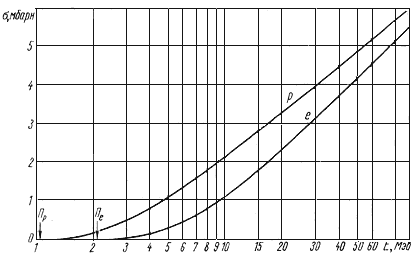
Рис. 4.10. Эффективные сечения образования электронно-позитронных пар γ-квантами с энергией ≤100 МэВ на протоне и электроне.

На рис. 4.11 приведено теоретически рассчитанное эффективное сечение образования электронно-позитронных пар γ-квантами на протоне, атомах водорода и свинца в области энергий до 10⁶ МэВ.

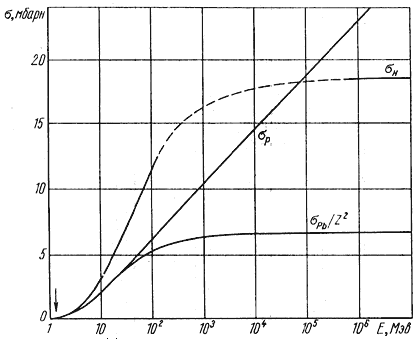
Рис. 4.11. Эффективное сечение образования электронно-позитронных пар γ-квантами большой энергии на протоне σ_p и атомах водорода σ_H и свинца σ_Pb.

На рис. 4.12 показана вероятность P образования фотоном e⁺e^-‑пар в веществе с различным зарядом ядер. Видно, что вероятность образования электрон-позитронной пары растет с ростом энергии фотона и увеличением заряда ядра и достигает предельного значения в области нескольких сотен МэВ.

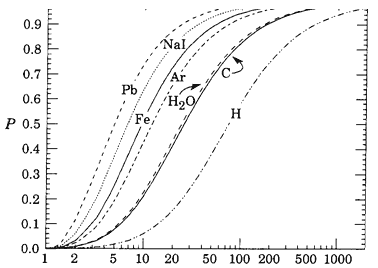
Энергия γ-кванта (МэВ)

Рис. 4.12. Зависимость вероятности образования электрон-позитронной пары в кулоновском поле атомного ядра от заряда атомного ядра и энергии фотона.

При образовании e⁺e^--пары часть энергии γ-кванта E превращается в энергию покоя пары частиц 2m_ec², а оставшаяся энергия E − 2m_ec² переходит в кинетические энергии трех частиц: электрона e^-, позитрона e⁺ и атомного ядра (или электрона), в поле которого происходит образование пары. Распределение кинетической энергии между этими тремя частицами зависит от масс частиц и углов их разлёта. Поэтому энергия частиц не определяется однозначно направлением вылета частиц, а имеет непрерывное распределение от нулевой до максимальной E − 2m_ec². Максимальная энергия позитрона или электрона при образовании пар на атомных ядрах близка к энергии E − 2m_ec², т. к. масса ядра велика по сравнению с массами электрона и позитрона m_e, а энергия отдачи ядра мала.
На рис. 4.13 показаны теоретически рассчитанные спектры электронов (позитронов) при образовании e⁺e^-‑пар γ‑квантами различных энергий. Угловое распределение позитронов и электронов зависит от энергии γ-кванта E. Если E >> 2m_ec² импульс образовавшейся e⁺e^-‑пары близок по величине и направлению к импульсу γ-кванта, т.е. электрон и позитрон летят в том же направлении, что и образовавший их γ-квант, с малым относительным углом разлёта электрона и позитрона. Средний угол вылета частиц θ имеет величину

θ ≈ m_ec²/E.

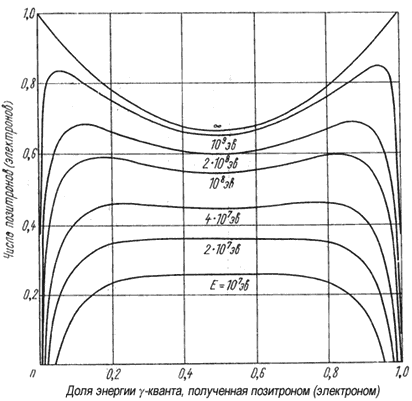
Рис. 4.13. Теоретически рассчитанные спектры позитронов (электронов) при образовании пар γ-квантами различной энергии E/m_ec² в воздухе.

В природных условиях образование e⁺e^-‑пар происходит при взаимодействии космических лучей с веществом. Распады положительно и отрицательно заряженных мюонов

μ^- → e^- + _e + ν_μ,
μ⁺ → e⁺ + ν_e + _μ,

составляющие сильно проникающую компоненту космического излучения, и распады π⁰-мезонов

π⁰ → 2γ

приводят к образованию каскадных ливней и размножению числа e⁺e^-‑пар.
Образование e⁺e^--пар эффективно происходит в звездах, когда температура повышается выше 10⁹ К. Взаимодействие электронов и позитронов с атомными ядрами приводит к образованию химических элементов в звездах и, в частности, к образованию химических элементов в районе железного максимума. Образование и последующая аннигиляция e⁺e^-‑пар

γ → e⁺e^- → ν

имеют большое значение в механизме испускания нейтрино в звездах и влияют на эволюцию звезд. Аннигиляция электрон-позитронных пар с образованием пары ν приводит к заметной потере энергии в звездах.

e⁺e^--аннигиляция. Низкие энергии

Одним из ярких свойств взаимодействия частиц и античастиц является процесс аннигиляции. Аннигиляция − это процесс, в котором частица и соответствующая ей античастица превращаются в кванты электромагнитного поля или в другие частицы − кванты физических полей другой природы. Характер продуктов аннигиляции и соотношение вероятностей различных каналов аннигиляции определяются типом взаимодействия и правилами отбора, вытекающими из закона сохранения. Например, при соударении электрона и позитрона они оба могут исчезнуть, образовав два фотона:

e⁺ + e^- → 2γ.

При достаточно высокой энергии электрон-позитронная пара может превратиться в совокупность тяжелых частиц − адронов, например, возможен процесс образования пары протон–антипротон

e⁺ + e^- → p + .

    Для того чтобы была возможна аннигиляция пары e⁺e^- с образованием протона и антипротона, полная суммарная энергии пары электрон–позитрон в системе центра масс должна быть больше, чем суммарная масса протона и антипротона, т. е. больше (2×940) МэВ.
    Процесс аннигиляции при низких энергиях E < m_μc² ниже порога рождения наиболее лёгких заряженных лептонов μ⁺μ^-‑мюонов приводит к единственному процессу − рождению γ-квантов. Основным процессом при этих энергиях будет двухфотонная аннигиляция.
    Попав в вещество, позитрон испытывает большое количество столкновений с атомами вещества и быстро теряет энергию на их ионизацию. Сечение двухфотонной аннигиляции для свободного электрона и позитрона, движущихся с относительной скоростью v << c, вычисленное Дираком, описывается следующей зависимостью от скорости позитрона v:

где r₀ − классический радиус электрона, а скорость v выражена в см/с. Вероятность аннигиляции позитрона λ небольшой энергии в среде с плотностью электронов N_e определяется соотношением

λ = N_eσv = N_eπr₀²c = 0.7·10^-14

Время жизни позитрона τ в конденсированной среде N_e = 10²⁴ см^–3

τ = 10^-10 с.

В межзвездной среде N_e = 1 см^–3 время жизни медленного позитрона относительно аннигиляции

τ = 10¹⁴ с ≈ 3·10⁶ лет.

Сечение аннигиляции быстро падает с увеличением относительной скорости сталкивающихся частиц. Поэтому в подавляющем большинстве случаев аннигиляция происходит после того, как позитрон потеряет всю свою энергию на ионизацию, т. е. при v ≈ 0. Следовательно, относительный момент e⁺e^--пары l = 0 и e⁺e^--аннигиляция будет происходить в S‑состоянии.
Рассмотрим, как влияют законы сохранения на процесс двухфотонной аннигиляции остановившегося позитрона. Из закона сохранения энергии следует

m₊c² + m_-c² = Eγ₁ + Eγ₂,

где m₊, m_- − масса соответственно позитрона и электрона (m₊c² + m_-c² = 0.511 МэВ), Eγ₁₂ − энергии образовавшихся фотонов. Из закона сохранения импульса следует

0 = P₊ + P_- = Pγ₁ + Pγ₂.

Выполнение законов сохранения энергии и импульса приводит к тому, что рождающиеся в двухфотонной аннигиляции γ-кванты имеют одинаковые энергии:

Eγ₁ = Eγ₂ =m_ec²

и разлетаются в противоположных направлениях.
В том случае, когда аннигилирует движущийся позитрон (v ≠ 0), угол разлета фотонов и распределение энергии между фотонами зависят от скорости позитрона. При больших энергиях ε аннигилирующих позитронов (ε >> m_ec²) фотоны испускаются преимущественно вперед и назад относительно направления движения позитронов. Фотон, летящий вперед, уносит почти всю энергию позитрона, на долю же фотона, летящего назад, остается энергия, примерно равная половине энергии покоя электрона m_ec²/2. На аннигиляции ускоренных пучков позитронов основан метод получения квазимонохроматических γ-квантов высокой энергии.
Векторная диаграмма импульсов фотонов в случае трехфотонной аннигиляции показана на рис. 4.14.

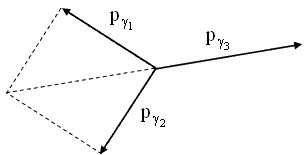
Рис. 4.14. Векторная диаграмма импульсов фотонов в случае трёхфотонной аннигиляции.

Суммарный момент J, уносимый фотонами в случае двухфотонной и трехфотонной аннигиляции может иметь значение J = 0 или J = 1 в зависимости от направлений спинов e⁺e^--пары (рис. 4.15).

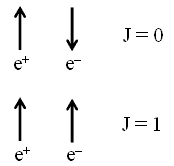
Рис. 4.15. Возможные значения полного спина J системы e⁺e^- при аннигиляции в S‑состоянии.

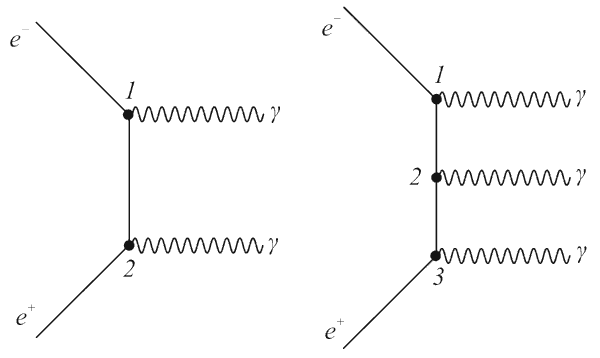
Рис. 4.16. Процесс аннигиляции пары e⁺e^-: а) двухфотонная аннигиляция; б) трехфотонная аннигиляция.

Процесс аннигиляции пары e⁺e^- изображается диаграммами, показанными на рис. 4.16. Процесс двухфотонной аннигиляции показан на рис. 4.16а. На рис. 4.16б показан процесс испускания трех фотонов. На рисунке ось времени направлена слева направо. Каждой частице на диаграмме Фейнмана соответствует определенная линия. Сплошные линии описывают электрон и позитрон, волнистые − фотоны. Свободные концы линий соответствуют невзаимодействующим частицам в начальном и конечном состояниях. Взаимодействие частиц на диаграммах описывается вершинами (точки 1, 2, 3 на рис. 4.16) и рассматривается как испускание и поглощение различных виртуальных частиц. Виртуальным частицам соответствуют внутренние линии, соединяющие вершины. На диаграмме рис. 4.16а в точке 1 электрон превратился в фотон и виртуальную частицу, которая затем в точке 2 поглощается позитроном. Вершине сопоставляется константа связи, характеризующая интенсивность взаимодействия. В случае электромагнитных взаимодействий константа равна

α^1/2 = (e²/ћc)^1/2.

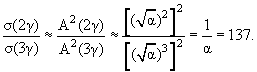
Амплитуда процесса пропорциональна константе связи в степени равной числу вершин в диаграмме Фейнмана. Диаграмме с N вершинами соответствует амплитуда A, пропорциональная α^N/2. Эффективное сечение процесса определяется квадратом амплитуды. Оно будет, таким образом, пропорционально α^N. Так как для электромагнитного взаимодействия α << 1 наибольший вклад дают диаграммы с минимальным числом вершин. Поэтому, не проводя расчетов, можно оценить соотношение вероятностей различных процессов. Так, например, для процессов, изображенных на рис. 4.16, сечение двухфотонной аннигиляции примерно на два порядка больше сечения трехфотонной аннигиляции

    Таким образом, для электромагнитных процессов каждая дополнительная вершина соответствует подавлению процесса примерно на 2 порядка. Поэтому трехфотонная аннигиляция должна происходить гораздо реже, чем двухфотонная. Эксперименты показывают, что из каждой тысячи аннигилирующих позитронов, лишь единицы аннигилируют с образованием трёх фотонов.
    Характерное время жизни позитронов в веществе ~10^–10c.
    Если позитрон находится в веществе, в результате взаимодействия позитрона с электронами и ядрами среды позитрон постепенно теряет энергию до тех пор, пока его энергия не уменьшится настолько, что он термализуется в среде. В результате взаимодействия с электроном среды позитрон до того как произойдет e⁺e^--аннигиляция может образовать связанное состояние − позитроний. Поэтому аннигиляция часто идет через образование связного состояния системы e⁺e^--позитрония. Позитроний, в котором спины электрона и позитрона антипараллельны (парапозитроний) имеет время жизни 1.2·10^-10 с и распадается на 2 γ-кванта. Позитроний, в котором спины электрона и позитрона параллельны (ортопозитроний) распадается на 3 γ‑кванта и имеет среднее время жизни 1.4·10^-7 с. Более подробно см. п. 7 и 17.

Электромагнитные взаимодействия в e⁺e^--соударениях

Исследованиеe⁺e^--столкновений является эффективным средством изучения электромагнитных взаимодействий лептонов. Электромагнитные взаимодействия с участием лептонов при энергиях в системе центра масс E_ц.м. = 0.5 ГэВ представлены в основном следующими процессами:

e^-e^- → e^-e^-;
e⁺e^- → γγ;
e⁺e^- → e⁺e^-;
e⁺e^- → μ⁺μ^-.

Реакции e^-e^- → e^-e^-, e⁺e^- → e⁺e^- и e⁺e^- → γγ происходят во всём диапазоне энергий E_ц.м. сталкивающихся частиц. Рождение μ⁺μ^--пар возможно при энергии E_ц.м. выше 214 МэВ (энергия покоя мюона m_μc² = 107 МэВ). Дифференциальные сечения реакций при энергии E_ц.м. = 1 ГэВ приведены на рис. 4.17.

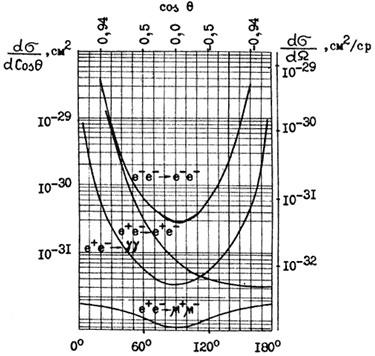
Рис. 4.17. Дифференциальные сечения реакций e^-e^- → e^-e^-, e⁺e^- → e⁺e^- и e⁺e^- → γγ, e⁺e^- → μ⁺μ^- при E_ц.м. = 1 ГэВ.

Характерной особенностью электромагнитных взаимодействий лептонов при высоких энергиях является сильная угловая зависимость продуктов реакции от направления сталкивающихся частиц. Продукты реакции вылетают в направлении сталкивающихся частиц. Большая часть их вылетает в пределах угла θ ≈ mc²/E, где m − масса продуктов реакции, E − энергия столкновения. Зависимость формы угловых распределений от массы частиц в конечном состоянии отчетливо проявляется при сравнении угловых распределений реакций e⁺e^- → e⁺e^- и e⁺e^- → μ⁺μ^-.

4. Электромагнитные взаимодействия

Фундаментальная вершина электромагнитного взаимодействия

Образование e+e--пар

e+e--аннигиляция. Низкие энергии

Электромагнитные взаимодействия в e+e--соударениях

Образование e⁺e^--пар

e⁺e^--аннигиляция. Низкие энергии

Электромагнитные взаимодействия в e⁺e^--соударениях