Рождение W и Z в паре с фотоном

    Интегральные и дифференциальные сечения рождения Wи Z бозонов в паре с фотоном высокой энергии измерены в эксперименте ATLAS на интегральной светимости 4.6 фб^-1, накопленной для рр соударений при 7 ТэВ [1]. Отбирались события с лептонными каналами распада W(eν, μν) и Z (e⁺e⁻, μ⁺μ⁻, νν) и ассоциированным рождением изолированного фотона высокой энергии. Такие события позволяют провести проверку электрослабого сектора Стандартной модели  и могут быть использованы для поиска новых явлений. С помощью этих измерений установлены новые ограничения на константы аномальных трех-бозонных вершин WWγ, ZZγ и Zγγ (аTGC) и проведен поиск векторных резонансов, распадающихся на Wγ и Zγ.
    Взаимодействия W и Z бозонов с фотонами представляют интерес для проверки самодействия этих бозонов в соответствии с предсказаниями неабелевой SU(2)_L×U(1)_Y  группы электрослабого сектора Стандартной модели. Особый интерес измерения Wγ и Zγ рождения представляют для новой энергетической области, достигнутой на БАК. Они позволяют, в частности, провести поиск технимезонов, предсказанных моделью техницвета [2,3].
    Конечные состояния пар бозонов рождаются в реакциях рр → ℓνγ + Х, рр → ℓ⁺ℓ^-γ + Х и
рр → ννγ + Х. Эти состояния включают рождение W и Z с фотоном от излучения заряженным лептоном от W/Z распадов в дополнение к состояниям Wγ и Zγ, представляющих интерес для анализа. В СМ последние составляю рождение W и Z вместе с фотонами от излучения начальных кварков (прямые фотоны), от фрагментации вторичных кварков и глюонов в изолированные фотоны и от непосредственного излучения фотона W бозонами. Диаграммы этих процессов приведены на рис.14.1.

 
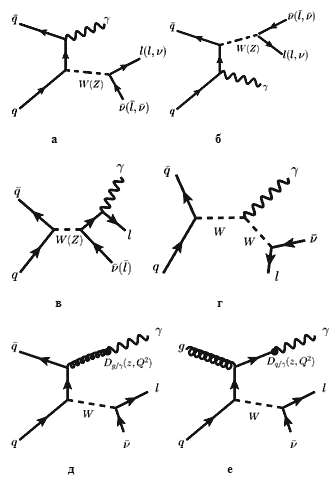
Рис.14.1. Фейнмановские диаграммы Wγ и Zγ рождения в u-канале (а), t-канале (б), излучение фотона в конечном состоянии ( FSR) – (в); (г) – фейнмановская диаграмма рождения Wγ в s-канале. Диаграммы вклада в сигнал от W+q(g) процессов, когда фотон испускается при фрагментации глюона (д) и кварка (е) в конечном состоянии.

    Кандидаты  ℓνγ отбирались по наличию лептона с р_Т > 25 ГэВ/с и фотона с Е_Т^γ> 15 ГэВ и недостающей энергии Е_Т^нед > 35 ГэВ. Поперечная масса системы лептон- Е_Т^нед (m_T) удовлетворяла условию m_T > 40 ГэВ. Накладывалось вето на пары еγ в канале с рождением электрона с массой m_еγ в области массы Z бозона (±15 ГэВ).
    Кандидаты канала ℓ⁺ℓ^-γ имели лептоны одного типа с противоположными зарядами и с массой m_ℓℓ > 40 ГэВ и  один изолированный фотон с Е_Т^γ> 15 ГэВ.
        Кандидаты ννγ соответствовали условиям наличия одного изолированного фотона с
Е_Т^γ> 100 ГэВ и величиной недостающей энергии Е_Т^нед> 90 ГэВ. Реконструированные фотон, Е_Т^нед и струи (если присутствуют) должны быть хорошо разделены по азимутальному углу с Δφ
(Е_Т^нед, γ) > 2.6 и Δφ (Е_Т^нед, jet) > 0.4 для уменьшения фона от γ + jet событий.
    Для анализа Wγ и Zγ конечных состояний требовалось также условие разделения лептона и фотона ΔR(ℓ, γ) > 0.7для подавления вкладов от излучения фотона в распадах W и Z. События без струй с
Е_Т > 30 ГэВ использовались для измерения эксклюзивного сечения Wγ и Zγ рождения (Vγ). События с фотонами высокой энергии имеют большее число струй. Вклад аномальных трех-бозонных вершин также увеличивают выход фотонов большой энергии. Ожидается, что эксклюзивное рождение окажется более чувствительно к проявлению вклада аTGC, чем инклюзивные события. Действительно, как показал анализ, эта чувствительность в эксклюзивных каналах оказалась выше на ~40%, чем в инклюзивных.
    В измерениях учитывались стабильные частицы, т.е. с временем жизни более 19 пс, рожденные в жестком рассеянии или после процесса адронизации, но до взаимодействия в детекторе. Полные сечения рассматриваемых реакций приведены к расширенной кинематической области, определенной в таблице 1, а сами сечения содержатся в таблице 2.

 
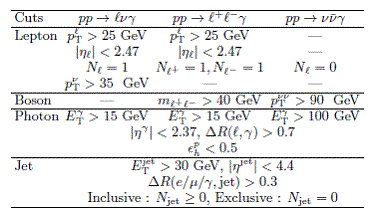
Таблица 1. Определение расширенных областей переменных, для которых получены значения полных сечений реакций. Переменная р_Т^ν обозначает поперечный импульс нейтрино от распада W, р_Т^νν – поперечный импульс Z бозона, распавшегося на два нейтрино ν и , N_ℓ – число лептонов в одном событии, ε^γ_h – параметр изолированности фотона (энергия на уровне частиц в конусе ΔR < 0.4 вокруг направления фотона, отнесенная к его энергии).

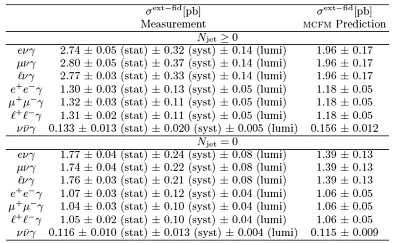
Таблица 2. Измеренные сечения для процессов рр → ℓνγ + Х, рр → ℓ⁺ℓ^-γ + Х и рр → ννγ + Х при энергии соударения протонов 7 ТэВ в пикобарнах для области переменных, определенной в таблице 1, вместе с предсказаниями СМ, полученных с помощью генератора MCFM, рассчитанных на уровне NLO (J.M.Campbell, R.Ellis and C.Williams, JHEP 1107, 018 (2011)).

    Дифференциальные сечения дают более детальное сравнение с теоретическими предсказаниями, позволяя сравнивать не только количество событий, но и форму распределений. На рис.14.2 показано дифференциальное сечение как функция энергии фотона Е_Т^γ в процессах Vγ для инклюзивной выборки с числом струй N_jet ≥ 0 и эксклюзивной с отсутствием струй в сравнении с предсказаниями СМ. На рис.14.3 приведены распределения отобранных событий  Wγ и Zγ по числу струй в событии для разных пороговых значений энергии фотона Е_Т^γ также в сравнении с предсказаниями СМ. И на рис.14.4 с предсказаниями СМ сравниваются дифференциальные сечения инвариантных масс Wγ  (m_T^Wγ) и Zγ (m^Zγ).

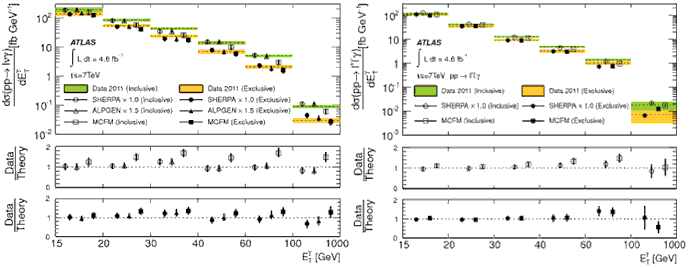
Рис.14.2. Дифференциальные сечения как функция энергии фотона Е_Т^γ в процессах Vγ для инклюзивной выборки (N_jet≥0) и эксклюзивной с отсутствием струй (N_jet=0)  в сравнении с предсказаниями СМ, полученных с помощью генераторов ALPGEN(х1.5), SHERPA и MCFM для конечных состояний ℓνγ − (слева)  и состояний ℓℓγ − (справа).

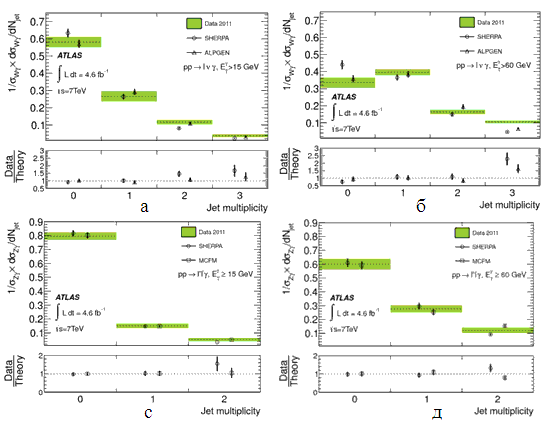
Рис.14.3. Дифференциальные сечения как функция числа струй N_jet в событии для процессов
рр → ℓνγ (а,б) и  рр → ℓ⁺ℓ^-γ (с,д) для событий с энергией фотона Е_Т^γ > 15 ГэВ (а, с) и Е_Т^γ ≥60 ГэВ (а, с) в сравнении с предсказаниями SHERPAи MCFM. Предсказания MCFM для N_jet=2 и 3 для рр → ℓνγ не расчитаны и не приведены.

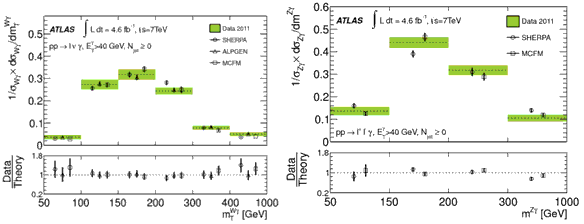
Рис.14.4. Дифференциальные сечения инвариантных масс Wγ  (m_T^Wγ) слева и Zγ (m^Zγ) справа в сравнении с предсказаниями СМ, полученных с помощью генераторов SHERPA и MCFM
(Е_Т^γ> 40 ГэВ, N_jet ≥ 0).

    Расчеты  SHERPA (LO) и MCFM (NLO) для рр → ℓ⁺ℓ^-γ хорошо воспроизводят спектр по Е_Т^γ и числу струй, но распределение по массе m^Zγ несколько лучше описываются расчетами NLOMCFM.
    Для процесса рр → ℓνγ распределения по энергии фотона Е_Т^γ сравниваются с расчетами NLOMCFM и предсказаниями генераторов ALPGEN и SHERPA, но отнормированных на количество событий. Расчеты MCFM согласуются со спектром Е_Т^γ при малых Е_Т^γ, но расходятся для больших Е_Т^γ. Этот эффект лучше проявляется для инклюзивной выборки. Генераторы ALPGEN и SHERPA хорошо описывают форму спектра по Е_Т^γ во всем диапазоне энергий фотонов. Все три расчета хорошо описывают распределение по массе m_T^Wγ  (рис.14.4). Лучшее описание в ALPGEN и SHERPA спектра по Е_Т^γ может быть отнесено за счет процессов с большой множественностью партонов, описываемых древесными диаграммами высокого порядка в константе сильного взаимодействия. Из рис. 3б видно, что вклад событий с большим числом струй более существенен для выборки с фотонами высокой энергии. В расчетах NLO MCFM учитывается испускание только одного реального партона, кварка или глюона. Недостаточный учет КХД процессов более высокого порядка приводит к недооценке предсказываемого сечения. По той же причине улучшенное описание в  ALPGEN по сравнению с SHERPA распределений по множественности струй может быть отнесено на счет того, что в ALPGEN в матричный элемент включено больше  дополнительных жестких партонов.  
    Результаты, полученные в данном анализе для констант aTGCs, приведены на рис.14.5 в сравнении с результатами LEP и Теватрона. Не найдено отклонений от предсказания Стандартной модели.

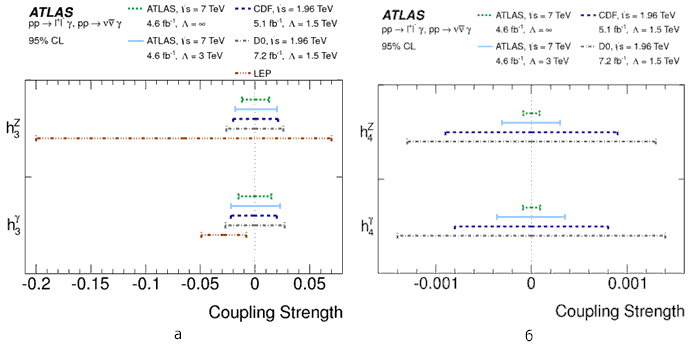
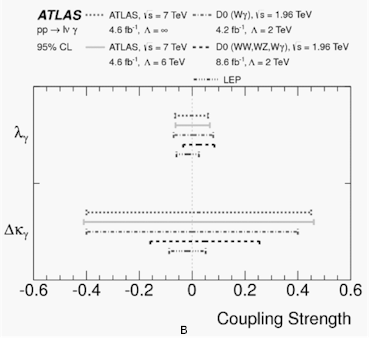
Рис.14.5. Интервалы для констант aTGCs на 95% CL, полученные в эксперименте ATLAS в сравнении с результатами других экспериментов, а,б – для нейтральной aTGC, в – для заряженных aTGCs.  

    Результаты поиска узких резонансов, предсказываемых моделью Техницвета, приведены на рис.14.6. Рождение резонанса α_Т исключено до массы m_αТ = 703 ГэВ в Wγ моде и  резонанса ω_T  до массы m_ωТ = 494 ГэВ в канале Zγ.  

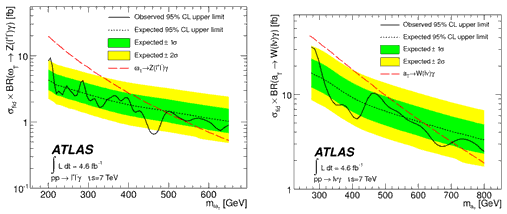
Рис.14.6.  Пределы на рождение узкого векторного резонанса на 95% уровне достоверности в канале рр → ℓνγ (справа) и  рр → ℓ⁺ℓ⁻γ (слева) [1].

Электрослабое рождение Z бозонов и пары струй

    В эксперименте ATLAS измерено электрослабое рождение двух струй совместно с Z бозоном [4]. Для измерений использована полная интегральная светимость для рр соударений при 8 ТэВ
20.3 фб^-1. Электрослабое рождение выделено путем вычитания фона из спектра инвариантных масс пар струй  для инклюзивного парного рождения струй, который происходит за счет сильного взаимодействия. Свидетельство присутствия механизма электрослабого рождения получено на уровне, соответствующим предсказанию Стандартной модели. Гипотеза отсутствия  механизма электрослабого рождения отвергнута данными на уровне 5σ. Электрослабый процесс включает VBF механизм рождения Z бозонов и может быть использован для определения пределов на величину константы связи аномальных трех-бозонных вершин.
        Доминирующим механизмом рождения Z бозона с двумя струями в рр соударениях на БАК является механизм Дрелла-Яна, когда две ассоциированные с  Z струи рождаются за счет сильного взаимодействия. Рождение Zjj через t-канальный обмен электрослабым калибровочным бозоном является  чисто электрослабым процессом и поэтому очень редким. Электрослабое рождение  Zjj с лептонным распадом Z на два мюона или электрона включает все вклады в ℓ⁺ℓ⁻jj  рождения, где происходит t-канальный обмен электрослабым калибровочным бозоном. К ним относятся процессы слияния векторных бозонов VBF,  радиационное испускание Z бозона и нерезонансное  ℓ⁺ℓ^-jj  рождение, диаграммы которых приведены на рис.14.7. Процесс VBF представляет особый интерес, поскольку он дает вклад в рождение бозона Хиггса и дает информацию об аномальной трех-бозонной вершине. Примеры диаграмм рождения Zjj за счет сильного взаимодействия приведены на рис.14.8.

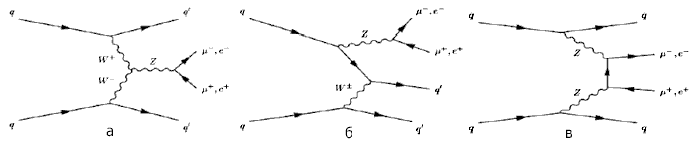
Рис.14.7. Репрезентативный ряд фейнмановских диаграмм лидирующего порядка электрослабого рождения Zjj на БАК: a) слияние векторных бозонов VBF, б) радиационное испускание Z бозона; в) нерезонансное  ℓ⁺ℓ⁻jj  рождение.

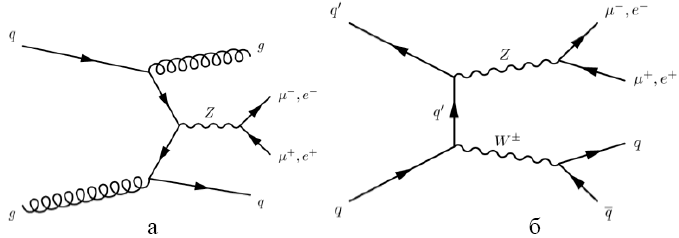
Рис.14.8. Примеры фейнмановских диаграмм лидирующего порядка для рождения Zjj за счет сильного взаимодействия: а) сильное рождение Zjj; б) Zjj рождение за счет рождения пары векторных бозонов.

    Выполнены  измерения сечений и дифференциальных спектров рождения Zjj для  пяти областей фазового пространства с разной чувствительностью к вкладу электрослабого механизма рождения. Инклюзивное рождение  Zjj обусловлено в основном процессами сильного взаимодействия (рис.14.8а). Отсюда следуют ограничения на моделирование КХД процессов, которые приводят к таким же топологиям, что и VBF механизм. Наблюдение электрослабого рождения Zjj и измерение его сечения выполнено для двух кинематических областей. На рис.14.9 приведены дифференциальные спектры по массе двух струй m_jj для варианта выборки событий с Z бозоном и по крайней мере двумя струями с р_Т^j1 > 55 ГэВ/с и p_T^j2 > 45 ГэВ/с. Она содержит все другие выборки, определенные для пяти фазовых объемов. Особо выделена область больших масс струй m_jj > 1 ТэВ и больших поперечных импульсов с Z бозоном и по крайней мере двумя струями с р_Т^j1> 85 ГэВ/с и
p_T^j2 > 75 ГэВ/с. Две последние области используются для выделения электрослабого рождения Zjj, т.к. электрослабый механизм приводит к появлению более жестких струй и больших инвариантных масс m_jj, чем процессы сильного рождения Zjj. На рис.15.9 справа отчетливо видно лучшее согласие расчетов с данными при учете механизма электрослабого рождения.
    Измеренное сечение электрослабого рождения Zjjв распаде Z на два электрона составляет
σ_EW^ee  = 67.2 ± 6.9(стат.)^+12.7_-13.4(сист.) ± 1.9(свет.) фб; в распаде Z на два  мюона
σ_EW^μμ  = 45.6 ± 6.1(стат.)^+9.1_-9.6(сист.) ± 1.3(свет.) фб. Средневзвешенное значение сечения составляет величину σ_EW  = 54.7 ± 4.6(стат.)^+9.8_-10.4(сист.) ± 1.5(свет.) фб. Эта величина может быть сравнена с предсказанием генератора POWHEG для сечения электрослабого рождения Zjj 
σ_EW ^POWHEG  = 46.1 ± 0.2(стат.)^+0.3_-0.2(шкала)±0.8(PDF)±0.5(модель). Наблюдается хорошее согласие расчета с экспериментом.
    Получена величина сечения электрослабого рождения Zjj для области, актуальной для поиска новых явлений с инвариантной массой двух струй m_jj > 1 ТэВ
σ_EW ^{mjj > 1 ТэВ}  = 10.7 ± 0.9(стат.)±0.9(сист.)±0.3(светим.). Она согласуется с аналогичным сечением, предсказанным POWHEG,
σ_EW^{POWHEG,mjj>1ТэВ} = 9.38 ± 0.05(стат.)^+0.15_-0.24(шкала)±0.24(PDF)±0.9(модель).
    Ограничения на константы аномальной трех-бозонной вершины, полученные из измерения электрослабого рождения, примерно в три раза слабее, чем найденные их измерений сечения рождения WZ.

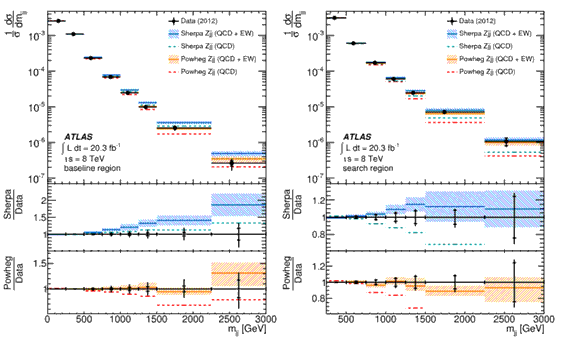
Рис.14.9. Unfolded нормированные распределения по инвариантной массе двух струй для Zjj рождения для основной области, где представлена практически инклюзивная выборка событий, и области поиска с большими значениями массы двух струй m_jj с р_Т^j1> 55 ГэВ/с и p_T^j2> 45 ГэВ/с, где ожидается оптимальный вклад электрослабого рождения, в сравнении с предсказаниями генераторов PYTHIAи SHERPAдля сильного рождения (QCD) и сильного с участием электрослабого (QCD+EW).

Литература к разделу 14

1. Measurement of Wgamma and Zgamma Production in pp collisions at sqrt(s) = 7 TeV with the ATLAS Detector at the LHC, ATLAS Collaboration, Phys. Rev. D 87, 112003 (2013).
2. S.Weinberg, Phys.Rev.D 19, 1277 (1979).
3. L.Susskind, Phys. Rev. D 20, 2619 (1979).
4. Measurement of the electroweak production of dijets in association with a Z-boson and distributions sensitive to vector boson fusion in proton-proton collisions at sqrt(s) = 8 TeV using the ATLAS detector, ATLAS Collaboration, arXiv:1401.7610, subm.to JHEP