Во Внутреннем детекторе и соленоиде реконструируются и измеряются треки заряженных частиц с поперечными импульсами > 0,5 ГэВ/с в интервале псевдобыстрот |η| < 2,5. Эффективность реконструкции при малых р_т ограничена присутствием большого количества вещества в объеме Внутреннего детектора. Для определения разрешения при измерении поперечных импульсов треков использовались отдельные прямо рожденные частицы с р_т выше 1 ГэВ/с и частицы струй. Величины разрешения аппроксимировались выражением

σ_x = σ_x(∞)(1 + px/р_т)

    Оно применимо как для треков с очень большими (бесконечными) импульсами, где разрешение определяется в основном разрешением детекторов (σ_х(∞)), так и для низкоэнергичных треков, где основную погрешность вносит многократное рассеяние в веществе детектора (р_х учитывает реальный р_т трека). В таблице 10.1 величины разрешений (RMS) при значении р_х, когда вклад в разрешение от многократного рассеяния равен вкладу от разрешения детекторов, и для области центральных псевдобыстрот, где эффект вещества минимален, и для передней области с максимальным количеством вещества. Разрешение измерения поперечного импульса и углов получено для треков мюонов в первых трех строках, а разрешение для измерения прицельного параметра приведено для пионов (две нижние строки).

Таблица 10.1.

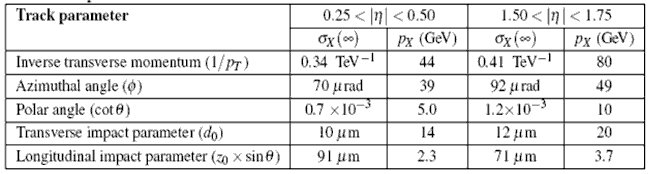
    Отметим, что сигналы TRT используются только для треков с |η| < 2,0.
    При измерении треков, в первую очередь лептонов, важно правильное определение знака электрического заряда. Для треков мюонов знак заряда определяется с достаточной точностью в мюонной системе до самых больших значений импульсов. Для электронов он может быть измерен лишь во Внутреннем детекторе. На рис.10.1 приведены вероятности ошибочного измерения заряда для мюонов и электронов с |η| < 2,5 в зависимости от их поперечного импульса (слева) и значения псевдобыстроты при р_т = 2 ТэВ (справа). Видно, что для электронов с р_т менее 1 ТэВ вероятность правильного определения заряда высока.
    Эффективности реконструкции треков различных частиц приведены на рис.10.2. Для пионов дополнительным эффектом, уменьшающим эффективность, кроме многократного рассеяния, служит взаимодействие с веществом детектора. Для электронов существенен дополнительный вклад тормозного излучения. Характер зависимости от псевдобыстроты отражает изменение количества вещества в детекторе. Электроны, выходя за пределы SCT, теряют в среднем от 20 до 50% своей энергии. Функцию идентификации электронов при импульсах до 25 ГэВ/с выполняет TRT.

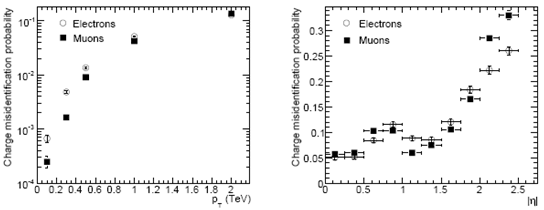Рис. 10.1 Вероятность ошибочного измерения заряда трека мюона и электрона в зависимости от поперечного импульса трека (слева) и псевдобыстроты для треков с рт = 2 ТэВ.

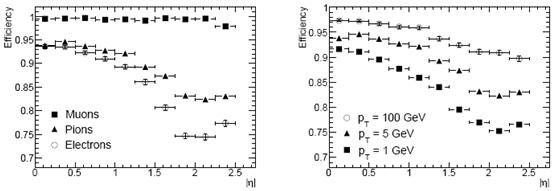Рис. 10.2. Эффективности реконструкции треков мюонов, пионов и электронов с рт = 5 ГэВ/с (слева) и треков пионов с рт = 1, 5 и 100 ГэВ/с.

    Величины относительного разрешения при измерении поперечных импульсов мюонов в зависимости от псевдобыстроты частицы показаны на рис. 10.3.

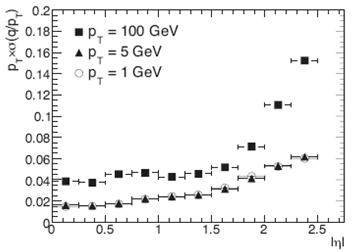Рис.10.3. Относительное разрешение при измерении поперечных импульсов мюонов при значениях рт = 1, 5 и 100 ГэВ/с в зависимости от псевдобыстроты частицы.

    Важной характеристикой является точность восстановления координаты точки соударения протонов, найденной по трекам вторичных частиц. На рис.10.4 показаны распределения первичных вершин взаимодействий для событий разных типов в поперечной плоскости и по оси пучка.

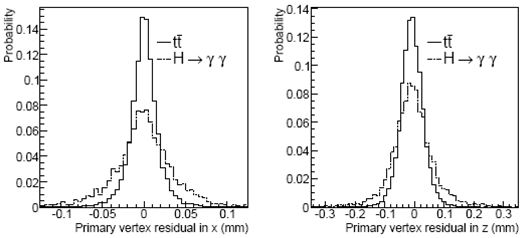Рис.10.4. Разрешение восстановление координат точки соударения протонов в событиях с рождением пары топ-кварков и бозона Хиггса, распадающегося на два фотона: по переменной х в поперечной плоскости (слева) и по продольной переменной z в мм.

    Измерение поперечного импульса мюонов по величине прогиба траектории в мюонном спектрометре зависит от точности камер и знания их относительного положения (выстроенности детектора). Разрешение этих измерений показано на рис.10.5. Детектор оптимизирован для мюонов с р_т ~ 100 ГэВ/с. При меньших импульсах одиночных мюонов результаты хуже за счет флюктуаций потерь в калориметре, при больших - за счет разрешения камер MDT. Для объединенных треков при малых р_т разрешение определяется Внутренним детектором, где при р_т менее 10 ГэВ/с доминирует вклад многократного рассеяния.

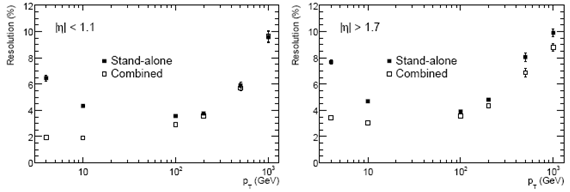Рис.10.5. Разрешение в % при измерении импульсов одиночных мюонов в мюоном спектрометре (stand-alone) и при объединении данных спектрометра и Внутреннего детектора (combined) для центральной |η| < 1,1(слева) и передней |η| > 1,7 областей.

Измерение энергии электронов и фотонов

    Разрешение при измерении энергии электронов и фотонов показано на рис. 10.6.

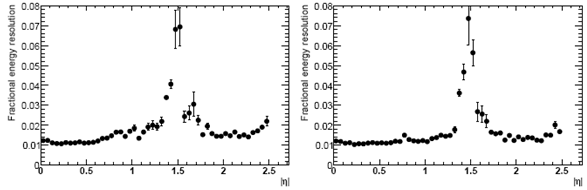Рис.10.6. Разрешение при измерении энергии электронов и фотонов с энергией 100 ГэВ в зависимости от их псевдобыстроты.

    Величина разрешения определяется степенью структурированности ЕМ калориметра и качеством его калибровки. Область ухудшения разрешения при |η| = 1,5 соответствует переходу от барреля к торцевой части и исключается при проведении анализа данных. Зависимость разрешения от энергии электронов и фотонов показана на рис. 10.7 для разных значений псевдобыстроты.

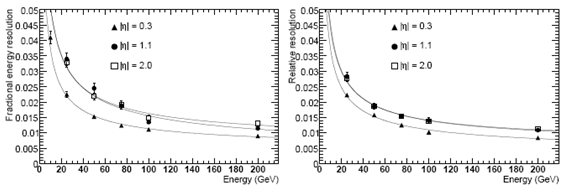Рис.10.7. Зависимость разрешения при измерении энергии от величины энергии электронов (слева) и фотонов при значениях псевдобыстроты |η| = 0,3, 1,1 и 2,0.

Реконструкция струй

    Реконструкция струй использует высокую степень структурированности калориметров ATLAS. Программное обеспечение позволяет применять различные алгоритмы выделения струй и работать с любыми входными объектами, характеризуемыми четырех–импульсами. Два основных алгоритма реконструкции – 1) с фиксированным конусом и 2) с последовательной рекомбинацией. Оба алгоритма используются в двух конфигурациях. В первом случае для выделения узких струй при исследовании спектроскопии W или t-рождения, а также кандидатов в события суперсимметрии с большим количеством струй. Во втором случае для выделения широких струй при исследовании КХД-процессов, двухструйного рождения и множественного образования струй при светимости
≤ 10³³см^-2 с^-1. Конусный алгоритм использует два параметра: пороговую поперечную энергию в начальной ячейке Е_т = 1 ГэВ и раствор конуса ΔR = 0,4 для поиска узких струй и 0,7 для поиска широких. Величина ΔR = √((Δη)² + (Δφ)²). В обоих случаях применяется расщепление и объединение струй при пороге на их перекрытие в 50%. Может использоваться также версия к_т алгоритма реконструкции струй. Конусный алгоритм вследствие своего быстродействия используется также в триггере высокого уровня.
    Все измерения в ячейках калориметра калибруются с использованием весовых функций, зависящих от геометрии и положения ячейки и уровня шумов. Основными требованиями к сигналам от струй после калибровки является линейная зависимость отклика калориметра от энергии струи во всем измеряемом диапазоне энергий, однородность отклика в зависимости от направления струи и стандартное разрешение. Линейность отклика калориметра демонстрируется на рис.10.8(а) для двух интервалов псевдобыстроты показаны величины: отношение энергии, измеренной в калориметре, к истинной энергии струи, нижние точки до калибровки, верхние после глобальной калибровки.

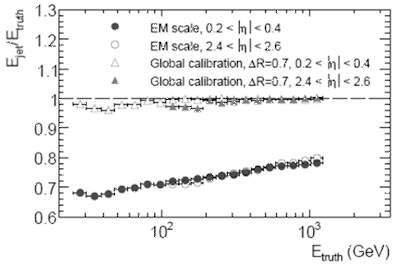Рис.10.8.(а) Линейность расчетного отклика калориметра в зависимости от энергии струи Еtruth.

Однородность углового отклика в двух интервалах поперечных энергий струй Е_т для конусных алгоритмов с ΔR = 0,4 и 0,7 показана на рис.10.8(б). Нарушения однородности в двух переходных областях по |η| более заметны при меньших энергиях струй.

Рис.10.8(б). Однородность углового отклика в двух интервалах поперечных энергий струй Ет для конусных алгоритмов с ΔR = 0,4 и 0,7.

На рис.10.8(в) приведено разрешение по энергии струй в зависимости от теоретического значения псевдобыстроты (или угла) струи |η|. Все результаты получены для процесса рождения двух КХД струй.

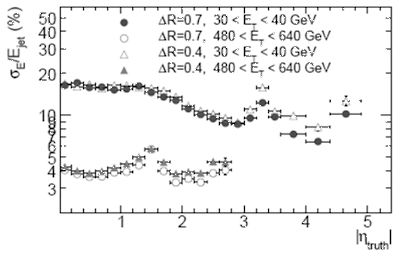Рис.10.8(в) Разрешение по энергии струй в зависимости от угла |η|.

    Кроме представленных параметров, качество реконструкции струй определяется дополнительными требованиями, предъявляемыми в процессе физического анализа. К ним относятся эффективность выделения струй, чистота набора, применимость вето и определение типа струи, ее принадлежности тому или иному физическому объекту. Определяются эти параметры для конкретных физических процессов.
    На рис.10.9 для примера показана эффективность реконструкции струй для двух алгоритмов в процессе рождения бозона Хиггса через механизм слияния векторных бозонов в зависимости от расчетной поперечной энергии струи р_т. Распад бозона Хиггса с массой 120 ГэВ происходит на два τ-лептона. Видно, что для струй с р_т выше 40 ГэВ оба алгоритма дают близкие результаты. Для меньших энергий их эффективность отличается. При малых энергиях ( > 10 ГэВ) примесь ложных струй велика и составляет в центральной области, например, 30% – 45% для указанных алгоритмов.

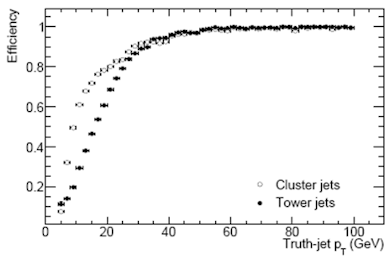Рис.10.9. Эффективность реконструкции струй для двух конусных алгоритмов с ΔR = 0,7 в процессе рождения бозона Хиггса через механизм слияния векторных бозонов в зависимости от расчетной поперечной энергии струи рт.

Измерение недостающей поперечной энергии

    При измерении недостающей поперечной энергии особую важность имеет линейность отклика калориметров. На рисунке 10.10 показана эта величина для распада бозона Хиггса с массой 800 ГэВ два τ-лептона.

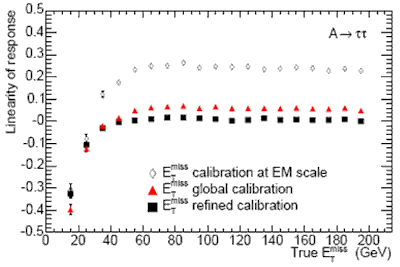Рис. 10.10. Линейность отклика калориметра при измерении недостающей поперечной энергии в процессе распада бозона Хиггса А на два τ-лептона.

    При измерении недостающей энергии особенно важна калибровка калориметра.
    Разрешение определения двух компонент вектора недостающей энергии в поперечной плоскости (х,y) в зависимости от суммарной измеренной поперечной энергии в калориметре ∑Е_т для разных физических процессов приведена на рис.10.11. Измерение компонент этого вектора дает возможность определить направление Е_тmiss. Для значений Е_тmiss выше примерно 100 ГэВ погрешность определения угла составляет 100 мрад. В некоторых случаях параметры Е_тmiss могут использоваться для вычисления эффективной массы объектов.
    Важной задачей при реконструкции струй является идентификация адронных распадов τ-лептонов. Они выделяются путем поиска узкого кластера энергии в калориметре, сопровождаемого малым количеством треков во Внутреннем детекторе. Другим способом идентификации струй является выделение струй b-кварков.

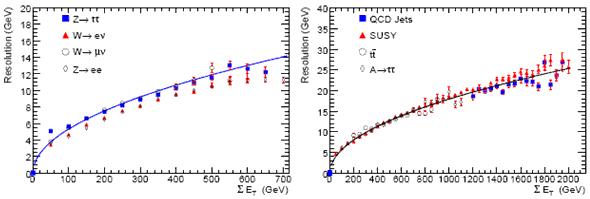Рис.10.11. Разрешение определения двух компонент вектора недостающей энергии в поперечной плоскости (х,y) в зависимости от суммарной измеренной поперечной энергии в калориметре ∑Ет для разных физических процессов.

Идентификация струй b-кварков

    Возможность идентификации адронных струй тяжелых кварков необходима для изучения многих процессов: рождения t-кварков, поиска бозона Хиггса и новой физики вне Стандартной модели. Струи реконструируются в калориметре стандартными алгоритмами. Рассматриваются в качестве кандидатов в струи b-кварков струи с р_т > 15 ГэВ и |η| < 2,5. Треки во Внутреннем детекторе относятся к струе, если их расстояние от оси струи R < 0,4. Не учитываются наложения событий. В расчетах модели кварк b или с (или τ-лептон) считается относящимся к струе, если его поперечный импульс более 5 ГэВ/с и он отстоит от оси струи на ΔR < 0,3. Это условие отбирает преимущественно струи b-кварков от процесса расщепления глюона на два b-кварка в партонном ливне. Среди треков струи отбираются надежно измеренные треки с р_т > 1 ГэВ и вычисляется их поперечный прицельный параметр d0 относительно точки соударения протонов. Величина d0 определяется как наименьшее расстояние от трека до точки взаимодействия и ей приписывается знак в зависимости от направления смещения относительно оси струи, определенной в калориметре. Если трек пересекает ось струи позади точки соударения, то величина d0 имеет отрицательный знак. На рис. 10.12 показаны распределения параметра d0 (|d0| < 1 мм) для треков от разных кварковых струй. Наибольшие положительные значения d0 присутствуют в струях b-кварков, наименьшие в струях от легких кварков u ,d, s.

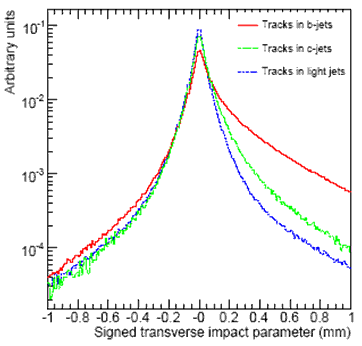Рис.10.12. Распределения параметра d0 с приписанным знаком для треков от разных кварковых струй.

    Повышение надежности идентификации проводится затем путем поиска вершины от распада В-адрона в струе, включая распад с-кварка, возникшего от распада В-адрона. Для этого комбинируются пары треков с наибольшими значениями прицельного параметра d0 и реконструируется их общая вершина. Для вершин с хорошим качеством реконструкции определяется эффективная масса частиц, чтобы исключить распады К⁰ и Λ-частиц и конверсии фотонов. Оставшиеся вершины объединяются в одну; определяется эффективная масса частиц в вершине и отношение суммарной энергии частиц в вершине к энергии всех частиц в струе, а также полное количество вершин с парами треков. Поведение этих трех параметров показано на рис.10.13 для струй b-кварков и легких струй.

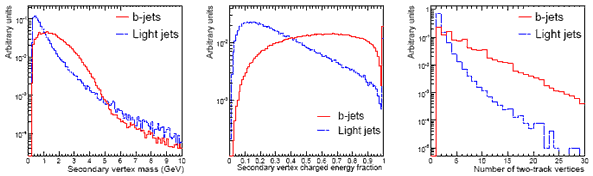Рис.10.13. Эффективная масса частиц из вторичной вершины в струе (справа), доля энергии струи, уносимая этими частицами, и количество двух частичных вершин в струе (слева). Сплошные линии соответствуют струям b-кварков, пунктирные – струям от легких кварков.

    Эффективность второго алгоритма зависит от топологии события. С применением обоих алгоритмов вычисляются функции максимального правдоподобия и используется многопараметрический анализ для оптимизации фактора подавления струй легких кварков и идентификации b-струй. Достигнутые соотношения степени подавления легких струй и эффективности выделения b-струй показаны на рис.10.14 для событий с рождением t и WH. Видно, что фактор подавления более 100 достижим при эффективности выделения b-струй 60%.

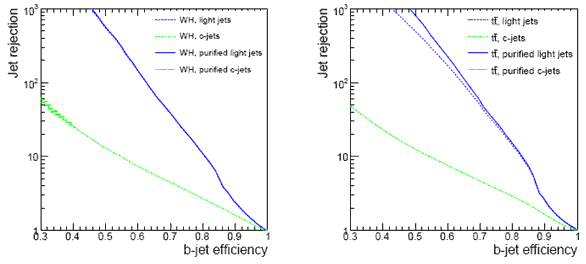Рис.10.14. Соотношение степени подавления легких струй и эффективности выделения b-струй для событий с рождением t (справа) и WH (слева).

    Коэффициент подавления струй легких кварков зависит от р_т струи и её псевдобыстроты. Это видно из рис.10.15.

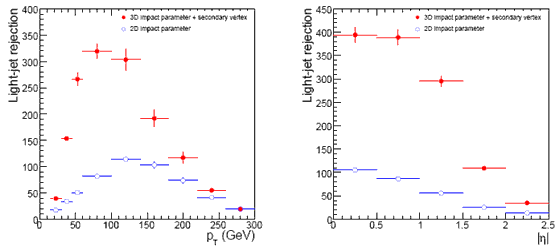Рис.10.15. Коэффициент подавления (режекции) струй легких кварков в зависимости от рт струи (слева) и псевдобыстроты. Разные точки отвечают алгоритмам в двухмерном пространстве прицельного параметра (светлые точки) и в трехмерном пространстве (темные точки).

    Наибольший интерес представляют оценки возможностей детектора для достижения основных задач LHC: поиска бозона Хиггса, суперсимметричных частиц и возможных экзотических состояний. Результаты моделирования потенциальных возможностей детектора ATLAS в наиболее актуальных областях физики частиц приведены в следующих разделах.